 |
Синтез структурных схем исполнительных механизмов
|
|
|
|
Синтез основных структурных схем. При проектировании промышленных роботов задача структурного синтеза исполнительного механизма, включающая выбор числа звеньев, числа, класса и порядка расположения кинематических пар, является одной из основных, так как ее решение связано непосредственно с выполнением функций промышленного робота. Синтез структурных схем исполнительного механизма проводят с использованием структурных формул. Число подвижных звеньев и кинематических пар пространственных исполнительных механизмов, удовлетворяющих требуемому (заданному) числу степеней подвижности и виду кинематических пар находят, по формуле:
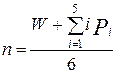 (5)
(5)
Следует отметить, что в результате расчетов число звеньев и кинематических пар должно быть целым.
В таблице 3 представлены сочетания чисел звеньев и кинематических пар разных классов, позволяющие синтезировать основные структурные схемы исполнительных механизмов в зависимости от их числа степеней подвижности.
Таблица 3 – Сочетания чисел звеньев и кинематических пар основных структурных схем

Примеры синтезированных основных структурных схем пространственных исполнительных механизмов приведены на рис. 3, а-ж.
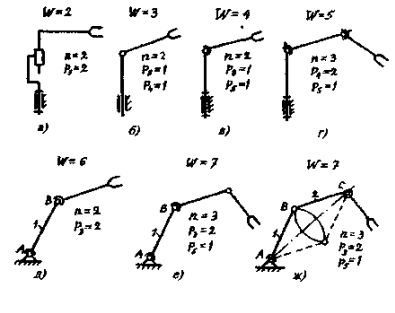
Рис.3
Структурные схемы (рис. 3,д,е) не рациональны, так как допускают вращение звеньев 1 вокруг своих продольных осей АВ (местная подвижность), что ни как не отражается на функциональных возможностях исполнительных механизмов, хотя и требует установки приводов для осуществления этих движений.
Структурная схема (рис. 3,ж) рациональна, так как допускает групповую подвижность звеньев 1 и 2 вокруг оси АС, что улучшает функциональные возможности исполнительного механизма (например, обход препятствий).
|
|
|
Так как в исполнительных механизмах промышленных роботов используют в основном кинематические пары 5-го класса, то число подвижных звеньев и кинематических пар пространственных структурных схем находят соответственно по формулам:
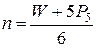 (6)
(6)
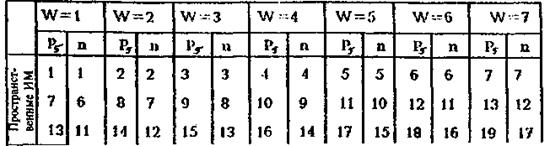
В табл. 4 представлены сочетания чисел звеньев и кинематических пар 5-го класса, позволяющие синтезировать структурные схемы исполнительных механизмов в зависимости от их числа степеней подвижности.
Таблица 4 – Сочетания чисел звеньев и кинематических пар 5-го класса структурных схем исполнительных механизмов.
Синтез основных структурных схем при помощи структурных групп. Структурная схема пространственного исполнительного механизма с шестью степенями подвижности может быть получена присоединением к рабочему органу групп звеньев с нулевой степенью подвижности (структурных групп), т.е. Wгр =0
При этом кинематическая цепь звеньев, соединяющая рабочий орган со стойкой, не должна изменять числа его степеней подвижности. Следовательно, эта кинематическая цепь также должна обладать нулевой степенью подвижности:
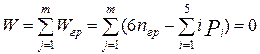 ,
,
где nгр – число подвижных звеньев структурной группы; m - число структурных групп.
Откуда можно найти число подвижных звеньев и кинематических пар пространственной структурной группы:
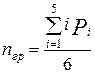 (7)
(7)
В частном случае для пространственных исполнительных механизмов с кинематическими парами 5-го класса:
 (8)
(8)
Пример 1. Синтезировать пространственную структурную схему исполнительного механизма с 6 степенями подвижности при помощи структурной группы, содержащей кинематические пары четвертого и пятого классов.
Определяем минимальное число звеньев и требуемых кинематических пар группы:
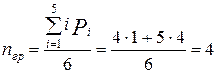
Структурная группа должна содержать 4 звена, 1 пару четвертого класса и 4 пары пятого класса. Строим структурную схему исполнительного механизма (рис.4).
|
|
|
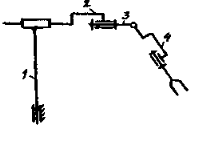
Рис. 4
Проверяем подвижность построенной структурной группы:
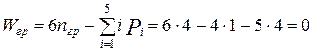
Вычисляем число степеней подвижности структурной схемы:

Синтезирована структурная схема исполнительного механизма по заданным условиям.
Построение основных структурных схем. Для обеспечения рабочему органу возможности занимать любое положение в пространстве, кинематическая цепь звеньев, соединяющая рабочий орган со стойкой, должна предоставить ему шесть степеней подвижности.
Большое число степеней подвижности, возможность в широких пределах варьировать сочетанием различных кинематических пар существенно затрудняет построение основных структурных схем исполнительных механизмов. Поэтому необходимо систематизировать движения звеньев в зависимости от их функционального назначения.
Три транспортирующие движения, осуществляющие только перемещения рабочего органа в пространстве, можно представить в виде двух элементарных групп движений:
группа В – вывод рабочего органа в любую точку плоскости (осуществляют с помощью двух звеньев 2 и 3 и двух кинематических пар II и III, табл. 5). Возможны 4 вида соединения звеньев;
группа А – поворот или перемещение этой плоскости (осуществляют с помощью одного звена 1 и одной кинематической пары I, табл. 5).
Три угловых движения, осуществляющих пространственную ориентацию рабочего органа, можно также представить в виде двух элементарных групп движений:
группа С – сферическое движение рабочего органа относительно точки (осуществляют с помощью двух звеньев 4 и 5 и двух кинематических пар IV и V 5-го класса, табл. 5);
группа Д – вращение (ротация) рабочего органа 6 относительно своей продольной оси (осуществляют с помощью одной вращательной кинематической пары VI 5-го класса, табл. 5).
Таблица 5 – Группы движений звеньев исполнительного механизма
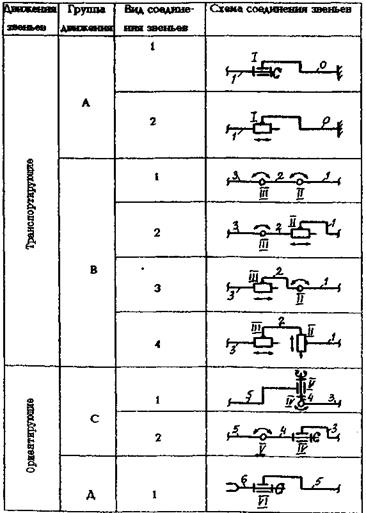
Основная структурная схема (ОСС) исполнительного механизма может быть получена соединением элементарных групп в следующей последовательности:
ОСС=A i +B j +C k +D
где i, j, k – номер вида элементарной структурной группы А, В, С соответственно.
Пример 2. Синтезировать основную пространственную структурную схему исполнительного механизма ПР с 6 степенями подвижности по следующим данным: i= l, j= l, k =2.
|
|
|
Строим основную структурную схему путем соединения элементарных групп в следующей последовательности (рис.5)

Рис.5
ОСС=A i +B j +C k +D= A 1 +B 1 +C 2 +D.
Вычисляем число степеней подвижности исполнительного механизма:

Число степеней подвижности структурной группы, соединяющей рабочий орган со стойкой:

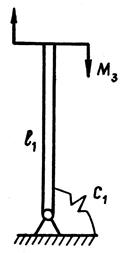
Параметры сечения руки с массой груза на конце т0 = 0,1 кг определим по схеме на рис.4а, полагая для простоты руку однородной и прямолинейной, а силу тяжести звена сосредоточенной в его центре.
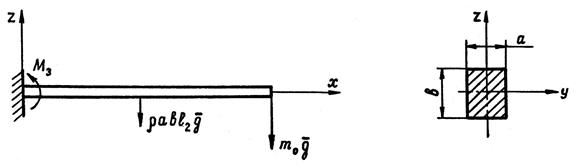
а)
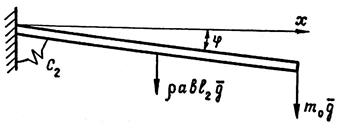
б) в)
Рис.4. Схема жесткостного синтеза звеньев МС:
а,б – руки; в – стойки
В силу линейности используемой теории деформируемой балки решение задачи изгиба можно вести посредством суперпозиции перемещений W1 , W2 в точках оси х от двух сосредоточенных в них сил:

В схеме с сосредоточенной жесткостью (рис.4б) этим двум значениям перемещений соответствуют различные углы поворота звена вокруг оси Оу:
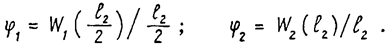
Тогда суммарный угол составляет величину:
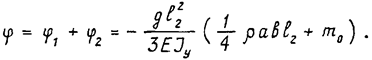
Жесткость руки будет достаточна, если ½ j ½ £e2 или:
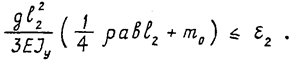
Принимая для определенности b = 2 а, получаем, что минимальное значение а, обеспечивающее требуемую жесткость руки, может быть найдено из уравнения:

Подставляя для стали r = 7800 кг*м-3, Е = 2,1.1011 Н*м-2, имеем а ³6,6 мм. Принимаем a = 7 мм, b = 14 мм. Эти размеры сечения звена хорошо согласуются с действительными. Следовательно, жесткость руки робота «Ритм-01.01» на изгиб можно считать достаточной.
Коэффициент жесткости С2 (рис.4б) может быть рассчитан из соотношения:

где М3 – момент заделки балки на рис.4а.
В нашем случае величина М3 равна:

Для оценки минимального коэффициента жесткости С1 (рис.2) обратимся к расчетной схеме на рис.4в, в соответствии с которой
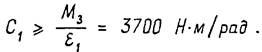
Сравнивая требуемое для обеспечения заданной точности значение коэффициента жесткости С1, с его действительным значением С1 = 300 Н*м/рад, приходим к выводу, о том, что податливость модуля поперечного сдвига ПР «Ритм-01.01» чрезвычайно велика. Для обеспечения достаточных в функциональном смысле точностных показателей ПР должна быть произведена существенная доработка конструкции этого узла в плане придания ей более высоких жесткостных свойств.
|
|
|
|
|
|


