 |
Запись ик-лазерного сигнала на уровне нелинейной динамики ДНК
|
|
|
|
Общая посылка данной части работы заключается в том, что хромосомный аппарат и его главная часть ДНК генерируют знаковые волновые структуры. Вместе с тем, геном способен на основе такого рода волновой памяти распознавать и корректировать пространственно-временную структуру биосистемы. Необходим простой и однозначный экспериментальный результат, который показал бы, что молекулы ДНК в принципе способны к памяти на внешнее электромагнитное поле. В качестве такового был выбран ИК-лазерный сигнал с учетом того, что ДНК in vivo оперирует таким излучением. Мы поставили несколько серий экспериментов для того, чтобы ввести in vitro такой искусственный лазерный сигнал в гель молекул ДНК с последующим анализом их нелинейной динамики как системы отображения ИК-лазерного воздействия на уровне явления возврата Ферми-Паста-Улама (ФПУ) [25]. Для введения такого рода сигнала в нелинейно-динамический континуум геля ДНК мы использовали импульсный режим работы ИК-лазера Ga-As с длиной волны 890 нм, частотой повторения импульсов 600 Гц со средней мощностью (минимум 0,8; максимум 3,1) Вт с временем однократной экспозиции 4 сек. Регистрацию воздействий лазера и подготовку образцов ДНК из эритроцитов кур вели в соответствии с [25], в частности, с использованием метода корреляционной лазерной спектроскопии. Анализ поведения временных автокорреляционных функций (АКФ) светорассеяния ДНК показал, что сигнал ИК-лазера запоминается биополимером в форме периодической стохастизации АКФ и носит долговременный и устойчивый характер. Периодические повторы стохастических АКФ допустимо трактовать как одну из форм явления возврата Ферми-Паста-Улама, сочетанного со свойственной этому явлению памятью. Замораживание ДНК геля в течение недели не влияет на приобретенную память на ИК-лазерный сигнал. После размораживания периодическая стохастизация АКФ данного препарата сохраняется, если поддерживать препарат в высокополимерной форме. Таким образом, удалось впервые осуществить запись внешнего искусственного импульсного ИК-лазерного воздействия на уровне нелинейной динамики ДНК, что может служить простейшей реалистической моделью эпигеноволновых процессов in vivo.
|
|
|
О ВОЗМОЖНОСТИ СОЗДАНИЯ ЛАЗЕРА НА ИНФОРМАЦИОННЫХ БИОМАКРОМОЛЕКУЛАХ [30]
Прошло несколько десятилетий после того, как лауреаты Нобелевской премии академики РАН А.Н.Прохоров, Н.Г.Басов (Россия) и Чарльз Таунс (США), высказали идею, а затем реализовали ее, о возможности создания квантовых генераторов. Сейчас трудно сказать, в какой области науки и техники они не применяются (от биологии и медицины до лазерного термоядерного синтеза). Последующие исследователи внесли свой крупный вклад в развитие этой проблемы.
В данной части работы ставится вопрос: можно ли in vitro создать лазер на информационных биомакромолекулах, прежде всего на ДНК, РНК и хромосомах? Вряд ли может идти речь о создании энергетически мощных лазеров на этих структурах. Вопрос звучит по-иному: какие новые знания мы можем получить о ДНК, РНК и хромосомах, создав такой лазер и исследуя характер его излучения? Можно думать, что это будут принципиально новые данные. Например, об их нелинейной динамике, в том числе солитонного типа, о ровибронных колебаниях, о модуляциях дисперсии оптического вращения и кругового дихроизма, переносе энергии в другие, ранее недоступные (в таком варианте методологии) слои информации. При этом динамические модификации лазерного пучка могут иметь cемантико-гено-биознаковый характер и поэтому будут обладать мощной биологической активностью.
|
|
|
Первые соображения по этому поводу были предложены нами ранее [25,30]. В том числе обсуждалась идея о создании лазерной системы на Фрёлиховских модах [3]. Сложность доказательства правильности всех этих мыслей состоит в том, что большинство генетических структур, содержащих в своем составе ароматические и гетероциклические кольца, “прозрачны” для характерного спектрального диапазона l @ 350-400нм. Трудность также и в том, что если использовать мощную оптическую накачку, то это, учитывая “хрупкость” биоструктур, неизбежно приведёт к их разрушению.
В настоящей главе для реализации некоторых из обсуждавшихся положений проведено исследование in vitro спектров двухфотонно-возбуждаемой люминесценции (ДВЛ) геле-жидкокристаллических препаратов нуклеогистона, являющегося суммарной фракцией хромосом, в которой преобладают гистоновые белки, и ДНК (стандартные высокополимерные препараты фирмы “Sigma”). Для существенного увеличечения интенсивности ДВЛ генетических структур нами предложен способ активации люминесценции за счет введения в состав исследуемых образцов активаторов (доноров) ДВЛ-определенных (близких по спектру оптического поглощения ДНК и нуклеогистону) органических молекул. Такие молекулы характеризуются большой интенсивностью спектров излучения, которые располагаются в области собственного оптического поглощения ДНК и нуклеогистона. В качестве активатора мы использовали кристаллический препарат димедрола, структура которого включает пару бензольных колец. Для димедрола это обеспечивает интенсивный спектр ДВЛ, имеющий вид широкой асимметричной полосы в диапазне 280 - 350нм.
Для фотонной накачки исследуемых препаратов мы применяли лазер на парах меди. Этот лазер работает в стандартном импульсно-периодическом режиме с частотой следования импульсов 10кГц, со средней мощностью  Вт, пиковой мощностью 10
Вт, пиковой мощностью 10  Вт, длинами волн генерации l = 510,8нм и 578,2нм (зеленая и желтая линии), длительностью импульсов
Вт, длинами волн генерации l = 510,8нм и 578,2нм (зеленая и желтая линии), длительностью импульсов 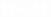 нс. Лазерное излучение направляли на исследуемый образец в виде сфокусированного пятна размером
нс. Лазерное излучение направляли на исследуемый образец в виде сфокусированного пятна размером  мм. Применение такого лазера как инициатора ДВЛ оказалось весьма эффективным при изучении электронно-колебательных спектров белков, ДНК, нуклеогистона и их компонентов (пурины, пиримидины, аминокислоты [19,30]). Регистрирующая аппаратура включала: фильтр для выделения лазерных линий с l =510,8 и 578,2 нм, фильтр для выделения излучений люминесценции в УФ и фиолетовом диапазонах (с подавлением лазерного излучения), монохроматор (тип МДР-2) для сканирования спектра в широком интервале (от УФ до видимой области), двухкоординатный самописец для регистрации спектров, измеритель для контроля опорного сигнала и определения эффективности наблюдаемого сигнала. Для подавления тепловых шумов применяли строб-импульс длительностью 25-30нс, синхронизированный с импульсом возбуждения. Регистрацию вторичного импульса излучения проводили с ФЭУ-130. Исследования спектров ДВЛ геле-жидкокристаллического препарата ДНК в смеси с димедролом (ДНК-ДЛ) и нуклеогистона с димедролом (НГ-ДЛ) показали, что амплитуда ДВЛ спектра ДНК-ДЛ лишь на порядок меньше таковой спектра ДВЛ чистого димедрола. Это обеспечивает существенное увеличение интенсивности ДВЛ смеси ДНК-ДЛ по сравнению с чистым препаратом ДНК в форме жесткого геля [19]. На этом же спектре обнаруживается ряд дополнительных особенностей изучаемых смесей. Оказалось, что квантовый выход ДВЛ для смеси НГ-ДЛ ниже, чем для смеси ДНК-ДЛ. Другая характерная черта - разгорание или тушение ДВЛ во времени. Для НГ-ДЛ наблюдается нарастание ДВЛ во времени. Обратный эффект наблюдается в случае ДНК-ДЛ. Представляет интерес присутствие вибронной структуры в спектрах ДВЛ в виде отдельных перекрывающихся полос в области 310-370 нм, особенно для ДНК-ДЛ. Такая структура близка к ранее наблюдавшимся спектрам ДВЛ для нуклеозид-трифосфатов [19].
мм. Применение такого лазера как инициатора ДВЛ оказалось весьма эффективным при изучении электронно-колебательных спектров белков, ДНК, нуклеогистона и их компонентов (пурины, пиримидины, аминокислоты [19,30]). Регистрирующая аппаратура включала: фильтр для выделения лазерных линий с l =510,8 и 578,2 нм, фильтр для выделения излучений люминесценции в УФ и фиолетовом диапазонах (с подавлением лазерного излучения), монохроматор (тип МДР-2) для сканирования спектра в широком интервале (от УФ до видимой области), двухкоординатный самописец для регистрации спектров, измеритель для контроля опорного сигнала и определения эффективности наблюдаемого сигнала. Для подавления тепловых шумов применяли строб-импульс длительностью 25-30нс, синхронизированный с импульсом возбуждения. Регистрацию вторичного импульса излучения проводили с ФЭУ-130. Исследования спектров ДВЛ геле-жидкокристаллического препарата ДНК в смеси с димедролом (ДНК-ДЛ) и нуклеогистона с димедролом (НГ-ДЛ) показали, что амплитуда ДВЛ спектра ДНК-ДЛ лишь на порядок меньше таковой спектра ДВЛ чистого димедрола. Это обеспечивает существенное увеличение интенсивности ДВЛ смеси ДНК-ДЛ по сравнению с чистым препаратом ДНК в форме жесткого геля [19]. На этом же спектре обнаруживается ряд дополнительных особенностей изучаемых смесей. Оказалось, что квантовый выход ДВЛ для смеси НГ-ДЛ ниже, чем для смеси ДНК-ДЛ. Другая характерная черта - разгорание или тушение ДВЛ во времени. Для НГ-ДЛ наблюдается нарастание ДВЛ во времени. Обратный эффект наблюдается в случае ДНК-ДЛ. Представляет интерес присутствие вибронной структуры в спектрах ДВЛ в виде отдельных перекрывающихся полос в области 310-370 нм, особенно для ДНК-ДЛ. Такая структура близка к ранее наблюдавшимся спектрам ДВЛ для нуклеозид-трифосфатов [19].
|
|
|
Механизм резкого увеличения квантового выхода ДВЛ нуклеогистона и ДНК при наличии донор-активатора (димедрола) может быть объяснен быстрой квазирезонансной передачей энергии от возбужденных молекул димедрола к исследуемым геноструктурам. Наблюдаемая при этом тонкая многополосчатая структура ДВЛ спектров коррелирует с характером вибронных полос для ряда ароматических и гетероциклических соединений, включая чистые нуклеозид-трифосфаты и ДНК [19]. Возникновение такого рода дискретизации спектров можно трактовать переходом электронов биомакромолекул с электронного терма S1 на возбужденные колебательные уровни основного состояния S0. В связи с этим может быть реализована инверсная заселенность на переходах  при достаточном заселении терма
при достаточном заселении терма  .
.
|
|
|
Проведем оценки необходимой интенсивности  лазерного излучения для создания инверсии (суперфлуоресценции) в условиях проведенных опытов.
лазерного излучения для создания инверсии (суперфлуоресценции) в условиях проведенных опытов.
Условия инверсии записываются следующим образом:
 , (1)
, (1)
где  - плотность рабочих молекул в состоянии
- плотность рабочих молекул в состоянии  ,
,  - плотность молекул в состоянии
- плотность молекул в состоянии  ,
,  и
и  - соответствующие статистические веса квантовых уровней.
- соответствующие статистические веса квантовых уровней.
Плотность заселенности оценивается из соотношения
 , (2)
, (2)
где 
 - скорость заселения уровня
- скорость заселения уровня  ,
,  - скорость его распада за счет излучательного процесса и (или) безызлучательных процессов.
- скорость его распада за счет излучательного процесса и (или) безызлучательных процессов.
Для величины  имеем оценку:
имеем оценку:
 (3)
(3)
где W и  - энергия и длительность лазерного импульса,
- энергия и длительность лазерного импульса,  - эффективный объем среды, в котором реализуется двухфотонное поглощение (S - площадь поперечного сечения сфокусированного светового пучка, падающего на исследуемый образец,
- эффективный объем среды, в котором реализуется двухфотонное поглощение (S - площадь поперечного сечения сфокусированного светового пучка, падающего на исследуемый образец,  - эффективная длина проникновения излучения в образец),
- эффективная длина проникновения излучения в образец), 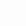 - плотность биомакромолекул (ДНК или нуклеогистона).
- плотность биомакромолекул (ДНК или нуклеогистона).
С учетом соотношений (1) - (3) условие для cоздания инверсной заселённости суперфлуоресценции записывается в виде
 .
.
Используя характерные данные

 (для
(для  нм) =
нм) =  Дж,
Дж,
t @ 10нс,  ,
, 
 ,
,
получаем оценку  ,
,
что близко к использованным значениям интенсивности в наших экспериментах.
Проведенные экспериментальные исследования и их теоретические оценки дают основание достаточно уверенно предполагать, что при используемых режимах двухфотонного возбуждения с использованием активатора-димедрола в геноструктурах in vitro реализуется усиление люминесценции, т.е. излучение ДНК и нуклеогистона носит характер суперфлуоресценции.
Не исключено, что в биосистеме роль димедролоподобных веществ в качестве активаторов могут выполнять эндогенные соединения, прямо или косвенно взаимодействующие с ДНК и хромосомами (стероидные гормоны, углеводы, нуклеозид -моно, -ди и -трифосфаты, некоторые витамины (например, рибофлавин), ароматические и гетероциклические аминокислоты, катехол- и индолалкиламины, некоторые антибиотики, наркотические вещества (например, эндогенные морфины - метаболиты этанола и пептиды-эндорфины), алкалоиды, токсины, ко-факторы ферментов, гем-содержащие белки и другие многочисленные органические соединения, содержащие бензольные и гетероциклические компоненты.
|
|
|
Неясны условия реализации инверсной электронной заселенности геноструктур in vivo, близкие тем, которые использовались нами в режимах ДВЛ. Такие условия могут создаваться в биосистемах, например, за счет фотон-фононных взаимодействий в ДНК в рамках теории Дике.
Однако, это относится к чисто физическим механизмам. Что касается физико-биохимических процессов, приводящих к лазерной накачке ДНК и хромосом in vivo, то в качестве таковых можно предсказать наличие в биосистемах мощных АТФ-азных систем, поставляющих энергию для перевода генетических структур в биокогерентные состояния (аналогичные тем, что как частный случай изложены в настоящей главе).
ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ ВОЗМОЖНОСТИ СОЗДАНИЯ БИОЛАЗЕРА НА ФРЕЛИХОВКИХ МОДАХ [3]
В данной главе обсуждается и аналитически рассматривается возможность создания перевозбужденного состояния основной (выделен-ной) коллективной Фрелиховской моды за счет когерентного резо-нансного взаимодействия электромагнитного (амплитудно-модулиро-ванного) излучения с Фрелиховским осциллятором. В рамках по-нятий лазерной физики речь идет о создании инверсной заселенности между квантовыми уровнями выделенной колебательной моды и, в итоге, о реализации “in vitro-in vivo” суперфлуоресценции и лазерной генерации с использованием в качестве рабочих тел молекул ДНК, РНК, белков, а также таких надмолекулярных структур, как рибосомы, полирибосомы и хромосомы.
Подчеркнем, что в отличие от Фрелиховского подхода, в котором подразумевается квазинеравновесное состояние (колебательная температура выделенной моды превосходит таковую “тепловой бани” Tvib>Teq>0, т.е. колебания квазиравновесны), в данной работе оценены условия, при которых система рассматриваемых биосубстратов инвертирована (Tvib<0), что прямо связано с созданием инверсной населенности.
Итак, Фрелиховская мода моделируется двухуровневой квантовой системой (уровень 1 - основное состояние, 2 - верхнее), возбуждаемой резонансным амплитудно-модулированным электрическим полем
E (t) =E og(t)сosw t, (1)
где E o - амплитуда напряженности поля, g(t) - модуляционный фактор, w =w 21 (w 21 - частота перехода 2® 1 ).
Процесс возбуждения колебаний моды описывается уравнением Больцмана для матрицы плотности:

 , (2)
, (2)
где оператор гамильтона в дипольном приближении имеет вид: 
где Ho=  w 21
w 21  - гамильтониан изолированной двухуровневой системы, оператору
- гамильтониан изолированной двухуровневой системы, оператору  соответствует матрица с элементами
соответствует матрица с элементами  11=
11=  12=
12=  21=0,
21=0,  22=1,
22=1,  - оператор прекции индуцированного дипольного момента осциллятора на направление поля,
- оператор прекции индуцированного дипольного момента осциллятора на направление поля, 
 - равновесная матрица плотности,
- равновесная матрица плотности,  - феноменологически введенное время релаксации (для диагональных элементов
- феноменологически введенное время релаксации (для диагональных элементов  =T1, для недиагональных - T2).
=T1, для недиагональных - T2).
Уравнению Больцмана (2) эквивалентна следующая система уравнений для элементов матрицы плотности ( ik; i,k=1,2):
ik; i,k=1,2):
i  (
( 11+(
11+( 11-1)/T1)= E(t)(
11-1)/T1)= E(t)( 21
21  12 -
12 -  12
12  21),
21),
i  (
( 12+
12+  12/T2)= -
12/T2)= - 
 21
21  12- E(t)
12- E(t)  12(
12( 22 -
22 -  11), (3)
11), (3)
i  (
( 21+
21+  21/T2)= +
21/T2)= + 
 21
21  21+E(t)
21+E(t)  21(
21( 22 -
22 -  11)
11)
с учетом уровня нормировки
 22+
22+  11=1 (4)
11=1 (4)
Нетрудно показать, что система (3) может сводиться к уравнению (при выкладках вторыми гармониками ~ exp(2i  21t) пренебрегалось):
21t) пренебрегалось):  22+
22+ 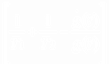
 22+
22+ 


 22 (0) =
22 (0) =  22 = 0, (5)
22 = 0, (5)
где  =Eo
=Eo  21/
21/  - частота Раби. Заметим, что амплитудная модуляция поля приводит не только к модуляциям частоы Раби, но и к модуляции “коэффициента трения” осциллятора.
- частота Раби. Заметим, что амплитудная модуляция поля приводит не только к модуляциям частоы Раби, но и к модуляции “коэффициента трения” осциллятора.
Ниже рассматривается случай T1=T2=T. Можно показать, что уравнение (5) допускает точное решение для произвольной функции g(t):
 (6)
(6)
G(t)= 

 (t’)dt’ (7)
(t’)dt’ (7)
Рассмотрим случай периодической модуляции амплитуды напряженности поля
g(t)=cos  t. (8)
t. (8)
Если период модуляции T  =2
=2 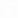 /
/  короче времени релаксации (T
короче времени релаксации (T  <<T), то для времени T
<<T), то для времени T  <<t<<T усреднение (6) за период T
<<t<<T усреднение (6) за период T  дает:
дает:
<  22>=1/2
22>=1/2 

 (9)
(9)
и, соответственно, (4):
<  11>=1/2
11>=1/2  ,
, 
где 
 - функция Бесселя нулевого порядка, так что для разности населенностей уровней 2 и 1 имеем
- функция Бесселя нулевого порядка, так что для разности населенностей уровней 2 и 1 имеем


 =
= 
 . (10)
. (10)
Из (10) четко следует, что в диапазонах параметра  , где k=1,2,.. и
, где k=1,2,.. и  - корни функции Бесселя, вероятность заселения уровня 2 превосходит таковую для уровня 1. Другими словами, мы имеем перевозбужденное инвертированное состояние осциллятора, что является необходимым условием для создания условий лазерной генерации (
- корни функции Бесселя, вероятность заселения уровня 2 превосходит таковую для уровня 1. Другими словами, мы имеем перевозбужденное инвертированное состояние осциллятора, что является необходимым условием для создания условий лазерной генерации ( ). Ситуация здесь аналогична процессу раскачивания маятника с пульсирующей точкой подвеса (маятник Капицы, классическое рассмотрение).
). Ситуация здесь аналогична процессу раскачивания маятника с пульсирующей точкой подвеса (маятник Капицы, классическое рассмотрение).
Для больших времен, t>>T, функция G(t), входящая в соотношение (6), имеет вид:
G(t)=P(t)cos  + Q(t)sin
+ Q(t)sin  ,
,
P(t)= 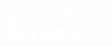

Q(t)=2  , (11)
, (11)
где J - функция Бесселя соответствующего порядка.
Из (11) следует важный вывод: когерентный механизм взаимодействия Фрелиховских мод с резонансным амплитудно-модулированным полем обусловливает незатухающие колебания диагональных элементов матрицы плотности для времен t, превосходящих времена релаксации системы, причем частоты пульсаций кратны частоте амплитудной модуляции  .
.
Усредняя (11) за период T  , получаем
, получаем
<G(t)>=  , (12)
, (12)
где x =  - функции Бесселя мнимого порядка (i - мнимая единица). В частном случае, когда период модуляции T
- функции Бесселя мнимого порядка (i - мнимая единица). В частном случае, когда период модуляции T 
 короче времени релаксации T, x <<1,
короче времени релаксации T, x <<1,
< 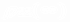 >=1/2
>=1/2 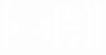 , <
, < 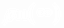 >=1/2
>=1/2  , (13)
, (13)
так что
<  > - <
> - <  >= -
>= -  . (14)
. (14)
В данном случае эффект инверсии не реализуется.
Рассмотрим случай, когда закон модуляции задается соотношением
g(t)=1+  . (15)
. (15)
По аналогии с предыдущим для функции G(t), входящей в соотношение (6), можно получить (T  .
.
G(t)=  . (16)
. (16)
Из (16) видно, что спектр пульсаций диагональных матричных элементов  и
и  включает, кроме частоты Раби, “стоксовые” и “антистоксовые” комбинационные частоты
включает, кроме частоты Раби, “стоксовые” и “антистоксовые” комбинационные частоты 
 . Допустим для определенных n выполнено условие
. Допустим для определенных n выполнено условие  , т.е.
, т.е.
 (17)
(17)
тогда, как следует из (16), постоянная составляющая для вероятностей  и
и  сдвигается. Динамическому состоянию равновесия при этом соответствуют величины:
сдвигается. Динамическому состоянию равновесия при этом соответствуют величины:
<  >=1/2
>=1/2  , <
, <  >=1/2
>=1/2  , (18)
, (18)
так что 
Эффект инверсии ( реализуется при условии
реализуется при условии
 . (19)
. (19)
Если параметр глубины модуляции  лежит в диапазонах, где значения функции Бесселя
лежит в диапазонах, где значения функции Бесселя  отрицательны, то реализуется режим перевозбуждения системы (информационных биомакромолекул и надмолекулярных структур).
отрицательны, то реализуется режим перевозбуждения системы (информационных биомакромолекул и надмолекулярных структур).
Таким образом, высказана идея принципиальной возможности создания биолазеров на Фрелиховских модах in vitro, а также инициации таких процессов в живой клетке в дополнение (или коррекции) к известным естественным лазероподобным процессам в биосистемах. Показано, что в определенных условиях - в случае когерентного (резо-нансного) взаимодействия амплитудно-модулированного внешнего электромагнитного излучения с Фрелиховской модой - система информационных биоструктур может существовать в перевозбужденном состоянии, что является необходимой предпосылкой для создания знаконесущих биолазеров.
Необходимо отметить,что описанный выше механизм формирования биолазеров на основе молекул ДНК позволяет подойти к попытке реализации еще одной фундаментальной гипотезы Фрелиха о возможности перекачки энергии kТ внутриклеточной жидкости в энергию электрических колебаний в молекуле ДНК. В соответствии с этой гипотезой стохастические тепловые колебания kТ раствора могут резонансно взаимодействовать (в определенном интервале частот) с колебательными модами молекулы ДНК, и благодаря тому, что как молекула ДНК, так и молекулы белков представляют собой распределенные нелинейные колебательные структуры, часть энергии может группироваться в низкочастотных модах этих молекул. Иными словами, молекула ДНК в растворе может частично преобразовывать энергию колебаний kТ в энергию собственных мод. Заметим, что даже в рамках предложенного квазили-нейного подхода проблема перекачки тепловой энергии раствора может быть сведена к механизму затухания квантового осциллятора, который был предложен А.Пиппардом. C учетом этого в уравнение Шредингера вводится комплексный потенциал, интерпретирующий передачу энергии осциллятора большому числу мод расширяющегося сферического резонатора. Если размеры этого резонатора конечны, как в случае с живой клеткой, то возникнет резонансный обмен энергии между модами kТ раствора и электрическими модами молекулы ДНК. Эти рассуждения также говорят в пользу того, что и в водно-жидкокристаллическом электролите клеточно-тканевого пространства биосистемы генетические молекулы могут функционировать как биолазеры.
Надо указать на существенное обстоятельство относительно принципиальной возможности реализации возбуждения Фрелиховских мод “in vitro” по биохимическому пути, а именно за счет энергии гидролиза АТФ и других нуклеозид-трифосфатов, а также за счет других макроэргических соединений живой клетки. В данном случае мы будем искусственно повторять то, что эволюционно и (или) иным путем дано биосистемам как основная информационная и, может быть, энергетическая фигура. Эта часть наших исследований ставит определенные нравственные и этические проблемы применения биолазеров.
АНТЕННАЯ МОДЕЛЬ ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ [16]
Как уже неоднократно отмечалось, функционирование ряда биологических макромолекул (в частности, ферментов) и других биологических соединений во многом определяется процессами, происходящими в активных центрах, окруженных биополимерными цепочками, имеющими знаковую топологию. Исходя из такого представления о структуре информационных биомакромолекул, естественно предположить, что их взаимодействие с физическими полями внешних по отношению к биосистеме и внутренних (организменных) излучений приводит к возбуждению дипольно-активных колебаний мономеров, формирующих указанную цепочку, а те, в свою очередь, индуцируют колебания в активном центре. Иными словами, такая система будет работать как своеобразная антенна. Эти возбужденные колебания способны привести к переходу биомакромолекулы в другое конформационное (топологическое, знаковое) состояние.
Подобная концепция в принципиальном плане адекватна целому ряду функционально высокозначимых биомакромолекул, например, хлорофилла, гемоглобина, миоглобина и т. д. Эти макромолекулы объединяются двумя структурными качествами: 1) в их геометрическом центре расположен ион (в случае хлорофилла - ион магния, в случае гемоглобина - ион железа); 2) около иона симметрично расположены 4 пиррольных кольца (псевдоплоская структура).
Другими типами биополимеров, соответствующих антенной модели, могут быть cравнительно простые циклы типа валиномицина (переносчик ионов калия) и сложные надмолекулярные структуры хромосом, ДНК которых содержит высокоорганизованные ассоциаты таких металлов, как магний, кальций, никель, кобальт, медь, железо, цинк и др. При этом роль их неясна и сводится исследователями, в основном, к нейтрализации ОН-групп остатков фосфорной кислоты полинуклеотида. Представляется, что функции металлов в ДНК и РНК существенно более широкие и реализуются по линии знакового и (или) энергетического взаимодействия с эндогенными и экзогенными по отношению к биосистеме физическими полями. То же относится и к белкам, не содержащим порфириновый центр, но специфическим образом связывающим металлы. Например, таковыми можно считать сайт-специфические белки с доменами типа “цинковых пальцев”, участвующими в регуляции генов, подчас очень далеко отстоящих от этих управляющих белков. Атомы металлов ДНК и белков могут резонансно взаимодействовать по электромагнитным каналам в рамках понятий антенной модели. Еще раз обозначим понятие антенной модели.
Внешняя энергия (в частности, связанная с резонансным взаимодействием крайне высокочастотных электромагнитных излучений с белками) поступает на периферию, т. е. на ансамбль субъединиц (не обязательно идентичных по структуре). В результате активной “беседы”, предопределенной биохимическими связями, между периферийными акцепторами (получившими закодированную энергию) и центром-ассоциатом (в данном случае ионом металла гемсодержащих белков), последний получает энергию (информацию), что и вызывает биологическое действие. Степень реакционной способности биомакромолекул существенно зависит от уровня возбуждения центральных субъединиц. Рассмотрим в деталях потенциальные механизмы волновых взаимодействий физических полей и активных центров информационных биомакромолекул в рамках предлагаемой нами антенной модели.
В качестве простейшей модели для иллюстрации антенного эффекта рассмотрим двумерную замкнутую (циклическую) цепочку мономеров. В центре цикла расположен активный центр, связанный с мономерами цепочки диполь-дипольным взаимодействием.
Обозначим координатные смещения мономеров через  , а смещение активного центра через
, а смещение активного центра через  . Для потенциальной функции имеем:
. Для потенциальной функции имеем:
 (1)
(1)
Первые два члена в (1) соответствуют колебаниям мономеров (второй член учитывает ангармонизм); последние два члена отвечают за связи между мономерами, Остальные члены отвечают за связи между мономерами и активным центром.
Уравнения движения запишем в виде:
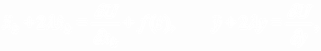 (2)
(2)
где  - внешняя монохроматическая сила, действующая только на мономеры,
- внешняя монохроматическая сила, действующая только на мономеры,  - коэффициент затухания, введенный феноменологически (простоты ради принят одинаковым и для мономеров, и для активного центра).
- коэффициент затухания, введенный феноменологически (простоты ради принят одинаковым и для мономеров, и для активного центра).
С учетом (1), система уравнений (2) приобретает вид:
 (3)
(3)
 (4)
(4)
Введем общую координату для ансамбля мономеров
 . (5)
. (5)
тогда система уравнений (4) в линейном приближении приобретает вид:
 (6)
(6)
где:

 - число мономеров.
- число мономеров.
С учетом (5) имеем  (7.1)
(7.1)
 (7.2)
(7.2)
Из (7.2) следует 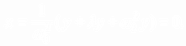 (8)
(8)
Подстановка (8) в (7.1) дает
 .
.
(9)
Соответствующее характеристическое уравнение имеет вид (после подстановки  в однородное уравнение):
в однородное уравнение):
 (10)
(10)
Обозначив  имеем
имеем

так что
 (11)
(11)
В дальнейшем предполагается выполнение неравенств:
 (12)
(12)
Первое условие соответствует случаю слабой связи между мономерами и активным центром, второе - малому затуханию мономерных осцилляторов.
Для собственных значений имеем
 , (13)
, (13)
где введены коллективные частоты:
 (14)
(14)
Нас интересуют вынужденные колебания (внешняя сила  ):
):
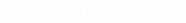 . (15)
. (15)
Подстановка (15) в (9) и приравнивание соответствующих коэффициентов при  и
и 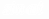 дают систему алгебраических уравнений:
дают систему алгебраических уравнений:

где:

В результате получаем 
где 
После несложных, но громоздких преобразований для вынужденных колебаний активного центра получаем:
 . (16)
. (16)
Из (16) видно, что наибольшая амплитуда вынужденных колебаний активного центра достигается в условиях коллективного резонанса: либо  , либо
, либо  .
.
В любом из этих случаев для амплитуды вынужденных колебаний имеем:
 (17)
(17)
Из (17) следует, что наибольший эффект резонансной раскачки активного центра достигается при большем числе периферийных субъединиц “антенны”, при более высоком значении коэффициента связи активного центра с мономерами, при наименьшем коэффициенте затухания и при наименьшем дисбалансе коллективных мод.
Нетрудно определить и “хореографию” (динамику вынужденных колебаний) отдельных мономерных единиц. В соответствии с (6) уравнение для k -го мономера запишем в виде:
 (18)
(18)
Вводя коллективные координаты

и применяя метод линейной алгебры, получаем для вынужденных колебаний мономеров:
 ,
,
(19)
где:

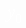 - определяется из (16)
- определяется из (16)
Таким образом, в рамках антенной модели наибольший эффект воздействия внешнего монохроматического поля  ре-ализуется в условиях коллективного резонанса:
ре-ализуется в условиях коллективного резонанса:
 .
.
Повторяя рассуждения раздела 2, можно сделать также следующие выводы:
1) При реализации амплитудной модуляции внешнего сигнала имеют место дополнительные возможности резонансного воздействия на биомакромолекулы на частотах:

2) Учет нелинейности при квадратичной связи для монохроматического сигнала привносит дополнительный резонанс на второй гармонике 
3) Учет нелинейности при амплитудной модуля
|
|
|


