 |
Оценка существенности параметров линейной модели.
|
|
|
|
Автокорреляция остатков.
Причины возникновения автокорреляции в эконометрических моделях
Понятие автокорреляции
Определение: Автокорреляция — это взаимосвязь последовательных элементов временного или пространственного ряда данных.
В эконометрических исследованиях часто возникают и такие ситуации, когда дисперсия остатков постоянная, но наблюдается их ковариация. Это явление называют автокорреляцией остатков.
Автокорреляция остатков чаще всего наблюдается тогда, когда эконометрическая модель строится на основе временных рядов. Если существует корреляция между последовательными значениями некоторой независимой переменной, то будет наблюдаться и корреляция последовательных значений остатков.
Автокорреляция может быть также следствием ошибочной спецификации эконометрической модели. Кроме того, наличие автокорреляции остатков может означать, что необходимо ввести в модель новую независимую переменную.
Проиллюстрируем проблему автокорреляции остатков на примере эконометрической модели с двумя переменными. Пусть
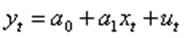 (1)
(1)
где мы предполагаем, что остатки ut, удовлетворяют схему авторегресии первого порядка, то есть зависят только от остатков предыдущего периода:
 (2)
(2)
для которой |ρ| < 1, а εt имеют такие свойства:
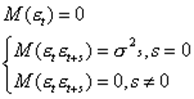
Величина ρ характеризует уровень взаимосвязи каждого следующего значения с предыдущим то есть ковариацию остатков.
Спецификация модели (1) имеет индекс t, что свидетельствует о ее динамическом характере, то есть и — период времени, для которого строится такая модель динамических (временных) рядов исходных данных.
Рассмотрим остатки модели ut, учитывая (2):

Отсюда
|
|
|
.  (3)
(3)
Поскольку:  , то.
, то. 
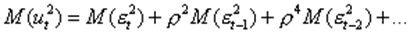
Учитывая, что последовательные значения, независимы, запишем
. 
Тогда
.  (4)
(4)
Ковариация последовательных значений остатков запишется в виде


и в общем случае
 (5)
(5)
то есть для модели (1) не удовлетворяется гипотеза о независимости последовательных значений остатков.
Выражение (5) можно записать так:
.  (6)
(6)
Это означает, что при наличии автокорреляции остатков второе необходимое условие подается в виде: 
где S - матрица коэффициентов автокорреляции s-го порядка для ряда ut,, или

.  (7)
(7)
Сравнив матрицу, которую имеем в данном случае, с матрицей при наличии гетероскедастичности, увидим, что они существенным образом отличаются одна от другой. Это связано с тем, как понимается второе условие для применения метода МНК при явлении гетероскедастичности и автокорреляции.
Итак, для гетероскедастичных остатков существует одна форма нарушения стандартной гипотезы, в соответствии с которой М(ии')=σ2u*S, для автокореляционных остатков мы сталкиваемся с второй формой нарушения этой гипотезы.
Оценка существенности параметров линейной модели.
7.1. Анализ вариации зависимой переменной в регрессии
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и, следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на две части – «объясненную» и «необъясненную».

 +
+  (7.1)
(7.1)
TSS RSS ESS
где
TSS – общая сумма квадратов отклонений;
|
|
|
RSS – сумма квадратов отклонений, объясненная регрессией;
ESS – остаточная сумма квадратов отклонений.
Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения у вызвана влиянием множества причин.
Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ОХ и среднее значение у равно оценке (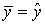 ). Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов (рис. 7.1).
). Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов (рис. 7.1).
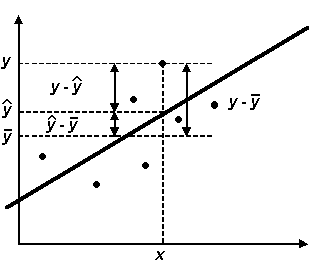
Рис.7.1
7.2. Коэффициент детерминации R2
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции R2= r2yx, называемый коэффициентом детерминации.
Коэффициент детерминации характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей регрессии результативного признака. Соответственно величина 1- r2 yx характеризует дисперсии У, вызванную влиянием остальных, не учтенных в моделях факторов. Величина коэффициента детерминации служит одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше меньше роль прочих факторов и, следовательно, линейная модель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза.
 (7.2)
(7.2)
Это равенство верно лишь в том случае, если верно (7.1), т.е. когда константа включена в уравнение регрессии. Только в этом случае имеет смысл рассматривать статистку R2. В силу определения R2 принимает значения между 0 и 1. Если коэффициент детерминации равен 0, то это означает, что регрессия ничего не дает, не улучшает качество предсказания у по сравнению с тривиальным предсказанием у среднее. Чем ближе к 1 значение R2, тем лучше качество подгонки, т.е точность аппроксимации.
|
|
|


