 |
Интервалы выпуклости и вогнутости функции
|
|
|
|
Возрастание и убывание функции
Решение различных задач из области математики, физики и техники приводит к установлению функциональной зависимости между участвующими в данном явлении переменными величинами.
Если такую функциональную зависимость можно выразить аналитически, то есть в виде одной или нескольких формул, то появляется возможность исследовать ее средствами математического анализа.
Имеется в виду возможность выяснения поведения функции при изменении той или иной переменной величины (где функция возрастает, где убывает, где достигает максимума и т.д.).
Применение дифференциального исчисления к исследованию функции опирается на весьма простую связь, существующую между поведением функции и свойствами ее производной, прежде всего ее первой и второй производной.
Рассмотрим, как можно находить интервалы возрастания или убывания функции, то есть интервалы ее монотонности. Исходя из определения монотонно убывающей и возрастающей функции, можно сформулировать теоремы, позволяющие связать значение первой производной данной функции с характером ее монотонности.
Теорема 1.1. Если функция y = f(x), дифференцируемая на интервале (a,b), монотонно возрастает на этом интервале, то в любой его точке
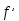 (x) >0; если она монотонно убывает, то в любой точке интервала
(x) >0; если она монотонно убывает, то в любой точке интервала 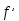 (x)<0.
(x)<0.
Доказательство. Пусть функция y = f(x) монотонно возрастает на (a,b), значит, для любого достаточно малого 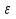 > 0 выполняется неравенство:
> 0 выполняется неравенство:
f (x- 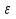 ) < f (x) < f (x+
) < f (x) < f (x+ 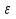 ) (рис. 1.1).
) (рис. 1.1).
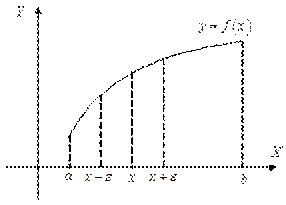
Рис. 1.1
Рассмотрим предел
 .
.
Если  > 0, то
> 0, то  > 0, если
> 0, если  < 0, то
< 0, то
 < 0.
< 0.
В обоих случаях выражение под знаком предела положительно, значит, и предел положителен, то есть 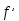 (x)>0, что и требовалось доказать. Аналогично доказывается и вторая часть теоремы, связанная с монотонным убыванием функции.
(x)>0, что и требовалось доказать. Аналогично доказывается и вторая часть теоремы, связанная с монотонным убыванием функции.
|
|
|
Теорема 1.2. Если функция y = f(x), непрерывна на отрезке [a,b] и дифференцируема во всех его внутренних точках, и, кроме того, 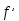 (x) >0 для любого x ϵ (a,b), то данная функция монотонно возрастает на (a,b); если
(x) >0 для любого x ϵ (a,b), то данная функция монотонно возрастает на (a,b); если
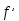 (x) <0 для любого xϵ (a,b), то данная функция монотонно убывает на (a,b).
(x) <0 для любого xϵ (a,b), то данная функция монотонно убывает на (a,b).
Доказательство. Возьмем  ϵ (a,b) и
ϵ (a,b) и 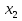 ϵ (a,b), причем
ϵ (a,b), причем  <
< 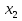 . По теореме Лагранжа
. По теореме Лагранжа
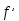 (c) =
(c) =  .
.
Но 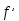 (c)>0 и
(c)>0 и 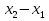 > 0, значит,
> 0, значит,  (
( > 0, то есть
> 0, то есть
 (
( . Полученный результат указывает на монотонное возрастание функции, что и требовалось доказать. Аналогично доказывается вторая часть теоремы.
. Полученный результат указывает на монотонное возрастание функции, что и требовалось доказать. Аналогично доказывается вторая часть теоремы.
Экстремумы функции
При исследовании поведения функции особую роль играют точки, которые отделяют друг от друга интервалы монотонного возрастания от интервалов ее монотонного убывания.
Определение 2.1. Точка  называется точкой максимума функции
называется точкой максимума функции
y = f(x), если для любого, сколь угодно малого  ,
,  (
( < 0, а точка
< 0, а точка 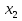 называется точкой минимума, если
называется точкой минимума, если  (
( > 0.
> 0.
Точки минимума и максимума имеют общее название точек экстремума. У кусочно-монотонной функции таких точек конечное число на конечном интервале (рис. 2.1).

Рис. 2.1
Теорема 2.1 (необходимое условие существования экстремума). Если дифференцируемая на интервале (a,b) функция имеет в точке  из этого интервала максимум, то ее производная в этой точке равна нулю. То же самое можно сказать и о точке минимума
из этого интервала максимум, то ее производная в этой точке равна нулю. То же самое можно сказать и о точке минимума 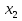 .
.
Доказательство этой теоремы следует из теоремы Ролля, в которой было показано, что в точках минимума или максимума  = 0, и касательная, проведенная к графику функции в этих точках, параллельна оси OX.
= 0, и касательная, проведенная к графику функции в этих точках, параллельна оси OX.
Из теоремы 2.1 вытекает, что если функция y = f(x) имеет производную во всех точках, то она может достигать экстремума в тех точках, где  = 0.
= 0.
Однако данное условие не является достаточным, так как существуют функции, у которых указанное условие выполняется, но экстремума нет. Например, у функции y =  в точке x = 0 производная равна нулю, однако экстремума в этой точке нет. Кроме того, экстремум может быть в тех точках, где производная не существует. Например, у функции y = |x| есть минимум в точке x = 0, хотя производная в этой точке не существует.
в точке x = 0 производная равна нулю, однако экстремума в этой точке нет. Кроме того, экстремум может быть в тех точках, где производная не существует. Например, у функции y = |x| есть минимум в точке x = 0, хотя производная в этой точке не существует.
|
|
|
Определение 2.2. Точки, в которых производная функции обращается в ноль или терпит разрыв, называются критическими точками данной функции.
Следовательно, теоремы 2.1 недостаточно для определения экстремальных точек.
Теорема 2.2 (достаточное условие существования экстремума). Пусть функция y = f(x) непрерывна на интервале (a,b), который содержит ее критическую точку  , и дифференцируема во всех точках этого интервала, за исключением, быть может, самой точки
, и дифференцируема во всех точках этого интервала, за исключением, быть может, самой точки  . Тогда, если при переходе этой точки слева направо знак производной меняется с плюса на минус, то это точка максимума, и, наоборот, с минуса на плюс – точка минимума.
. Тогда, если при переходе этой точки слева направо знак производной меняется с плюса на минус, то это точка максимума, и, наоборот, с минуса на плюс – точка минимума.
Доказательство. Если производная функции меняет свой знак при переходе точки  слева направо с плюса на минус, то функция переходит от возрастания к убыванию, то есть достигает в точке
слева направо с плюса на минус, то функция переходит от возрастания к убыванию, то есть достигает в точке  своего максимума и наоборот.
своего максимума и наоборот.
Из вышесказанного следует схема исследования функции на экстремум:
1) находят область определения функции;
2) вычисляют производную;
3) находят критические точки;
4) по изменению знака первой производной определяют их характер.
Не следует путать задачу исследования функции на экстремум с задачей определения минимального и максимального значения функции на отрезке. Во втором случае необходимо найти не только экстремальные точки на отрезке, но и сравнить их со значением функции на его концах.
Интервалы выпуклости и вогнутости функции
Еще одной характеристикой графика функции, которую можно определять с помощью производной, является его выпуклость или вогнутость.
Определение 3.1. Функция y = f(x) называется выпуклой на промежутке (a,b), если ее график расположен ниже любой касательной, проведенной к нему на данном промежутке, и наоборот, называется вогнутой, если ее график окажется выше любой касательной, проведенной к нему на данном промежутке.
Докажем теорему, позволяющую определять интервалы выпуклости и вогнутости функции.
|
|
|
Теорема 3.1. Если во всех точках интервала (a,b) вторая производная функции 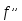 (x) непрерывна и отрицательна, то функция y = f(x) выпукла и наоборот, если вторая производная непрерывна и положительна, то функция вогнута.
(x) непрерывна и отрицательна, то функция y = f(x) выпукла и наоборот, если вторая производная непрерывна и положительна, то функция вогнута.
Доказательство проведем для интервала выпуклости функции. Возьмем произвольную точку  ϵ (a,b) и проведем в этой точке касательную к графику функции y = f(x) (рис. 3.1).
ϵ (a,b) и проведем в этой точке касательную к графику функции y = f(x) (рис. 3.1).
Теорема будет доказана, если будет показано, что все точки кривой на промежутке (a,b) лежат под этой касательной. Иначе говоря, необходимо доказать, что для одних и тех же значений x ординаты кривой y = f(x) меньше, чем ординаты касательной, проведенной к ней в точке  .
.

Рис. 3.1
Для определенности обозначим уравнение кривой:  = f(x), а уравнение касательной к ней в точке
= f(x), а уравнение касательной к ней в точке  :
:
 - f(
- f(  ) =
) = 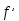 (
(  )(x-
)(x-  )
)
или
 = f(
= f(  ) +
) + 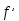 (
(  )(x-
)(x-  ).
).
Составим разность  и
и  :
:
 -
-  = f(x) – f(
= f(x) – f(  ) -
) - 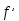 (
(  )(x-
)(x-  ).
).
Применим к разности f(x) – f(  ) теорему о среднем Лагранжа:
) теорему о среднем Лагранжа:
 -
-  =
= 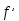 (
(  )(x-
)(x-  ) -
) - 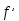 (
(  )(x-
)(x-  ) = (x-
) = (x-  )[
)[ 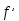 (
(  ) -
) - 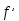 (
(  )],
)],
где  ϵ (
ϵ (  ,x).
,x).
Применим теперь теорему Лагранжа к выражению в квадратных скобках:
 -
-  =
= 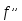 (
(  )(
)(  -
-  )(x-
)(x-  ), где
), где  ϵ (
ϵ (  ,
,  ).
).
Как видно из рисунка, x >  , тогда x -
, тогда x -  > 0 и
> 0 и  -
-  > 0. Кроме того, по условию теоремы,
> 0. Кроме того, по условию теоремы, 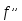 (
(  )<0.
)<0.
Перемножая эти три множителя, получим, что 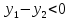 , что и требовалось доказать.
, что и требовалось доказать.
Определение 3.2. Точка, отделяющая интервал выпуклости от интервала вогнутости, называется точкой перегиба.
Из определения 3.1 следует, что в данной точке касательная пересекает кривую, то есть с одной стороны кривая расположена ниже касательной, а с другой – выше.
Теорема 3.2. Если в точке  вторая производная функции
вторая производная функции
y = f(x) равна нулю или не существует, а при переходе через точку  знак второй производной меняется на противоположный, то данная точка является точкой перегиба.
знак второй производной меняется на противоположный, то данная точка является точкой перегиба.
Доказательство данной теоремы следует из того, что знаки 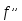 (x) по разные стороны от точки
(x) по разные стороны от точки  различны. Значит, с одной стороны от точки функция выпукла, а с другой – вогнута. В этом случае, согласно определению 3.2, точка
различны. Значит, с одной стороны от точки функция выпукла, а с другой – вогнута. В этом случае, согласно определению 3.2, точка  является точкой перегиба.
является точкой перегиба.
Исследование функции на выпуклость и вогнутость проводится по той же схеме, что и исследование на экстремум.
|
|
|
Асимптоты функции
В предыдущих пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны.
Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на бесконечность и когда при разрыве второго рода в конечной точке уходит на бесконечность сама функция. В обоих этих случаях может возникнуть ситуация, когда функция будет стремиться к некоторой прямой, называемой ее асимптотой.
Определение. Асимптотой графика функции y = f(x) называется прямая линия, обладающая тем свойством, что расстояние от графика до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Различают два типа асимптот: вертикальные и наклонные.
К вертикальным асимптотам относятся прямые линии x =  , которые обладают тем свойством, что график функции в их окрестности уходит на бесконечность, то есть, выполняется условие:
, которые обладают тем свойством, что график функции в их окрестности уходит на бесконечность, то есть, выполняется условие:  .
.
Очевидно, что здесь удовлетворяется требование указанного определения: расстояние от графика кривой до прямой x =  стремится к нулю, а сама кривая при этом уходит на бесконечность. Итак, в точках разрыва второго рода функции имеют вертикальные асимптоты, например, y =
стремится к нулю, а сама кривая при этом уходит на бесконечность. Итак, в точках разрыва второго рода функции имеют вертикальные асимптоты, например, y =  в точке x = 0. Следовательно, определение вертикальных асимптот функции совпадает с нахождением точек разрыва второго рода.
в точке x = 0. Следовательно, определение вертикальных асимптот функции совпадает с нахождением точек разрыва второго рода.
Наклонные асимптоты описываются общим уравнением прямой линии на плоскости, то есть y = kx+b. Значит, в отличие от вертикальных асимптот, здесь необходимо определить числа k и b.
Итак, пусть кривая  = f(x) имеет наклонную асимптоту, то есть при x
= f(x) имеет наклонную асимптоту, то есть при x 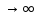 точки кривой сколь угодно близко подходят к прямой
точки кривой сколь угодно близко подходят к прямой  = kx+b (рис. 4.1). Пусть M(x,y) - точка, расположенная на кривой. Ее расстояние от асимптоты будет характеризоваться длиной перпендикуляра |MN|.
= kx+b (рис. 4.1). Пусть M(x,y) - точка, расположенная на кривой. Ее расстояние от асимптоты будет характеризоваться длиной перпендикуляра |MN|.
Согласно определению,
 .
.
Но |MN| вычисляется довольно сложно, гораздо проще найти |MN|=|  |.
|.
Из треугольника MNP следует, что
|MN|=|MP|cos  ,
,
так как  PMN =
PMN =  .
.
Значит,
 .
.
Итак,
 0.
0.
Но выше было сказано, что
 =|
=|  |=| f(
|=| f(  ) - (kx+b) |,
) - (kx+b) |,
откуда следует, что
 0.
0.
Вынесем x в данном выражении за скобки:
 (x |
(x |  – k –
– k –  |)=0.
|)=0.
Так как по условию 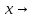 0, то
0, то  |
|  – k –
– k –  | =0.
| =0.
Здесь 
 0, следовательно,
0, следовательно,  |
|  – k | =0, откуда получаем:
– k | =0, откуда получаем:
k =  .
.

Рис. 4.1
Зная k, рассмотрим снова предел:  |(f(x) – kx)-b | =0. Он выполняется лишь при условии, что b =
|(f(x) – kx)-b | =0. Он выполняется лишь при условии, что b =  [ f(x) – kx ].
[ f(x) – kx ].
Таким образом, найдены k и b, а с ними и уравнение наклонной асимптоты. Если k = 0, то получаем частный случай горизонтальной асимптоты
|
|
|
y = b. При невозможности найти хотя бы один предел (при вычислении k или b) делается вывод, что наклонной асимптоты нет.
Аналогично проводится исследование и при x  .
.
|
|
|


