Предварительно затянутый болт дополнительно нагружен внешней осевой растягивающей силой; последующая затяжка болта отсутствует или возможна.

Этот вид нагружения самый распространенный, так как для большинства резьбовых соединений требуется предварительная затяжка болтов, обеспечивающая плотность соединения и отсутствие взаимных смещений деталей стыка, нарушающих работу соединения. К болтам этой категории относятся фланцевые, фундаментные и т. п.

После предварительной затяжки болта силой F₃ болт растягивается, а детали стыка сжимаются. При действии на болтовое соединение внешней сипы F (рис. 3) только часть ее χ F дополнительно нагружает болт, а остальная часть (1— χ )F идет на частичную разгрузку деталей стыка от сжатия (рис. 4). Коэффициент χ учитывающий долю внешней нагрузки F, приходящуюся на болт, называется коэффициентом внешней (основной) нагрузки.

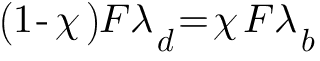Так как задача о распределении силы F между болтом и стыком статически неопределима, то она решается с помощью условия совместности деформаций. При действии на соединение внешней силы F до раскрытия стыка сжатие соединяемых болтом деталей уменьшается на столько, на сколько болт растягивается, т. е.

где λ_d — коэффициент податливости соединяемых болтом деталей;
λ_b — коэффициент податливости болта, т. е. удлинение болта при растя жении под действием силы в 1 Н. Из уравнения следует, что коэффициент внешней нагрузки

 

 

Коэффициент податливости болта

где l — длина деформируемой части стержня болта, принимаемая равной толщине сжимаемых болтом соединяемых деталей;
А — площадь поперечного сечения стержня болта (для ступенчатого стержня — средняя приведенная площадь сечения);
Е - модуль упругости материала болта.

 

45 Болт, установленный в отверстие с зазором (рис. 8), нагружен поперечной силой.

Рис. 8

В этом случае болт затягивается такой силой затяжки F₃, чтобы возникающая при этом сила трения F_ƒ на поверхности стыка соединяемых деталей была не меньше внешней сдвигающей поперечной силы F. В результате этого болт работает на растяжение от силы F₃. Необходимую силу затяжки болта определяют из условия

откуда

где ƒ - коэффициент трения между соединяемыми деталями; для чугунных и стальных деталей ƒ=0,15...0,2.

Проектный расчет болта в этом случае производят с учетом 20%-ного запаса от сдвига деталей и с учетом крутящего момента при затяжке болта см. формулу

по формуле
или

 

Для уменьшения диаметра болта, установленного в отверстии с зазором и нагруженного поперечной силой, применяют различные устройства, разгружающие болт от восприятия поперечных сил, например разгрузочную втулку (рис. 9), шпонку (рис. 10), штифт и т. д. При использовании разгрузочного устройства диаметр болта обычно принимают конструктивно.

 

 

Шлицевые (зубчатые) соединения способны передавать большие вращающие моменты и обеспечивают хорошее центрирование детали на валу. Они могут быть подвижными и неподвижными. По мере профиля шлицев различают соединения:

• прямоточные по ГОСТ 1139-80;
• эвольвентные с углом профиля 30° по ГОСТ 6033-80;
• треугольные с углом профиля 60, 72 и 90°.

Допуски и посадки для соединений с прямобочным профилем установлены ГОСТ 1139-80. Их условное обозначение содержит букву, обозначающую поверхность центрирования (D, d или b), число зубьев z, номинальные значения основных размеров D, d и b, обозначения посадок диаметров размера b, помещенные после соответствующего размера. Допуски нецентрирующего диаметра можно не указывать. Например: D-8x42x48(H8/h7)x8(F10/h9).

Легкая серия	Средняя серия	Тяжелая серия
Номинальный размер "z" x "d" x "D"	b	Номинальный размер "z" x "d" x "D"	b	Номинальный размер "z" x "d" x "D"	b
6x23x26		6x11x14		10x16x20	2,5
6x26x30		6x13x16	3,5	10x18x23
6x28x32		6x16x20		10x21x26
8x32x36		6x18x22		10x23x29
8x36x40		6x21x25		10x26x32
8x42x46		6x23x28		10x28x35
8x46x50		6x26x32		10x32x40
8x52x58		6x28x34		10x36x45
8x56x62		8x32x38		10x42x52
8x62x68		8x36x42		10x46x56
10x72x78		8x42x48		16x52x60
10x82x88		8x46x54		16x56x65
10x92x98		8x52x60		16x62x72
10x102x108		8x56x65		16x72x82
10x112x120		8x62x72		20x82x92
		10x72x82		20x92x102
		10x82x92		20x102x115
		10x92x102		20x112x125
		10x102x112
		10x112x125
"z" - число шлицев, "d" - внутренний диаметр, "D" - наружный диаметр, "b" - ширина шлица

 

 

47

 

Расчет угловых швов

В обычных угловых швах (фланговых, лобовых), выполненных ручной сваркой, расчетная высота рабочего сечения d _ш (рис. 75, а) принимается по биссектрисе угла сечения валика равной (без учета наплыва) d_ш, = 0,7 h_ш, где h_ш— толщина шва (по катету); в пологих швах — d_ш принимается по меньшему катету. В вогнутых швах за d_ш принимается фактическая толщина шва по биссектрисе (рис. 75, б). При глубоком проплавлении автоматической или полуавтоматической сваркой (или специальными электродами с тугоплавкими обмазками— ультракороткой дугой) принимаются большие величины рабочей толщины шва — вплоть до d_ш = h_ш (рис. 75, в).
Распределение напряжений по длине швов (лобовых, фланговых) или при обварке по контуру принимается равномерным.

Таким образом, напряжение в угловом шве определяется по формуле

Здесь d_ш = bh_ш, где коэффициент b принимается равным: при ручной сварке b = 0.7; при полуавтоматической сварке b =0,8; при автоматической сварке и ультракороткой дуге (при однопро­ходной сварке) b =1.
При прикреплении несимметричных профилей, например уголка (рис. 76), длины или площади швов должны быть так распределены, чтобы прикрепляемый элемент не получал дополнительного изгиба от эксцентриситета (площади швов должны быть распределены обратно пропорционально расстояниям от шва до оси элемента).

Таким образом, при требуемой площади швов

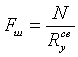
площадь большего шва равна

площадь меньшего шва равна

Наименьшая толщина угловых швов принимается в зависимости от толщины прикрепляемых элементов и составляет:

При толщине элементов	4—9	10 - 14	15-25	26-40	>45 мм
Толщина шва					12 мм

Толщины угловых швов должны быть по возможности унифицированы. Наиболее рационально иметь в конструкции не более двух размеров толщины (чаще всего 6 — 8 мм). Для того чтобы избежать чрезмерно длинных прикреплений, длине каждого флангового шва, передающего продольную осевую силу, огра­ичивается величиной 60 h_ш; наименьшая расчетная длина флангового или лобового шва принимается равной 40 мм или 4 h_ш в связи с резкой концентрацией напряжений в коротких швах (рис. 77, б).

При малых усилиях могут применяться прерывистые угловые швы. Они нерациональны как по характеру их работы, так и по производственным условиям, но дают экономию наплавленного металла. Усилие передается на участки прерывистого шва поровну, Расстояние между участками прерывистого шва в сжатых элементах по условиям устойчивости сплачиваемых элементов должно составлять не более 15 d (где d — толщина самого тонкого элемента), в растянутых — не более 30 d (рис. 77, в).

При простой нахлестке элементов, соединяемых двумя лобовыми швами, расстояние между швами с точки зрения уменьшения сварочных напряжений должно быть не менее 5 d (рис. 77, г).

 

49 Болт, установленный в отверстие из-под развертки без зазора (рис. 11), нагружен поперечной силой.

В этом случае болт рассчитывают на срез; условие прочности болта

где τ_с — расчетное напряжение среза болта;
F — поперечная внешняя сила, срезающая болт;
d₀ — диаметр стержня болта в опасном сечении;
[τ_с] — допускаемое напряжение на срез болта.

Предыдущей Формулой пользуются при проверочном расчете болта. Проектный расчет выполняют по формуле

Если болтом соединяют тонкие детали, то необходимо производить проверку прочности деталей их смятие по формуле

где h — длина наиболее сминаемой части стержня болта;
σ_sm — расчетное напряжение смятия в болтовом соединении;
[σ_sm] — допускаемое напряжение на смятие болтового соединения.

 

 

Упорная резьба применяется в тех случаях, когда имеются большие односторонние нагрузки, действующие в осевом направлении. Профиль упорной резьбы представляет собой трапецию, одна сторона которой имеет угол наклона 3° и является рабочей стороной профиля, а другая сторона 30°, которая не используется в качестве рабочей.

Обозначается упорная резьба буквой S:

S40 × 7 – номинальный диаметр 40мм с шагом 7 мм.

S32 × 6 – номинальный диаметр 32мм с шагом 6 мм.

S52 × 8 LH – диаметр 52мм с шагом 8 мм, резьба левая.

S36 × 12 (P6) – диаметр 36мм, резьба многозаходная, с шагом 6мм, значение хода 12мм.

 

Соединения шлицевые треугольные не стандартизованы и применяются как неподвижные при тонкостенных ступицах, пустотелых валах, стесненных габаритах деталей и сравнительно небольших вращающих моментах. Центрирование соединения выполняется по боковым поверхностям зубьев. Треугольные шлицевые соединения бывают цилиндрическими и коническими.  
Треугольное шлицевое соединение имеет более ограниченное применение, чем прямобочное и эвольвентное. По малой  
Наиболее важными преимуществами шлицевых соединений перед шпоночными является возможность передачи больших крутящих моментов, высокая прочность и надежность соединения, повышенная точность центрирования и направления втулок на валу.Шлицевые соединения в зависимости от профиля зубьев разделяются на прямобочные, эвольвентные и треугольные. Шлицевые соединения с эвольвентным профилем зубьевимеют существенные преимущества по сравнению с прямобочными они могут передавать большие крутящие моменты, имеют на 10 — 40% меньше концентрацию напряжений у основания зубьев, повышенную циклическую прочность, обеспечивают лучшее центрирование и направление деталей, проще н изготовлении. Шлицевые соединения с треугольным профилем не стандартизованы их применяют чаще всего вместо посадок с натягом, а также при тонкостенных втулках для передачи небольших крутящих моментов.
Треугольные шлицевые соединения (рис. 22) применяют преимущественно для неподвижных конструкций и передачи малых крутящих моментов. Центрирование втулки производится только по боковым сторонам зубьев.

Условие прочности одностороннего лобового шва на срез:

где — расчетное и допускаемое напряжения среза для шва (см. табл.5); l _ш — длина шва; F — нагрузка, действующая на шов.

Проектировочный расчет. Длину одностороннего лобового углового шва (см. рис. 19) при осевом нагружении определяют по формуле

длина двустороннего лобового углового шва

 

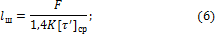
К динамическим нагрузкам, несмотря на отсутствие зна- чительных инерционных сил, можно отнести периодиче- ские многократно повторяющиеся (циклические) нагруз- ки, действующие на элементы конструкции. Такого рода нагружения характерны для большинства машинострои- тельных конструкций, таких, как оси, валы, штоки, пру- жины, шатуны и т. д. Как показывает практика, нагрузки, циклически изме- няющиеся во времени по величине или по величине и по знаку, могут привести к разрушению конструкции при напряжениях, существенно мень- ших, чем предел текучести (или предел прочности). Такое разрушение принято называть «уст а л о с т н ы м». Материал как бы «устает» под действием многократных перио- дических нагрузок. Усталостное разрушение – разрушение материала под действием повторно- переменных напряжений. Усталость материала – постепенное накопление повреждений в материале под действием переменных напряжений, приводящих к образованию трещин в материале и разрушению. Выносливость – способность материала сопротивляться усталостному раз- рушению. Физические причины усталостного разрушения материалов достаточно сложны и еще не до конца изучены. Одной из основных причин усталостного разрушения принято считать образование и развитие трещин. Механизм усталостного разрушения во многом связан с неоднородностью реальной структуры материалов (разли- чие размеров, очертаний, ориентации соседних зерен ме- талла; наличие различных включений – шлаков, приме- сей; дефекты кристаллической решетки, дефекты поверх- ности материала – царапины, коррозия и т. д.). В связи с указанной неоднородностью при переменных напряжени- ях на границах отдельных включений и вблизи микроско- пических пустот и различных дефектов возникает концен- трация напряжений, которая приводит: к микропластическим деформациям сдвига некоторых зе- рен металла (при этом на поверхности зерен могут появ- ляться полосы скольжения) и накоплению сдвигов (кото- 57 рое на некоторых материалах проявляется в виде микроскопических бугор- ков и впадинок – экструзий и интрузий); затем происходит развитие сдвигов в микротре- щины, их рост и слияние; на последнем этапе появляется одна или несколь- ко макротрещин, которая достаточно интенсивно развивается (растет). Края трещины под действием переменной нагрузки притираются друг об друга, и поэтому зона роста трещины отличается гладкой (полированной) поверхностью. По мере роста трещины поперечное сечение детали все больше ослабляется, и наконец происходит вне- запное хрупкое разрушение детали, при этом з о - н а хрупкого дол о м а имеет грубозернистую кристаллическую структуру (как при хрупком раз- рушении).

асимметричный цикл – максимальное и мини- мальное напряжения не равны по абсолютной ве- личине (σmax ≠ −σmin in −σmin), при этом асимметричный цикл может быть знак опеременным или знакопостоянным;

Цилиндрические зубчатые колеса бывают прямозубые, косозубые, с шевронными и винтовыми зубьями
Прямозубые,косозубыеишевронные(рис. 57, а, б, в, д) применяют для передач между параллельными валами, с которыми зубчатые колеса связываются шпоночными соединениями. Колеса с винтовыми зубьями применяют для передач со скрещивающимися валами (рис. 57,г).
Конические зубчатые колеса(рис. 57, е) применяют для передач с пересекающимися осями.
Передача движения зубчатыми колесами производится зубьями двух сопряженных, т. е. сцепляющихся между собой и взаимодействующих, зубчатых колес. Зубья одного колеса входят во впадины другого и при вращении одного колеса вращается другое.
Зубчатое колесо, передающее вращение от ведущего вала, называется ведущим, а второе — ведомым.
Различают следующие элементы зубчатого колеса (рис. 58):

диаметр выступов зубчатого колеса D_e;

диаметр делительной (начальной) окружности зубчатого колеса d,

диаметр основной окружности зубчатого колеса d₀,

диаметр впадин зубчатого колеса D_i,

высота головки зуба зубчатого колеса h',

высота ножки зуба зубчатого колеса h",

высота зуба зубчатого колеса h = h' + h",

шаг зацепления зубчатого колеса t,

толщина зуба зубчатого колеса S,

ширина впадины зубчатого колеса S₁,

межцентровое расстояние, длина зуба, модуль m и число зубьев z зубчатого колеса.

Исходными данным, характеризующими зубчатое колесо, являются модуль и число зубьев, остальные величины определяются от исходных.

Модуль зубчатого колеса m (измеряется в мм) представляет собой длину, приходящуюся по диаметру делительной окружности на один зуб колеса. Численно модуль равен m = d/z = t/π мм. (28)

Произведение модуля m на π дает величину t — расстояние между двумя одноименными точками смежных зубьев по делительной окружности.

Остальные элементы зубчатого колеса определяются по формулам (размеры в мм):

диаметр делительной окружности зубчатого колеса d = mz; (29)

диаметр окружности выступов зубчатого колеса D_e = m(z + 2);(30)

диаметр окружности впадин зубчатого колеса D_i = m(z -2,25) (31)

толщина зуба зубчатого колеса S = (9/20) • t;(32)

ширина впадины зубчатого колеса S₁= (11/20) * t; (33)

высота зуба зубчатого колеса h = h' + h" = 2,25*m; (34)

высота головки зуба зубчатого колеса h' = m; (35)

высота ножки зуба зубчатого колеса h"= 1,25m; (36)

длина зуба зубчатого колеса b = 10m; (37)

расстояние между центрами двух зубчатых колес, находящихся в зацеплении, L= m*((z₁+z₂)/2). (38)

Зубчатая передача имеет постоянное передаточное отношение, позволяющее определить по известным величинам числа оборотов ведущего, а также ведомого колеса.

Передаточным отношением называется отношение числа зубьев ведущего колеса к числу зубьев ведомого, обозначается оно буквой i в отличие от передаточного числа, обозначаемого 1/i. Передаточное отношение и передаточное число находятся соответственно из уравнений:

i= z₁/z₂ = n₂/n₁; (39)

1/i = n₁/n₂ = z₂/z₁.(40)

Кинематические цепи, состоящие: а — из пары зубчатых колес, б — из цилиндрических, конической и червячной пар

Если взять число оборотов в минуту n ведущего вала и умножить на передаточное отношение одной пары зубчатых колес i = z₁ / z₂ (рис. 59, а), то из уравнения n₂= n₁ * (z₁/z₂) можно найти число оборотов в минуту n₂ведомого вала. При расчете числа оборотов конечного звена кинематической цепи (рис. 59,б.) находить передаточное отношение каждой пары нет смысла, можно взять сразу передаточное отношение всей цепи и умножить его на число оборотов в минуту n₁ ведущего вала.

Таким образом, число оборотов конечного звена n₅ = n₁ *(z₁z₃kz₆ / z₂z₄z₅z₇), (41)

где k — число заходов червяка.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: