 |
Что такое теория игр? Специфика задач теории игр.
|
|
|
|
Финансово-экономические операции в условиях рыночных отношений часто характеризуются наличием противоположных интересов различных оперирующих сторон, которые пытаются достичь своих целей часто в ущерб друг другу.
В этой связи при разработке управленческого решения в условиях конфликта особое место занимает выбор и сравнительный анализ возможных (допустимых) способов (стратегий) действий.
Раздел теории исследования операций, связанный с математическим моделированием конфликта и поиском оптимальных решений в его условиях, называют теорией игр. Задачи теории игр относятся к области принятия решений в условиях неопределенности, а их специфика состоит в том, что, как правило, подразумевается неопределенность, возникающая в результате действий двух или более “разумных” противников, способных оптимизировать свое поведение за счет других. Среди типичных примеров такого поведения могут быть названы действия конкурирующих фирм на одном рынке или планирование военных операций. Причины или источники неопределенности результата (исхода) относятся к трем группам:
· комбинаторные источники (шахматы);
· влияние случайных факторов (игра в орлянку, кости, карточные игры, где расклад является случайным);
· стратегическое происхождение неопределенности: игрок не знает, какого образа действий придерживается его противник; здесь неопределенность исходит от другого лица; соответствующие игры называются стратегическими.
Таким образом, в стратегической игре действия предпринимают две или более стороны, в отличие от нестратегической игры, в которой действия предпринимает одна сторона, а остальные являются заинтересованными сторонами.
|
|
|
Одним из основных вопросов в задачах с коллективным выбором решений является вопрос об определении оптимальности, т.е. вопрос, какие решения следует признавать наилучшими в ситуации оптимизации по нескольким критериям, отражающим различные интересы. Многие методы решения проблем теории игр основываются на сведении их к задачам математического программирования.
- Понятие игры. Классификация игр.
Теория игр берет начало от работ Э. Бореля (1921г.), а принципиальным этапом в её становлении как самостоятельного научного направления стала монография Дж. Неймана, опубликованная в 1944г.
Игра – это упрощенная математическая модель реальной ситуации, которая предполагает наличие следующих компонент:
a) заинтересованных сторон;
b) возможных действий каждой стороны;
c) интересов сторон.
Интересы участников могут быть как антагонистические (полностью противоположные) так и неантагонистические. В последнем случае может исследоваться вопрос о наиболее эффективных совместных действиях (кооперативные игры). Предполагается, что известны варианты действий сторон (стратегии), исход игры для каждого участника в случае выбора конкретных действий всеми участниками, степень и порядок информированности каждого участника игры о поведении всех других участников.
Конфликт может возникнуть не только в результате действий различных участников, но и в результате действий тех или иных “стихийных сил”. В этом случае их называют “игры с природой”.
Классифицируются игры по разным признакам:
· по числу игроков (игры с двумя, тремя и более противников);
· по числу стратегий (конечные и бесконечные игры);
· по свойствам функции выигрыша (с нулевой суммой; с постоянной разностью);
· по возможности предварительных переговоров между участниками (кооперативные и некооперативные).
Кроме этого выделяются различные классы игр по иным признакам (дифференциальные, статистические и многие другие).
|
|
|
Игра ведется по определенным правилам. Каждый участник принимает такие решения, которые, как он полагает, могут обеспечить ему наилучший результат (исход).
Исход игры – это значение некоторой функции, называемой функцией выигрыша (платежной функцией). Если сумма выигрышей игроков равна нулю, то игру называют игрой с нулевой суммой. Если в игре принимают два участника, то её называют парной.
- Парные матричные игры с нулевой суммой.
Элементы матрицы могут быть положительными, отрицательными или равными нулю. Случай, когда элемент матрицы положителен, означает, что игрок В в определенной ситуации должен уплатить игроку А сумму, равную значению этого элемента. Если элемент отрицателен, игрок А уплачивает игроку В сумму, равную абсолютному значению этого элемента. И, наконец, если этот элемент равен нулю, выплаты не производятся. Таким образом в игре двух лиц с нулевой суммой один игрок выигрывает столько же, сколько проигрывает другой (все выплаты производятся из “карманов” противников) Это и объясняет название – игра с нулевой суммой. Игрок А стремится к максимальному выигрышу, игрок В - к минимальному проигрышу. Решить игру – значить найти оптимальные стратегии игроков и их выигрыши.
Данная форма представления конечных игр двух лиц объясняет общее для них название – матричные игры.
- Чистые стратегии, платежная матрица, верхняя и нижняя цена игры.
Чистая стратегия – конечное число возможных действий игрока.
Игрок А может выбрать любую стратегию 
в ответ игрок В может выбрать любую свою чистую стратегию 
Выбор пары стратегий 
однозначно определяет результат 
выигрыш игрока А. При этом проигрыш игрока В составляет 
. Если известны значения - выигрыши для каждой пары чистых стратегий, то можно составить матрицу выигрышей игрока А (проигрышей игрока В). Эту матрицу называют платежной.
Стратегия 1 игрока 2 ( )
| Стратегия 2 игрока 2 ( )
| ……………. | Стратегия n игрока 2 ( )
| |
Стратегия 1 игрока 1 ( )
| 
| 
| ……………. | 
|
Стратегия 2 игрока 1 ( )
| 
| 
| ……………. | 
|
| ………….. | ………….. | ……………. | ……………. | ……………… |
Стратегия m игрока 1 ( )
| 
| 
| ……………. | 
|
Введем в рассмотрение числа
|
|
|
- минимально возможный выигрыш игрока А, если он применит стратегию 
и 
- максимально возможный проигрыш игрока В, если он применит стратегию 
.
Тогда платежная матрица будет иметь следующий вид:
| Игрок 2 Игрок 1 | Стратегия 1 ()
| Стратегия 2 ()
| ………… | Стратегия n()
| Минимум по строкам |
| Стратегия 1 ()
|
|
| …………. |
| 
|
| Стратегия 2 ()
|
|
| …………. |
| 
|
| ………….. | …………… | …………. | …………. | …………… | ………….. |
| Стратегия m()
|
|
| …………. |
| 
|
| Максимум по столбцам | 
| 
| …………. | 
|
Игрок А выберет такую стратегию, которая гарантирует ему наибольший из наименьших выигрышей при любой стратегии противника (максиминный выигрыш). Этот выигрыш определяется формулой 
.Величина 
называется нижней чистой ценой игры, а соответствующая ему чистая стратегия - максиминная стратегия.
игрок В, действуя рационально, выберет такую стратегию, которая гарантирует ему наименьший из возможных проигрышей при любых действиях противника. Принято говорить, игрок В руководствуется принципом минимаксного проигрыша. Этот проигрыш определяется выражением 
. Величину 
называют верхней чистой ценой игры, а соответствующую ему чистую стратегию – минимаксной стратегией. Принцип осторожности, который определяет выбор партнерами стратегий, соответствующий максиминному выигрышу или минимаксному пригрышу, часто называют принципом минимакса.
Для любой игры с нулевой суммой 
чем и объясняются названия “нижняя цена” и “верхняя цена”.
- Седловая точка. Решение игры в чистых стратегиях.
Если 
, то говорят, что игра имеет седловую точку в чистых стратегиях и чистую цену игры 
. Пару чистых стратегий , соответствующих и , называют седловой точкой матричной игры; - седловым элементом платежной матрицы. Стратегии и , образующие седловую точку, являются оптимальными. Тройка 
называется решением игры.
- Смешанные стратегии. Цена игры.
Игра двух лиц с нулевой суммой далеко не всегда имеет седловую точку. Для игр без седловой точки оптимальные стратегии игроков находятся в области смешанных стратегий.
|
|
|
Рассмотрим антагонистическую парную игру с нулевой суммой. Пусть игра не имеет седловой точки.
Смешанной стратегией игрока А называется вектор 
координаты которого удовлетворяют условиям: 
вероятности, с которыми игрок А выбирает свои чистые стратегии .
Смешанной стратегией игрока В называется вектор 
координаты которого удовлетворяют условиям: 
вероятности, с которыми игрок В выбирает свои чистые стратегии .
При использовании смешанных стратегий игра приобретает случайный характер, случайной становится и величина выигрыша игрока А (проигрыша игрока В).
Эта величина является функцией смешанных стратегий и определяется по формуле: 
.
Функцию 
называют функцией выигрыша или платёжной функцией.
Смешанные стратегии 
называют оптимальными, если они образуют седловую точку для платёжной функции , т.е. 
Величину 
называют ценой игры.
- Решение матричной игры сведением к задаче линейного программирования.
Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и, наоборот, каждая задача линейного программирования может быть представлена как игра.
Из основного положения теории стратегических игр следует, что при использовании смешанных стратегий существует, по меньшей мере, одно оптимальное решение с ценой игры 
, причем 
, т.е. цена игры находится между верхним и нижним значением игры. Величина неизвестна, но всегда можно предположить, что 
. Это условие выполняется, поскольку всегда можно путем соответствующего преобразования матрицы сделать все её элементы положительными. Таким образом, если в исходной платежной матрице имеется хотя бы один неположительный элемент, то первым шагом в процедуре сведения игры к задаче линейного программирования должно быть ее преобразование к матрице, все элементы которой строго положительны. Для этого достаточно увеличить все элементы исходной матрицы на одно и то же число 
. При таком преобразовании матрицы оптимальные стратегии игроков не изменяются.
Допустим, что смешанная стратегия игрока А складывается из стратегий 
с вероятностями, соответственно 
. Оптимальная смешанная стратегия игрока В складывается из стратегий 
с вероятностями 
Условия игры определяются платежной матрицей:
|
|
| … |
| 
| |
|
|
|
| … |
|
|
|
|
|
| … |
|
|
| … | … | … | … | … | … |
|
|
|
| … |
|
|
| 
|
| … |
|
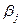
Если игрок А применяет оптимальную смешанную стратегию, а игрок В – чистую стратегию , то средний выигрыш игрока А (математическое ожидание выигрыша) составит 
.
|
|
|
Игрок А стремится к тому, чтобы при любой стратегии игрока В его выигрыш был не менее, чем цена игры , и сама цена игра была максимальной. Такое поведение игрока А описывается следующей моделью линейного программирования:
или, обозначив, 
, задачу можно переписать в следующем виде:
В результате решения поставленной задачи, находим оптимальный вектор 
и 
, а затем, находим цену игры 
и координаты вектора 
.
Поведению игрока В соответствует двойственная задача:
Решив эту задачу, получим оптимальный вектор 
и 
, а затем – цену игры 
и координаты вектора 
Таким образом, оптимальные смешанные стратегии игроков А и В 
и 
могут быть найдены в результате решения пары двойственных задач линейного программирования.
Если исходная матрица увеличивалась на d, то для получения цены первоначальной игры значение v нужно уменьшить на d.
Если смешанная стратегия 
такова, что одно из значений 
, а следовательно все остальные равны нулю, то такая стратегия называется чистой стратегией игрока. Чистая стратегия уже не является случайной.
- Игры с природой. Специфика игр с природой.
Игры с природой образуют специальный класс матричных игр, в которых одним из участников является человек или группа лиц, объединенных общностью цели (игрок А), а другим – «природа» (игрок П). Под термином «природа» подразумевается весь комплекс внешних условий, при которых игроку А приходится принимать решение. Природа безразлична к выигрышу и не стремится обратить в свою пользу промахи игрока А.
Игрок А может использовать т стратегий А1,А2,…,А т, а природа может реализовать п различных состояний П1,П2,…,П п. Игроку А могут быть известны вероятности qj, с которыми природа реализует свои состояния Пj. Действуя против природы, игрок А может пользоваться как чистыми А i, так и смешанными 
стратегиями. Если он имеет возможность численно оценить (величиной аij) последствия применения каждой своей чистой стратегии А i при любом состоянии П j природы, то игру можно задать платежной матрицей.
| 
| … | 
| 
| |
|
|
|
| … |
| 
|
|
|
|
| … |
| 
|
| … | … | … | … | … | … |
|
|
|
| … |
| 
|
|
|
|
| … |
|
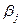
При упрощении платежной матрицы игры с природой имеется своя специфика: отбрасывать те или иные состояния природы нельзя, так как она может реализовать любое состояние не зависимо от того, выгодно оно или нет.
При выборе оптимальной стратегии игрока А пользуются различными критериями. При этом опираются как на платежную матрицу, так и на матрицу рисков.
Риском rij игрока А, когда он пользуется чистой стратегией А i при состоянии П j природы, называется разность между максимальным выигрышем 
, который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние П j, и тем выигрышем, который он получит, используя стратегию А i, не зная какое же состояние природа реализует. Таким образом, элементы матрицы рисков определяются по формуле 
где 
- максимально возможный выигрыш игрока А при состоянии П j
|
|
| … |
| 
| |
|
|
|
| … |
| 
|
|
|
|
| … |
|
|
| … | … | … | … | … | … |
|
|
|
| … |
| 
|
| 
| 
| … | 
|
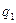
- Критерий Байеса
Если вероятности qj состояний природы известны, то пользуются критериями Байеса и Лапласа.
В качестве оптимальной по критерию Байеса принимается чистая стратегия А i, при которой максимизируется средний выигрыш 
игрока А.
- Критерий Лапласа.
Если игроку А представляются в равной мере правдоподобными все состояния природы, то 
и оптимальной по критерию Лапласа считается чистая стратегия А i, обеспечивающая 
.
- Критерий Вальда.
Оптимальной по критерию Вальда считается чистая стратегия А i, при которой наименьший выигрыш 
игрока А будет максимальным.
- Критерий Сэвиджа.
Оптимальной по критерию Сэвиджа считается та чистая стратегия А i, при которой минимизируется величина максимального риска, т.е. обеспечивается 
.
- Критерий Гурвица.
Оптимальной по критерию Гурвица считается чистая стратегия А i, найденная из условия 
где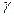 
принадлежит интервалу (0,1) и выбирается из субъективных соображений.
|
|
|
