Модель CA РM и ее обобщение

В самом начале 60-х годов учеником Марковица У. Шарпом была предложена так называемая однофакторнаямодельрынка капиталов, в которой впервые появились ставшие знаменитыми впоследствии "альфа" и "бета"- характеристики акций. На основе однофакторной модели Шарп впоследствии предложил упрощенный метод выбора оптимального портфеля, который сводил задачу квадратичной оптимизации к линейной. В простейших случаях, для небольших размерностей, эта задача могла быть решена практически "вручную". Такое упрощение сделало методы портфельной оптимизации применимыми на практике. К 70-м гг. развитие программирования, а также совершенствование статистической техники оценивания показателей "альфа" и "бета" отдельных ценных бумаг и индекса доходности рынка в целом привело к появлению первых пакетов программ для решения задач управления портфелем ценных бумаг.

Первоначально Шарпом преследовалась цель упростить получение исходных данных (прежде всего, ковариаций между доходностями ценных бумаг), необходимых для решения задачи оптимизации портфеля по Марковицу. Для этого была использована однофакторная модель зависимости доходности долгосрочной рисковой ценной бумаги от фактора - средневзвешенной по капитализации фондовых активов доходности рынка:

 ,                                                      (2.11)

где  - общее число всех обращающихся на рынке ценных бумаг,

   - соответственно доля в общей капитализации рынка и доходность -ой ценной бумаги.

Однофакторная модель доходности -ой ценной бумаги строится как линейная регрессионная зависимость, получаемая по методу наименьших квадратов:

,                  (2.12)

где 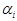 - коэффициент смещения регрессионной модели, отражающий активную доходность - дополнительную доходность данной ценной бумаги относительно  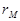- и степень интереса инвесторов к ней,

 - коэффициент чувствительности изменения доходности ценной бумаги относительно изменения доходности среднерыночного портфеля,

- погрешность регрессионной модели, отражающая влияние всех других факторов.

Регрессионная зависимость строится в предположении о зависимости доходностей всех ценных бумаг только от одного фактора - 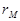 и, следовательно, взаимной некоррелированности ошибок , а из алгоритма метода наименьших квадратов следует, что

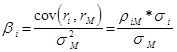,              (2.13)

где  - СКО соответственно доходностей -ой ценной бумаги и среднерыночного портфеля,

 - коэффициент корреляции между доходностью -ой ценной бумаги и доходностью среднерыночного портфеля.

Если известны коэффициенты  для всех рисковых фондовых активов (а к выводу о необходимости их оценки ввиду наглядности практика фондового рынка пришла довольно быстро), то ковариации доходностей ценных бумаг и их дисперсии могут быть вычислены применением правил теории вероятностей к (2.12):

                                                     ,          (2.14)

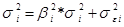
Эти правила легко обобщаются на случай портфеля, состоящего из  рисковых ценных бумаг, представленных в нем долями  :

 

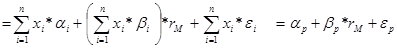, (2.15)

где   ,                                                                (2.16)

      ,                                                              (2.17)

                                                                            (2.19)                                         

Риск портфеля определяется:

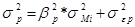         ,                                               (2.20)

где       .                                                    (2.21)

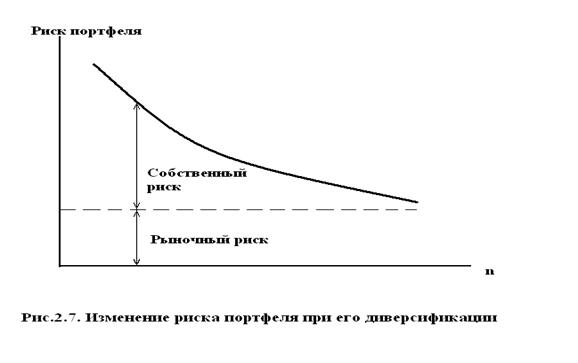
Первое слагаемое в (2.20) характеризует рыночный (систематический, недиверсифицируемый) риск, а второе - собственный риск портфеля, который может быть уменьшен за счет диверсификации как показано на рис.2.7.

Однако по-настоящему значимое научное и практическое значение регрессионная аппроксимация в виде (2.12) и (2.13) получила в связи с использованием результатов Тобина для моделирования ценообразования долгосрочных активов на фондовом рынке.

С 1964 г. появляются работы Шарпа, Линтнера, Моссина, открывшие следующий этап в инвестиционной теории, связанный с так называемой моделью оценки капитальных активов, или САРМ (Capital Asset Pricing Model). Результаты, полученные в этих работах, основаны на исходных предположениях Марковица (см. п.2.2), дополненных следующими:

1. Для всех инвесторов период вложения одинаков.

2. Информация свободно и незамедлительно доступна для всех инвесторов.

3. Инвесторы имеют однородные ожидания, т.е. одинаково оценивают будущие доходности, риск и ковариации доходностей ценных бумаг.

4. Безрисковая процентная ставка одинакова для всех инвесторов

В совокупности все исходные предположения описывают так называемый совершенный рынок ценных бумаг, на котором отсутствуют препятствующие инвестициям факторы. Есть еще одно положение CAРM, которое обычно считают следствием теоремы о разделении: в состоянии равновесия каждый вид ценных бумаг имеет ненулевую долю в касательном портфеле, а структура касательного портфеля повторяет структуру рыночного портфеля в соответствии с долями капитализации ценных бумаг. Обоснованием служит следующее рассуждение: если касательный портфель одного инвестора не включает какую-то бумагу, это означает, что ее стараются продать все (так как инвесторы приобретают одинаковые по структуре рисковые составляющие своих портфелей), тогда рыночный курс этой бумаги под давлением избыточного предложения будет падать, а ожидаемая доходность соответственно расти - до тех пор, пока цена не станет равновесной, а доля в касательном портфеле - отличной от нуля. Противоположные события будут происходить при попытке инвесторов (всех одновременно) увеличить долю какой-то бумаги в рисковой части вложений.

На основе последнего утверждения и используя (2.11) можно записать выражение для ожидаемой доходности финансовых средств любого инвестора в состоянии равновесия рынка:

,                                                       (2.22)

где, как и ранее, - доходность и риск среднерыночного (касательного)      портфеля,

 - доходность безрисковых активов

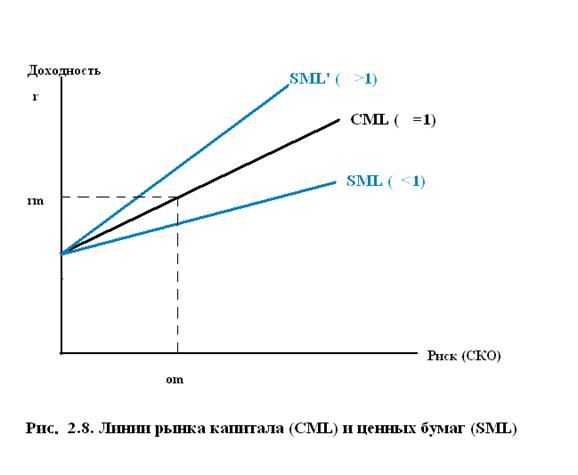
 (2.22) описывает эффективный фронт Тобина (рис.2.8) и получило название уравнение рынка капитала (Capital Market Line - CML). При этом величина

равна тангенсу угла наклона CML к оси ординат и отражает увеличение доходности при увеличении риска на единицу, т.е. предельную доходность риска вложений рынка при наличии рисковых и безрисковых активов. Поскольку CML касается эффективного фронта Марковица в точке 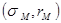, можно выразить тангенс наклона касательной через выражение, описывающее фронт Марковица. Это выражение получено в [Гр] и имеет вид:

,

где 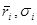 относятся к любой из ценных бумаг портфеля,

- коэффициент корреляции доходности этой ценной бумаги и портфеля в целом.

Приравнивая правые части двух последних выражений, можно получить выражение для ожидаемой доходности любой ценной бумаги в оптимальном портфеле:

 ,                                  (2.23)

которое называется уравнением линии рынка ценных бумаг (Security Market Line - SML) и с учетом (2.13) может быть переписано с использованием коэффициента   :

.                                    (2.24)

Разность  называют премией за недиверсифицированный риск держания рыночного портфеля, соответственно разность  - премия за риск держания отдельноого рискового актива, а бета показывает вклад каждой ценной бумаги в риск рыночного портфеля.

Сравнение выражений для CML и SML показывает, что эти линии на плоскости совпадают только при . При  линия SML проходит выше, а при 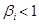 - ниже линии CML (рис.2.8). В любом случае активы с большим риском должны обеспечивать пропорционально большую доходность. Таким образом, если портфель эффективен, связь между ожидаемой доходностью каждой акции и ее предельным вкладом в портфельный риск должна быть прямолинейной. Верно и обратное: если прямолинейной связи нет, портфель не является эффективным.

 

Используя уравнение SML, можно определить факт недооценки или переоценки ценной бумаги (например, акции) не только по ее доходности, но и сравнением ее действительного курса и курса в соответствии с равновесной ценой риска, который обозначим через . Пусть ожидаемая в конце некоторого будущего периода цена акции (учитывая дивидентный доход) равна . Приравнивая выражения доходности по определению и по уравнению SML, получим:

,

откуда следует известная формула дисконтирования по безрисковой доходности, увеличенной на рисковую надбавку:

.

 

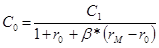Обобщая изложенное, можно считать САРМ макроэкономическим обобщением теории Марковица, позволяющим установить соотношения между доходностью и риском актива для равновесного рынка. При этом важным оказывается тот факт, что при выборе оптимального портфеля инвестор должен учитывать не "весь" риск, связанный с активом (риск по Марковицу), а только недиверсифицируемую его часть. Эта часть риска актива тесно связана с общим риском рынка в целом и количественно представляется коэффициентом "бета", введенным Шарпом в его однофакторной модели. Остальная часть (несистематический, или диверсифицируемый риск) устраняется выбором соответствующего оптимального портфеля. Характер связи между доходностью и риском имеет вид линейной зависимости. Если инвесторы не располагают какой-либо дополнительной информацией, им следует держать такой же портфель акций, как и у других - т.е. рыночный портфель ценных бумаг.

В 1977 г. эта теория подверглась критике в работах Ричарда Ролла. Ролл высказал мнение, что САРМ следует отвергнуть, поскольку она в принципе не допускает эмпирической проверки. Существует достаточно много возражений против обоснованности положений CAPM, самыми спорными из них считаются [4] предположения:

1. Гипотеза эффективного рынка и связанная с ней модель "случайного блуждания" рыночных цен активов

2.  Возможность на практике определить рыночный портфель, который по смыслу должен включать не только абсолютно все ценные бумаги, но и товары длительного пользования, инвестиции в образование (в "человеческий" капитал), недвижимость, драгоценные металлы и другие ценности.

3. Существование безрисковых активово и возможность неограниченного заимствования по ставке безрисковой доходности.

 Несмотря на это, САРМ остается самой значительной и влиятельной современной финансовой теорией. Практические руководства по финансовому менеджменту в части выбора стратегии долгосрочного инвестирования основываются исключительно на САРМ, но используют различные приближения лежащих в ее основе понятий. Укажем два направления таких модификаций, которые в [4] названы обобщениями (обобщенными версиями) САРМ.

Возможность получать кредит по безрисковой ставке на практике имеет только государство, для других инвесторов эта ставка выше, поэтому эффективный фронт изменяется и приобретае вид кривой на рис.2.9, при этом участок  соответствует распределению средств инвестора между портфелем А и безрисковым активом с доходностью , участок АВ - это участок эффективного фронта Марковица, а прямая BL означает получение кредита по ставке и инвестирование всех средств в портфель В. Существенно, что инвестор в этих случаях выбирает различные по структуре портфели рисковых активов. На практике вместо кривой  используют прямую , где  означает доходность гипотетического безрискового актива и определяется по специальным методикам. Новая  имеет более пологий наклон, чем теоретическая, что означает меньшую цену среднерыночного риска.

 

Другим направлением модификаций САРМ для практического применения являются различные представления рыночного портфеля совокупностью фондовых индексов и других факторов. Конечная цель построения таких моделей - получение коэффициентов  активов, позволяющих по возможности точно описывать реальное поведение доходности ценных бумаг. Обзор методических подходов к решению этой задачи приводится в [4]. В западной практике такого рода деятельность осуществляется на коммерческой основе специальными службами, наиболее известны из них BARRA, R&R, Morningstar.

 

Выводы

1. Основой современной теории инвестиций, частью которой является портфельная теория, является теоретико-вероятностная формализация понятия доходности и риска. Лишь применение вероятностных методов позволило существенно продвинуться в исследовании влияния риска на принятие инвестиционных решений.

2. Не существует универсальной меры риска портфеля, учитывающей и обобщающей все возможные субъективные оттенки этого понятия. Среди различных измерителей риска наибольшее распространение и в теории, и на практике получила дисперсия (СКО) доходности портфеля, что не исключает, однако, использование других измерителей.

3. Инвестор выбирает оптимальный портфель из портфелей, составляющих эффективное множество, это множество приобретает вид прямой линии при наличии безрисковых активов.

4. Модель САРМ является макроэкономическим обобщением теории Марковица и Тобина, позволяющим установить линейный вид соотношения между доходностью и риском актива для равновесного рынка.

5. На практике используются модифицированные версии САРМ, использующие различные приближения лежащих в ее основе понятий Но никакая модель не в состоянии учесть все действующие факторы.

Литература

1. Шведов.А.С. Теория эффективных портфелей ценных бумаг. - М., Изд-во ГУ ВШЭ, 1999.

2. Френк Дж. Дерфлер. Вездесущие сети./ PC Magazine Rus, N9, 1999. - стр. 39-52.

3. Первозванский А.А., Первозванская Т.Н. Финансовый рынок: расчет и риск.-М., Инфра-М,- 1994.

4. Уильям Ф. Шарп, Гордон Дж. Александер, Джеффри В. Бейли. Инвестиции. - М., Инфра-М, 1997.

5. Michalovski W., Ogryczak W. Extending MAD Portfolio Optimization Model to Incorporate Downside Risk Aversion. / IIASA, IR-98-041, June 1998./ http://www.iiasa.ac.at/Publications/Documents/IR-98-041.pdf

6. Halme M., Korhonen P. Restricting Weights in Value Efficiency Analysis. / IIASA, IR-98-104, December 1998./ http://www.iiasa.ac.at/Publications/Documents/IR-98-104.pdf

7. William F. Sharpe. Asset Allocation: Management Style and Performance Measurement./ Journal or Portfolio Management, Winter 1992, pp. 7-19.

8. Susmaga R., Michalovski W. Identifying Regularities in Stock Portfolio Tilting. / IIASA, IR-97-66, September 1997.

9. Ковалев В.В. Финансовый анализ. Управление капиталом, выбор инвестиций, анализ отчетности. - М. 1996.

10. Четыркин Е.М. Методы финансовых и коммерческих расчетов.- М. 1996.

11. Карпиков Е.И., Федоров А.А. Основные постулаты классической теории портфельных инвестиций. // http://www.mfc.ru/ecc/bulletin/002/inv-theor.html.

12. Гальперин В.М., Гребенников П.И., Леусский А.И., Тарасевич Л.С. Макроэкономика. - СПб., Изд-во СПбГУЭФ, 1997.

13.  Стратегия активного управления портфелем инвестиций. Система APMS. / http://www.eerc.ru.

14. Терри Дж. Уотшем, Кейт Паррамоу. Количественные методы в финансах.- М.: Финансы, 1999.

15. Ричард Дж.Тьюлз, Эдвард С. Бредли, Тэд М. Тьюлз. Фондовый рынок. - М., Инфра-М, 1999.

16. Лесин В.В., Лисовец Ю.П. Методы оптимизации. - М., Изд-во МАИ, 1998.

17. Гилл Ф., Миррей У., Райт М. Практическая оптимизация. - М.,Мир,1985.

18. Химмельблау Д. Прикладное нелинейное программирование. - М.,Мир, 1975.

 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: