 |
Автоматизация решения задачи
|
|
|
|
Власов В.И. Шарипов О.А.
Сборник задач
По линейному программированию
Методические указания
для самостоятельной работы по курсу
“Математическое моделирование и планирование процессов”
Москва 2011 г.
Задача линейного программирования
Линейное программирование - раздел математического программирования, в котором изучаются методы нахождения условных экстремумов линейных функций многих переменных при наличии дополнительных линейных ограничений на эти переменные, имеющих форму неравенств.
Задача линейного программирования: определить такие значения переменных xj, которые обращают линейную целевую функцию этих переменных в экстремум
 , j = 1 … n
, j = 1 … n
при условии выполнения линейных ограничений-неравенств, накладываемых на эти переменные
 , i = 1 … m, m ≥ n.
, i = 1 … m, m ≥ n.
Метод решения задач линейного программирования
Наиболее эффективным методом решения задачи линейного программирования является симплекс-метод. При решении задачи линейного программирования этим методом:
1) Ограничения-неравенства приводят к одному виду. Если критерием оптимальности является максимум целевой функции, то ограничения-неравенства должны иметь вид
 ,
,
а если критерием оптимальности является минимум целевой функции, то ограничения неравенства приводят к виду
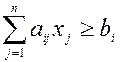 .
.
Переход от одного вида ограничений к другому осуществляется путем изменения знаков коэффициентов aij и свободных членов bi на противоположные.
2) Систему линейных ограничений-неравенств заменяют системой линейных ограничений-равенств путем введения дополнительных переменных yi. При этом свободный член целевой функции полагают равным нулю
|
|
|
 ,
,
 .
.
3) Дополнительные переменные yi выражают через основные xj
 ,
,

и полагают все основные переменные xj равными нулю (базисное решение). Однако это решение не оптимально.
4) Для нахождения оптимального решения необходимо поменять местами n основных переменных xj с равным количеством дополнительных переменных yi, т.е. перевести n дополнительных переменных yi в базисные, равные нулю.
Для этого поочередно в каждом столбце коэффициентов aij определяют разрешающий элемент apq, т.е. положительный элемент столбца, имеющий максимальное отношение к абсолютной величине свободного члена
aij / | bi | = max.
и меняют местами основную переменную xj=q и соответствующую дополнительную переменную yi=p. Полученное значение xj=q подставляют в остальные уравнения.
Задача считается решенной, если в строке целевой функции, не считая свободного члена, нет ни одного положительного элемента (признак оптимальности).
Если после перевода всех основных переменных из базиса в строке целевой функции есть положительный элемент, то соответствующую дополнительную переменную переводят из базисной в свободную, а свободную в базисную, т.е. меняют местами две дополнительные переменные.
Примеры решения задачи
Пример 1.
Задача: Требуется определить максимум функции F = x1 + x2, при условии выполнения следующих ограничений:
x1 + 2 x2£ 6;
2 x1 + x2£ 3;
x1 - 2 x2≥ - 1.
Решение. Приводим ограничения-неравенства к одному виду
x1 + 2 x2£ 6;
2 x1 + x2£ 3;
- 1 x1 + 2 x2£ 1.
Заменяем ограничения-неравенства уравнениями, вводя дополнительные переменные y, и полагаем свободный член в целевой функции равным нулю
x1 + 2 x2 + y1 = 6;
2 x1 + x2 + y2 = 3;
- x1 + 2 x2 + y3 = 1;
x1 + x2 + y4 = 0.
Выражаем значения дополнительных переменных y через основные x
y1 = 6 - (x1 + 2 x2);
y2 = 3 - (2 x1 + x2);
y3 = 1 - (- x1 + 2 x2);
y4 = 0 - (x1 + x2).
Находим разрешающий элемент в первом столбце коэффициентов (вторая строка) и меняем местами основную переменную x1 и дополнительную переменную y2
|
|
|
2 x1 = 3 - (y2 + x2)
или
x1 = 1,5 - 0,5 y2 - 0,5 x2.
Подставляем это значение в остальные уравнения
y1 = 6 - (1,5 - 0,5 y2 - 0,5 x2 + 2 x2);
x1 = 1,5 - (0,5 y2 + 0,5 x2);
y3 = 1 - (-1,5 + 0,5 y2 + 0,5 x2 + 2 x2);
y4 = 0 - (1,5 - 0,5 y2 - 0,5 x2 + x2).
Тогда система уравнений примет вид
y1 = 4,5 - (-0,5 y2 + 1,5 x2);
x1 = 1,5 - (0,5 y2 + 0,5 x2);
y3 = 2,5 - (0,5 y2 + 2,5 x2);
y4 = -1,5 - (-0,5 y2 + 0,5 x2).
Теперь находим разрешающий элемент во втором столбце (третья строка) и меняем местами основную переменную x2 с дополнительной переменной y3
2,5 x2 = 2,5 - (0,5 y2 + y3)
или
x2 = 1 - 0,2 y2 - 0,4 y3.
Подставляем это значение в остальные уравнения.
y1 = 4,5 - (-0,5 y2 + 1,5 - 0,3 y2 - 0,6 y3);
x1 = 1,5 - (0,5 y2 + 0,5 - 0,1 y2 - 0,2 y3);
x2 = 1,0 - (0,2 y2 + 0,4 y3);
y4 = -1,5 - (-0,5 y2 + 0,5 - 0,1 y2 - 0,2 y3).
Тогда система уравнений примет вид
y1 = 3 - (-0,8 y2 - 0,6 y3);
x1 = 1 - (0,4 y2 - 0,2 y3);
x2 = 1 - (0,2 y2 + 0,4 y3);
y4 = -2 - (-0,6 y2 - 0,2 y3).
Так как коэффициенты перед дополнительными переменными y2 и y3 в строке целевой функции имеют отрицательные значения, то оптимальное решение имеется
x1 = 1 x2 = 1.
Пример 2.
Задача: Требуется определить максимум функции F = x2 при условии выполнения следующих ограничений:
x1 + 4 x2 £ 16;
x1 - 2 x2 ³ - 2;
x1 + 2 x2 £ 6;
x1 £ 3.
Решение. Приводим ограничения-неравенства к одному виду
x1 + 4 x2 £ 16;
- x1 + 2 x2 £ 2;
x1 + 2 x2 £ 6;
x1 £ 3.
Заменяем ограничения-неравенства уравнениями, вводя дополнительные переменные y и полагая свободный член в целевой функции, равным нулю.
x1 + 4 x2 + y1 = 16;
- x1 + 2 x2 + y2 = 2;
x1 + 2 x2 + y3 = 6;
x1 + y4 = 3;
x2 + y5 = 0.
Выражаем значения дополнительных переменных y через основные x
y1 = 16 - (x1 + 4 x2);
y2 = 2 - (-x1 + 2 x2);
y3 = 6 - (x1 + 2 x2);
y4 = 3 - (x1);
y5 = 0 - (x2).
Находим разрешающий элемент в первом столбце (четвертая строка) и меняем местами основную переменную x1 с дополнительной переменной y4
x1 = 3 - y4.
Подставляем это значение в остальные уравнения
y1 = 16 - (3 - y4 + 4 x2);
y2 = 2 - (-3 + y4 + 2 x2);
y3 = 6 - (3 - y4 + 2 x2);
y4 = 3 - (x1);
y5 = 0 - (x2).
Тогда система уравнений примет вид
y1 = 13 - (-y4 + 4 x2);
y2 = 5 - (y4 + 2 x2);
y3 = 3 - (-y4 + 2 x2);
x1 = 3 - (y4);
y5 = 0 - (x2).
Теперь находим разрешающий элемент во втором столбце (третья строка) и меняем местами основную переменную x2 и дополнительную переменную y3
2 x2 = 3 - (-y4 + y3)
или
x2 = 1,5 + 0,5 y4 - 0,5 y3.
Подставляем это значение в остальные уравнения
y1 = 13 - (- y4 + 6 + 2 y4 - 2 y3);
y2 = 5 - (y4 + 3 + y4 - y3);
x2 = 1,5 - (-0,5 y4 + 0,5 y3);
x1 = 3 - (y4);
y5 = 0 - (1,5 + 0,5 y4 - 0,5 y3).
|
|
|
Тогда система уравнений примет вид
y1 = 7 - (y4 - 2 y3);
y2 = 2 - (2 y4 - y3);
x2 = 1,5 - (-0,5 y4+ 0,5 y3);
x1 = 3 - (y4);
y5 = -1,5 - (0,5 y4 - 0,5 y3).
Так как в строке целевой функции коэффициент перед дополнительной переменной y4 положительный, то решение x1 = 3 и x2 = 1,5 не оптимально.
Поэтому в столбце коэффициентов перед y4 (вторая строка) находим разрешающий элемент и относительно его меняем местами дополнительные переменные y2 и y4
2 y4 = 2 - (y2 - y3)
или
y4 = 1 - 0,5 y2 + 0,5 y3.
Подставляем это значение в остальные уравнения
y1 = 7 - (1 - 0,5 y2 + 0,5 y3 - 2 y3);
y4 = 1 - (0,5 y2 - 0,5 y3);
x2 = 1,5 - (-0,5 + 0,25 y2 - 0,25 y3 + 0,5 y3);
x1 = 3 - (1 - 0,5 y2 + 0,5 y3);
y5 = -1,5 - (0,5 - 0,25 y2 + 0,25 y3 - 0,5 y3).
Тогда система уравнений примет вид
y1 = 6 - (-0,5 y2 - 1,5 y3);
y4 = 1 - (0,5 y2 - 0,5 y3);
x2 = 2 - (0,25 y2 + 0,25 y3);
x1 = 2 - (-0,5 y2 + 0,5 y3);
y5 = -2 - (-0,25 y2 - 0,25 y3).
Так как коэффициенты перед дополнительными переменными y2 и y3 в строке целевой функции отрицательные, то оптимальное решение найдено.
x1 = 2 x2 = 2.
Автоматизация решения задачи
Код программы на языке программирования Just BASIC.
‘ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
‘ ВВОД ДАННЫХ
INPUT M
INPUT N
DIM A(M,N), B(M), C(M), X(M),Y(N)
FOR I=1 TO M
FOR J=1 TO N
INPUT A(I,J)
NEXT J
INPUT B(I)
NEXT I
' Перестроение переменных
FOR L = 1 TO N
P = L
GOSUB [OpRazEl] ' Вызов функции замены переменных
FOR J = 1 TO N
V = A(L, J)
A(L, J) = A(K, J)
A(K, J) = V
NEXT J
W = B(L)
B(L) = B(K)
B(K) = W
NEXT L
IF M <> N + 1 THEN
FOR L = 1 TO N
250 IF A(M, L) >= 0 THEN
P = N + 1
GOSUB [OpRazEl] ' Вызов функции замены переменных
GOTO 250
ELSE
END IF
NEXT L
ELSE
END IF
‘ ВЫВОД РЕШЕНИЯ
FOR I=1 TO N
PRINT B(I)
NEXT I
END
' Процедура определения разрешающего элемента
[OpRazEl]
E = 0
FOR I = P TO M - 1
IF A(I, L) <> 0 THEN
IF B(I) = 0 THEN K = I: EXIT FOR
C(I) = A(I, L) / ABS(B(I))
IF C(I) > E THEN E = C(I): K = I
ELSE
END IF
NEXT I
' Пpисвоение меток
FOR I = 1 TO M
IF I = K THEN
Z = B(I)
FOR J = 1 TO N
IF J = L THEN
S = A(I, J)
ELSE
Y(J) = A(I, J)
END IF
NEXT J
ELSE
FOR J = 1 TO N
IF J = L THEN X(I) = A(I, J)
NEXT J
END IF
NEXT I
' Преобразование матрицы
FOR I = 1 TO M
IF I = K THEN
B(I) = Z / S
FOR J = 1 TO N
IF J = L THEN
A(I, J) = 1 / S
ELSE
A(I, J) = Y(J) / S
END IF
NEXT J
ELSE
B(I) = B(I) - X(I) * Z / S
FOR J = 1 TO N
IF J = L THEN
A(I, J) = -X(I) / S
|
|
|
ELSE
A(I, J) = A(I, J) - X(I) * Y(J) / S
END IF
NEXT J
END IF
NEXT I
Варианты задач линейного программирования
Определить такие значения переменных x1 и x2, которые обращают линейную функцию этих переменных Fo в экстремум, при условии выполнения линейных ограничений неравенств, накладываемых на эти переменные.
Задание №1
| Задача 1.1 | Задача 1.2 | |||||||||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.3 | Задача 1.4 | |||||||||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.5 | Задача 1.6 | |||||||||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≤ | |||||||||
| x2 | = | max | x2 | = | min | |||||||||||
| Задача 1.7 | Задача 1.8 | |||||||||||||||
| – | x1 | + | x2 | ≥ | – | x1 | + | x2 | ≤ | |||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||
| x1 | = | max | x1 | = | min | |||||||||||
| Задача 1.9 | Задача 1.10 | |||||||||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.11 | Задача 1.12 | |||||||||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.13 | Задача 1.14 | |||||||||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.15 | Задача 1.16 | |||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.17 | Задача 1.18 | |||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.19 | Задача 1.20 | |||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.21 | Задача 1.22 | |||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.23 | Задача 1.24 | |||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||
| Задача 1.25 | Задача 1.26 | |||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min |
Задание №2
|
|
|
| Задача 2.1 | Задача 2.2 | |||||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≤ | |||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||||
| Задача 2.3 | Задача 2.4 | |||||||||||||||||
| x1 | – | x2 | ≥ | x1 | – | x2 | ≤ | |||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||||
| x1 | ≥ | x1 | ≥ | |||||||||||||||
| x2 | = | max | x2 | = | min | |||||||||||||
| Задача 2.5 | Задача 2.6 | |||||||||||||||||
| x1 | + | x2 | ≥ | x1 | + | x2 | ≤ | |||||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||||
| x1 | ≤ | x1 | ≤ | |||||||||||||||
| x1 | – | x2 | = | max | x1 | – | x2 | = | min | |||||||||
| Задача 2.7 | Задача 2.8 | |||||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≥ | |||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||||
| x1 | ≤ | x1 | ≤ | |||||||||||||||
| x2 | = | max | x2 | = | min | |||||||||||||
| Задача 2.9 | Задача 2.10 | |||||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||||
| x1 | – | x2 | ≥ | x1 | – | x2 | ≥ | |||||||||||
| x1 | ≤ | x1 | ≤ | |||||||||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | min | |||||||||
| Задача 2.11 | Задача 2.12 | |||||||||||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≥ | |||||||||
| x1 | – | x2 | ≥ | x1 | – | x2 | ≥ | |||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≥ | |||||||||
| x1 | – | x2 | = | max | x1 | – | x2 | = | min | |||||||
| Задача 2.13 | Задача 2.14 | |||||||||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≤ | |||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≤ | |||||||||
| x1 | + | x2 | ≥ | x1 | + | x2 | ≥ | |||||||||
| x1 | – | x2 | ≤ | x1 | – | x2 | ≤ | |||||||||
| x1 | ≤ | x1 | ≤ | |||||||||||||
| x1 | + | x2 | = | max | x1 | | = | min | ||||||||
| Задача 2.15 | Задача 2.16 | |||||||||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≤ | |||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≤ | |||||||||
| x1 | + | x2 | ≤ | x1 | – | x2 | ≤ | |||||||||
| x1 | – | x2 | ≤ | x1 | ≤ | |||||||||||
| x1 | ≤ | x1 | + | x2 | = | max | ||||||||||
| x2 | = | max | ||||||||||||||
| Задача 2.17 | Задача 2.18 | |||||||||||||||
| x1 | + | x2 | ≥ | x1 | + | x2 | ≥ | |||||||||
| – | x1 | + | x2 | ≤ | – | x1 | + | x2 | ≤ | |||||||
| x1 | + | x2 | ≤ | x1 | + | x2 | ≤ | |||||||||
| x1 | ≤ | x1 | ≤ | |||||||||||||
| x1 | + | x2 | = | max | x1 | + | x2 | = | ||||||||
|
|
|


