 |
Тема занятия 11: Резонанс токов
|
|
|
|
Конспект по дисциплине: «Теория электрических цепей»
(для дневной и заочной формы обучения)
Весенний семестр
Тема занятия 1: Сигналы негармонической формы
Чаще всего в аппаратуре связи используются сигналы негармонической формы, то есть сигналы, изменяющиеся не по закону синуса или косинуса, а по более сложным законам. Так называемые, несинусоидальные токи.
Источники несинусоидальных токов:
1) Источники, генерирующие ЭДС несинусоидальной формы;
2) Если последовательно соединено несколько источников синусоидальных ЭДС с кратными частотами;
3) Если в цепи имеется нелинейный элемент, на который подается гармоническое воздействие.
Для расчета цепей при негармоническом воздействии используется теорию рядов Фурье: любую периодическую негармоническую функцию можно разложить на гармонические составляющие с кратными частотами. Расчет цепи производится для каждой составляющей с последующим суммированием.
При сложении двух синусоидальных функций с кратными частотами, получилась периодическая, но не гармоническая функция.
Синусоиды, входящие в ряд Фурье, называются гармониками.
Основная гармоника – это гармоника, частота которой совпадает с частотой негармонического сигнала. Все остальные гармоники, частоты которых в целое число раз больше частоты основной гармоники называются высшими гармониками.
Если частота гармоники равна нулю, то такую гармонику называют нулевой, либо постоянной составляющей.
Существует две формы записи ряда Фурье:
1. Ряд Фурье с начальными фазами
- постоянная составляющая
– основная
Вместо А может быть ток, напряжение, ЭДС.
Как правило амплитуда Аm1 будет больше всех остальных (высших) гармоник.
|
|
|
В технике связи применяется несинусоидальные напряжения и токи, которые содержат или не содержат постоянную составляющую, также могут содержать гармоники, у которых нет начальных фаз.
2. Ряд Фурье с нулевыми начальными фазами (без начальных фаз):
Таким образом, ряд Фурье с начальными фазами можно заменить рядом, содержащим косинусоиды и синусоиды без начальных фаз.
Известно, что
Если интегрировать ряд Фурье, содержащий все гармоники, то результат будет равен постоянной составляющей. Если в ряде Фурье не будет постоянной составляющей, то при интегрировании ряда Фурье результат равен нулю.
Найдем: 
По аналогичной формуле можно найти амплитуды любых гармоник.
1.1 Симметричные несинусоидальные кривые
1. Кривые, симметричные относительно оси Оx:
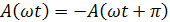
Ряд Фурье содержит синусоидальные составляющие с начальными фазами и нечетными номерами:
Если отрицательная часть сдвинуть на полпериода влево и расположить ее под положительной частью кривой, то отрицательная часть будет зеркально отображена положительной. У несинусоидальных кривых, симметричных относительно оси абсцисс, нет постоянной составляющей, и четных гармоник, поэтому ряд Фурье имеет следующий вид:
2 Кривые симметричные относительно оси Oy:
Ряд Фурье содержит постоянную составляющую и косинусоидальные составляющие:
Кривые содержат косинусоидальные составляющие с нулевыми начальными фазами и постоянной составляющей.
3 Кривые, симметричные относительно начала координат:
Ряд Фурье содержит только синусоидальные
составляющие без начальных фаз:
Сигналы прямоугольной и треугольной формы обладают двумя видами симметрии:
1) Симметричные относительно оси Оx (отсутствуют все четные гармоники);
2) Симметричные относительно начала координат (пропадают все косинусоидальные составляющие, по этому данный сигнал содержит только нечетные синусоиды с нулевыми начальными фазами).
|
|
|
Поэтому данные сигналы состоят из нечетных синусоид с нулевыми начальными фазами.
1.2 Спектральное представление сигналов.
Спектр – совокупность синусоидальных составляющих, образующих негармонический сигнал. Это зависимость составляющих ряда Фурье от частоты.
Вместо временных составляющих рисуют вертикальную линию, длина которой пропорциональна амплитуде, а расположение по оси Оx определяется частотой гармоники.
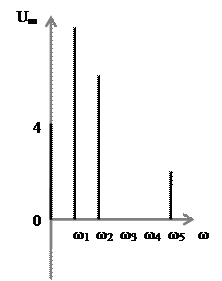
- это амплитудный спектр сигнала, так как откладываются амплитуды гармоник.
Существуют и фазные спектры (по горизонтальной оси откладываются частоты, а по вертикальной фазы гармонических составляющих).
Так как ряд любого периодического сигнала состоит из гармонических составляющих, отличающихся в целое число раз от частоты первой гармоники, то спектральные линии находящиеся на расстоянии Δf друг от друга, где
Δf – частотный интервал, равный частоте первой гармоники.
Спектр, состоящий из отдельных линий, называется линейчатым или дискретным.
Спектр синусоиды:
Если изменяется частота синусоиды, то линия смещается влево или вправо, но остается одна.
Спектр треугольного сигнала:
Сигнал состоит из гармонических составляющих с нечетными номерами, амплитуды которых уменьшаются пропорционально квадрату номера гармоники.
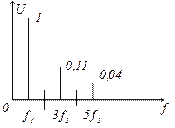
У сигналов прямоугольной формы со скважностью 2 амплитуды нечетных гармонических составляющих уменьшаются пропорционально номерам гармоник, амплитуды гармоник с нечетными номерами равны нулю.
Выводы: периодические сигналы имеют дискретные спектры, а непериодические – сплошной спектр. Чтобы построить спектр любого периодического сигнала, необходимо знать закон мгновенных значений, то есть ряд Фурье для данного сигнала.
Тема занятия 2: Расчет цепи при воздействии негармонических
периодических сигналов.
При расчете цепей при негармоническом воздействии используется принцип независимого действия отдельных гармоник на данную цепь.
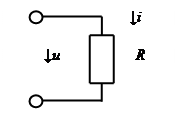
Используется
R-цепь
Сопротивление R не зависит от частоты, ток и напряжение совпадают по фазе, отсюда следует, что форма тока повторяет форму напряжения. Для нахождения тока используется закон Ома.
|
|
|
Чтобы найти ток необходимо каждую гармонику напряжения разделить на величину сопротивления, а фазу оставить неизменной, так как ток и напряжение в цепи с R совпадают по фазе.
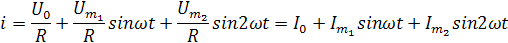
Пример:R=20 Ом;
U=200+160sinwt+80sin(3wt-90°)+40sin(5wt+90°).
Найти i.
I=10+8sinwt+4sin(3wt-90°)+2sin(5wt+90°).
 |
L-цепь
С ростом частоты индуктивное сопротивление увеличивается, поэтому ток низких частот пройдет хорошо, ток верхних – плохо. Форма тока будет более сглаженной, то есть приближенной к синусоиде.
Для нахождения тока необходимо:
1. Рассчитаем сопротивление для каждой гармоники:
2. По закону Ома для цепи с индуктивностью определяем амплитуды тока соответствующих гармоник:
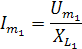
, для общего случая
3. Записать выражения мгновенных значений тока каждой гармоники, учитывая что в цепи с индуктивностью отстает от напряжения на 90°:
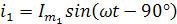
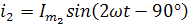
4. Записать общий ток, как сумму токов каждой гармоники:
.
Пример:X3=30 Ом
U=90sinwt+30sin(3wt+45°)+10sin(5wt+80°)
Найти i.
C-цепь
С увеличением частоты реактивное сопротивление уменьшается, значит токи высокой частоты пройдут хорошо, а низкой – плохо. Поэтому форма тока будет более «несинусоидальной», чем форма напряжения.
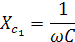
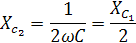
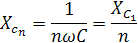
По закону Ома определяется максимальное значение тока:
Записываем уравнение тока каждой гармоники, учитывая, что ток опережает напряжение на 90°.
i=i1+i2=Im sin(wt+90°)+Im sin(2wt-25°)
Пример: С=100 мкФ
I=25sin (1000t-75°)+8sin(2000t+30°)+2sin(3000t+90°)
Решение:
X1=1/w1c=10 Ом X2=1/w2c= 5 Ом X3= 1/w3c= 3,3 Ом
Um1=Im1X1 =250 B Um2=Im2X2=40 B Um3=Im3X3=6,7 B
U=250 sin(1000t-165°)+40 sin(2000t-60°)+6,7 sin(3000t)
2.1 Действующие значения несинусоидальных токов и напряжений.
Мощность.
Действующее значение любого периодического сигнала определяется:
Подставив вместо напряжения и тока соответствующие ряды и произвести действия, получим:
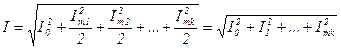
U0 и I0 – постоянные составляющие.
Umk, Imk – максимальные значения гармонических составляющих.
Umk= Umk/√2 и Imk= Imk/√2 - действующие значения соответствующих гармоник.
|
|
|
В цепях с несинусоидальными токами амплитуды показывают действующее значение.
Действительное значение несинусоидального тока – постоянный ток, который за время равное Т, выделяет в резисторе такое же количества тепла, что и несинусоидальный ток за то же время.
Коэффициент искажений – отношение геометрической суммы амплитуд высших гармоник к амплитуде первой гармоники
Коэффициент амплитуды – отношение максимального значения сигнала к действующему значению сигнала
Для синусоидальных сигналов kа=U√2 /U=√2.
Задача:
В цепи последовательно соединены резистор и конденсатор. R=10 Ом, С=106 мкФ, f= 50 Гц.
U=141sinwt+70,7sin3wt+42,4sin5wt.
Найти: i, I,U,ka,ku, спектр u,i.
Тема занятия 3: Соединение фаз генератора и потребителя звездой.
Трехфазный генератор в отличие от однофазного имеет три рабочие обмотки, сдвинутые между собой по окружности на 120°. В них индуцируются равные ЭДС одинаковой частоты, сдвинутые по фазе одна относительно другой на 120°.
Мгновенные значения ЭДС:
eA=Emsinωt
eB=Emsin(ωt-120°)
eС=Emsin(ωt-240°)
В комплексной форме: EA=Eej0°, EB=Ee-j120°, EС=Ee-j240°.
Фазой трехфазной системы называется часть трехфазной системы электрических цепей, в которой может протекать один из токов трехфазной системы.
Обмотки трехфазного генератора называются фазами генератора.
Начало фазных обмоток называется А, В, С; конец – x, y, z.
Если три конца обмоток генератора соединены в одну общую точку (узел), которая называется нулевой, то такое соединение называется звездой.
За начало обмоток принимают тот конец, к которому направлена положительная ЭДС.
К генератору подсоединяется нагрузка
Соединим звезду генератора со звездой потребителя.
Провод, соединяющий центральные точки генератора и потребителя называется нейтральным. (- - - - -)
Три провода, отходящие от начала обмоток генератора, называются линейным проводом.
Напряжение между линейным проводом называется линейным, а токи, текущие в них – линейными токами.
При такой схеме ток в нейтральном проводе равен геометрической сумме токов трех потребителей, и поскольку токи трех фаз при симметричной нагрузке (номиналы сопротивлений потребителей Z 1, Z 2, Z 3 одинаковы) генератора равны по величине и сдвинуты по фазе относительно друг друга на 120°, их сумма равна 0.
IN=IAej0+IBe-j120°+ICej120=0
Поэтому нейтральный провод называют нулевым.
Поэтому при симметричной нагрузке фаз нейтральный провод не нужен, т.к. ток в нем равен 0.
Напряжение и токи фаз называются фазными.
Здесь UА, UВ, UС – фазные напряжения. IА=Iф.
По второму закону Кирхгоффа:
U AB= U A- U B
U BC= U B- U C
U AC= U A- U C
|
|
|
Линейные напряжения равны разности векторов фазных напряжений.
, где UAB=UЛ, а UB=UФ
. Следовательно 
IЛ=IФ При соединении звездой.
Мощность трехфазной системы равна сумме мощностей каждой фазы
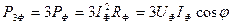
3.1 Порядок расчета
Дано UЛ=UAB=UBC=UAC
ZA=ZB=ZC
Найти: фазные ток и напряжение, ток линейный, углы сдвига по фазе, активную, реактивную и полную мощности фаз и всей системы.
Решение:
1. Рассчитываем фазные напряжения:
UФ=UЛ/ 
2. Определим фазные и линейные токи:
3 Определим углы сдвига по фазе между напряжением и током:
4 Определим активную мощность одной фазы:
, Вт
5 Определим реактивную мощность одной фазы:
, Вар
6 Определим полную мощность фазы:
7 Определим активную мощность всей системы:
8 Определим реактивную мощность всей системы:
9 Полная мощность всей системы:
Задача:
Фазы генератора и потребителя соединены по системе звезда, фазный ток составляет 1,27 А, активное сопротивление одной фазы 80 Ом, реактивное сопротивление одной фазы 60 Ом. Найти линейные напряжение и ток, фазное напряжение, угол сдвига по фазе между напряжением и током, полную, активную, реактивную мощности всей системы.
Тема занятия 4:Соединение фаз генератора и потребителя треугольником.
Связанную трехфазную систему можно осуществить и при соединении обмоток генератора и потребителя треугольником. Для этого начала трех фаз соединяются с концами предыдущих фаз. Линейные провода выводятся из точек соединения фаз. Таких точек три, следовательно система трехпроводная. При этом образовывая замкнутый контур.
При отсутствии подключенных к генератору потребителей ток равен нулю, так как сумма трех комплектов ЭДС равнв нулю(ЭДС сдвинуты на 1200 друг относительно друга).
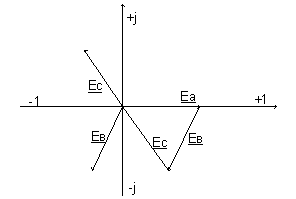
При сложении трех векоров получается замкнутый треугольник, то есть геометрическая сумма векторов равна нулю.
Вольтметр, включенный между двумя линейными проводами, покажет линейное напряжение, но это напряжение UАВ подается от одной обмотки фазы генератора и, следовательно, при соединении обмоток генератора треугольником.
UЛ=UФ
При соединении обмоток генератора треугольником от него можно получить только одно напряжение – фазное
.
Схема соединения треугольником:
где IA, IB,IC –линейные токи.
IAB,IBC,IAC–фазные токи.
Задача: В треугольник соединены три приемника, которые имеют следующие сопротивления:
RA=6 Ом, RB=12 Ом, RC=10 Ом.
XA =8 Ом, XB =9 Ом, XC=15 Ом.
Определить активную мощность трехфазной системы, если напряжение сети 220 В.
Тема занятия 5: Колебательный контур.
5.1 Идеальный колебательный контур.
Колебательный контурназывается идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.
Рассмотрим физические процессы в следующей цепи:
1 Ключ стоит в положении 1 Конденсатор начинает заряжаться, от источника напряжения и в нем накапливается энергия электрического поля, 
т.е.конденсатор становится источником электрической энергии.
2. Ключ в положении 2. Конденсатор начнет разряжаться. Электрическая энергия, запасенная в конденсаторе переходит в энергию магнитного поля катушки.
Ток в цепи достигает максимального значения(точка 1).
Напряжение на обкладках конденсатора уменьшается до нуля.
В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся, то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).
Вывод: в цепи LC происходит непрерывное колебание энергии между электрическим и магнитным полями, поэтому такая цепь называется колебательным контуром.
Получившиеся колебания называются свободными или собственными, поскольку они происходят без помощи постороннего источника электрической энергии, внесенной ранее в контур (в электрическое поле конденсатора). Так как емкость и индуктивность идеальны (нет сопротивления потерь) и энергия из цепи не уходит, амплитуда колебаний с течением времени не меняется и колебания будут незатухающими.
Определим угловую частоту свободных колебаний:
Используем равенство энергий электрического и магнитного полей
где ώ угловая частота свободных колебаний.
[ ώ ]=1/с
f0=ώ/2π [Гц].
Период свободных колебаний Т0=1/f.
Частоту свободных колебаний называют частотой собственных колебаний контура.
Из выражения: ώ²LC=1 получим
ώL=1/Cώ, следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.
- характеристические сопротивления.
Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется характеристическим сопротивлением.
5.2 Реальный колебательный контур
Реальный колебательный контур обладает активным сопротивлением, поэтому при воздействии в контуре свободных колебаний энергия предварительно заряженного конденсатора постепенно тратится, преобразуясь в тепловую.
Свободные колебания в контуре являются затухающими, так как в каждый период энергия уменьшается и амплитуда колебаний в каждый период будет уменьшаться.
 |
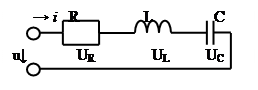Рисунок - реальный колебательный контур.
Угловая частота свободных колебаний в реальном колебательном контуре:
Если R=2…, то угловая частота равна нулю, следовательно свободные колебания в контуре не возникнут.
Таким образом колебательным контуром называется электрическая цепь состоящая из индуктивности и емкости и обладающая малым активным сопротивлением, меньшим удвоенного характеристического сопротивления, что обеспечивает обмен энергией между индуктивностью и емкостью.
В реальном колебательном контуре свободные колебания затухают тем быстрее, чем больше активное сопротивление.
Для характеристики интенсивности затухания свободных колебаний используется понятие «затухание контура» - отношение активного сопротивления к характеристическому.
На практике используют величину, обратную затуханию – добротность контура.
Для получения незатухающих колебаний в реальном колебательном контуре необходимо в течение каждого периода колебаний пополнять электрическую энергию на активном сопротивлении контура в такт с частотой собственных колебаний. Это осуществляется с помощью генератора.
Если подключить колебательный контур к генератору переменного тока, частота которого отличается от частоты свободных колебаний контура, то в цепи протекает ток с частотой равной частоте напряжения генератора. Эти колебания называют вынужденным.
Если частота генератора отличается от собственной частоты контура, то такой колебательный контур является ненастроенным относительно частоты внешнего воздействия, если же частоты совпадают, то настроенным.
Задача: Определить индуктивность, угловую частоту контура, характеристическое сопротивление, если емкость колебательного контура 100 пФ, частота свободных колебаний 1,59 МГц.
Решение:
Тестовые задания:
| Добротность колебательного контура определяется по формуле: | 1) Отношение активного сопротивления к характеристическому 2) Величина обратная затуханию |
| Какие колебания называются свободными | 1) непрерывные колебания энергии между электрическим и магнитным полями 2) колебания, амплитуда которых в каждый период времени уменьшается |
Тема занятия 8: Резонанс напряжений.
Резонанс напряжений – явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением.
Условия возникновения резонанса:
1. Последовательное соединение L и C с генератором переменного тока;
2. Частота генератора должна быть равна частоте собственных колебаний контура, при этом характеристические сопротивления равны;
3. Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.
Полное сопротивление цепи:
=R,
так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение.
При максимальном значении тока напряжение на участках L и C будут большими и равными между собой.
Напряжение на зажимах цепи:
.
Рассмотрим следующие соотношения:
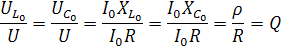, следовательно
.
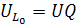
Q – добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура
резонанса.
Пример:
Если добротность равна 100, напряжение на зажимах 1В, то
Uc=Ul=QU =100В,
то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений.
При резонансе, коэффициент передачи равен добротности.
Построим векторную диаграмму напряжения.
 |
Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током.
Рассмотрим энергетический процесс в колебательном контуре:
В цепи имеется обмен энергии между электрическим полем конденсатора и магнитным полем катушки. К генератору энергия катушки не возвращается. От генератора в цепь поступает такое количество энергии, которое тратится на резисторе. Это необходимо для того, чтобы в контуре наблюдались незатухающие колебания. Мощность в цепи только активная.
Докажем это математически:
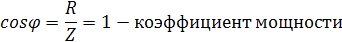
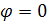
, полная мощность цепи, которая равна активной мощности.
, реактивная мощность.
8.1 Резонансная частота. Расстройка.
В цепи, содержащей реактивные элементы, произойдет резонанс, если цепь имеет резистивный характер:
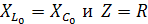
Lώ=l/ώC, следовательно
, угловая резонансная частота.
Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура.
При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуре присутствует расстройка.
Настроить колебательный контур в резонанс можно тремя способами:
1 Изменять частоту генератора, при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура
2 Изменять индуктивность катушки, при частоте питания и емкости const;
3 Изменять емкость конденсатора, при частоте питания и индуктивности const.
Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора.
При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка.
Расстройка – отклонение частоты от резонансной частоты.
Существует три вида расстройки:
1. Абсолютная – разность между данной частотой и резонансной
2. Обобщенная – отношение реактивного сопротивления к активному:
3. Относительная – отношение абсолютной расстройки к резонансной частоте:
При резонансе все расстройки равны нулю, если частота генератора меньше частоты контура, то расстройка считается отрицательной,
Если больше – положительной.
Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты.
8.2 Построение зависимостей X, XL, XC от f.
При резонансе 
реактивные сопротивления равны, следовательно 
.
При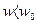 
- цепь носит емкостной характер,
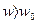- носит индуктивный характер.
Задачи:
1. Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.
Решение:
2. Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.
Решение:
Тестовые задания:
| Отношение реактивного сопротивления к активному это: | А) Абсолютная расстройка; Б) Обобщенная расстройка; В) Относительная расстройка. |
Тема занятия 9: Входные и передаточные АЧХ и ФЧХ последовательного колебательного контура.
9.1 Входные АЧХ и ФЧХ.
В последовательном колебательном контуре:
, где
R – активное сопротивление;
X – реактивное сопротивление.
Учитывая, что
,то
ώ=0 ζ=-∞ Z=∞
ώ=ώ۪۪ 
ζ=0 Z=R
ώ=∞ζ=∞ Z=∞, следовательно график имеет вид: 
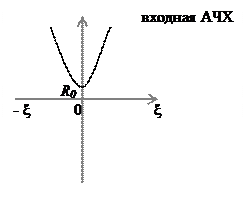
Из графика видно, что контур обладает наименьшим сопротивлением на резонансной частоте, при увеличении расстройки сопротивление увеличивается.
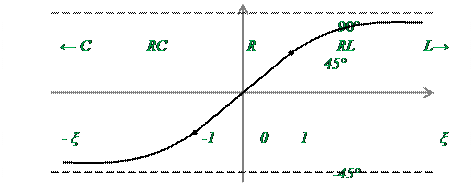
ζ=0 φ=0 R
ζ=1 φ=45° RL
ζ=-1 φ=-45° RC
ζ=∞ φ=90° L
ζ=-∞ φ=-90° C.
Построим график:
На участке ζ=[-1;1]
ФЧХ имеет линейный
характер. 
1. На участке ζ=[-∞;0] - цепь носит активно-емкостной характер;
2. На участке ζ=[0;∞]- цепь носит frnbdyj-индуктивный характер;
3. При ζ=0 - цепь носит активный характер;
9.2 Передаточные АЧХ и ФЧХ
передаточная характеристика АЧХ
 |
ζ=-∞ k=0
ζ=0 k=Q
ζ=∞ k=0
Построим график зависимости:
Разделим k∕kо и получим передаточную
характеристику АЧХ в относительных
единицах, которая имеет вид:
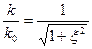
Чтобы построить передаточную ФЧХ необходимо: построить входную ФЧХ, взять её зеркальное ее отображение и сместить на -90°.
На участке ζ=[-1;1] – передаточная ФЧХ носит линейный характер.
9.3 Избирательность и полоса пропускания последовательного контура.
Избирательность – способность контура усиливать напряжения на различных частотах в неодинаковое число раз.
Контур как бы «выбирает» из спектра напряжения на тех частотах, которые близки к резонансной.
Коэффициент передачи по напряжению в последовательном колебательном контуре зависит от частоты, поэтому при подведении на вход контура спектра частот с одинаковыми амплитудами на выходе получается спектр тех же частот, но с различными амплитудами, так как напряжение выхода равно произведению коэффициента передачи и входного напряжения.
|
|
|
