 |
Допускаемые напряжения изгиба
|
|
|
|
Расчет допускаемых напряжений
Допускаемые контактные напряжения
Расчет на усталость рабочих поверхностей зубьев колес при циклических контактных напряжениях базируется на экспериментальных кривых усталости, которые обычно строят в полулогарифмических координатах (рис. 2.1).
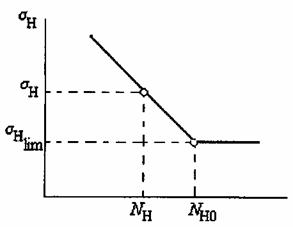
Рис. 2.1
Здесь: 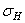 − наибольшее напряжение цикла, NH − число циклов нагружений,
− наибольшее напряжение цикла, NH − число циклов нагружений, 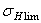 (
( 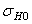 ) − предел выносливости материала, N HG (N H 0) − базовое число циклов (абсцисса точки перелома кривой усталости).
) − предел выносливости материала, N HG (N H 0) − базовое число циклов (абсцисса точки перелома кривой усталости).
Допускаемое контактное напряжение рассчитывают для каждого зубчатого колеса передачи по формуле
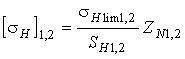 ,
,
где 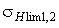 определяют по эмпирическим зависимостям, указанным в табл.2.2;
определяют по эмпирическим зависимостям, указанным в табл.2.2;
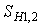 − коэффициент безопасности, рекомендуют назначать SH = 1,1 при нормализации, термоулучшении или объемной закалке зубьев (при однородной структуре материала по всему объему); SH = 1,2 при поверхностной закалке, цементации, азотировании (при неоднородной структуре материала по объему зуба);
− коэффициент безопасности, рекомендуют назначать SH = 1,1 при нормализации, термоулучшении или объемной закалке зубьев (при однородной структуре материала по всему объему); SH = 1,2 при поверхностной закалке, цементации, азотировании (при неоднородной структуре материала по объему зуба);
ZN (KHL) − коэффициент долговечности,
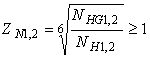 , но 2,6 при SH = 1,1;
, но 2,6 при SH = 1,1;
и 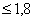 при SH = 1,2.
при SH = 1,2.
Если 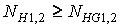 , то следует принимать
, то следует принимать 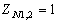 .
.
Коэффициент ZN учитывает возможность повышения допускаемых напряжений для кратковременно работающих передач (при N H < N HG ).
Расчет числа циклов перемены напряжений выполняют с учетом режима нагружения передачи. Различают режимы постоянной и переменной нагрузки. При постоянном режиме нагрузки расчетное число циклов напряжений
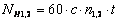 ,
,
где c − число зацеплений зуба за один оборот (для проектируемого одноступенчатого редуктора с = 1);
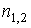 − частота вращения того зубчатого колеса, по материалу которого определяют допускаемые напряжения, об/мин;
− частота вращения того зубчатого колеса, по материалу которого определяют допускаемые напряжения, об/мин;
t – время работы передачи (ресурс) в часах; t = Lh.
|
|
|
Таблица 2.2
| Термообработка | Твердость зубьев** | Группа сталей | 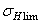 **, Па **, Па
| SH | 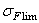 **, МПа **, МПа
| SF | 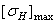 **, МПа **, МПа
| 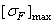 **, МПа **, МПа
| |
| на поверхности | в сердцевине | ||||||||
| Нормализация, улучшение | 180…350 НВ | 40, 45, 40Х, 40ХН, 45ХЦ, 35ХМ и др. | 2HB+70 | 1,1 | 1,8HB | 1,75 | 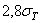
| 2,74HB | |
| Объемная закалка | 45…55 HRC | 40Х, 40ХН, 45ХЦ, 36 ХМ и др. | 18HRC +150 | 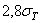
| |||||
Закалка ТВЧ по всему контуру (модуль 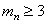 мм) мм)
| 56…63 HRC 45…55 HRC | 25…55 HRC | 55ПП, У6, 35ХМ, 40Х, 40ХН и др. | 17∙HRCпов +200 | 1,2 | 40HRCпов | |||
| Закалка ТВЧ по всему контуру (модуль mn < 3 мм) | 45…55 HRC | 35ХМ, 40Х, 40ХН и др. | 17HRCпов +200 | 40HRCпов | |||||
| Азотирование | 55…67 HRC 50…59 HRC | 24…40 HRC | 35ХЮМ, 38ХМЮА 40Х, 40ХФА 40ХНМА и др | 1,2 | 12HRCсердц +300 | 1,75 | 40HRCпов 30HRCпов | ||
| Цементация и закалка | 55…63 HRC | 30…45 HRC | Цементируемые стали | 23HRCпов | 40HRCпов | ||||
| Нитроцементация и закалка | 55…63 HRC | 30…45 HRC | Молибденовые стали 25ХГМ, 25ХГНМ Безмолибденовые стали 25ХГТ, 35Х | 23HRCпов | 1,5 | 40HRCпов | |||
| * Распространяется на все сечения зуба и часть тела зубчатого колеса под основанием впадины. ** Приведён диапазон значений твёрдости, в котором справедливы рекомендуемые зависимости для пределов выносливости и предельных допускаемых напряжений (рассчитывают по средним значениям твёрдости в пределах допускаемого отклонения, указанного в таблице); HRCпов − твёрдость поверхности, HRCсердц − твёрдость сердцевины. |
Постоянный режим нагрузки является наиболее тяжелым для передачи, поэтому его принимают за расчетный также в случае неопределенного (незадаваемого) режима нагружения.
Большинство режимов нагружения современных машин сводятся приближенно к шести типовым режимам (рис. 2.2):
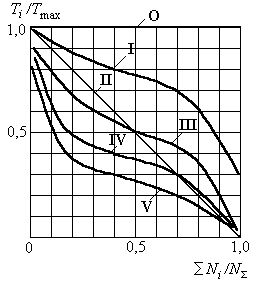
Рис. 2.2. 0 − постоянный, I − тяжелый, II − средний равновероятный, III − средний нормальный, IV − легкий, V − особо легкий
|
|
|
Режим работы передачи с переменной нагрузкой при расчете допускаемых контактных напряжений заменяют некоторым постоянным режимом, эквивалентным по усталостному воздействию. При этом в формулах расчетное число циклов NH перемены напряжений заменяют эквивалентным числом циклов NHE до разрушения при расчетном контактном напряжении.
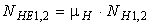 ,
,
где 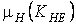 − коэффициент эквивалентности, значения которого для типовых режимов нагружения приведены в табл. 2.3.
− коэффициент эквивалентности, значения которого для типовых режимов нагружения приведены в табл. 2.3.
Таблица 2.3
| Режим работы | Расчёт на контакт. усталость | Расчёт на изгибную усталость | |||||||
| Термооб- работка | m /2 | 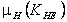
| Термическая обработка | m | 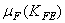
| Термическ. обработка | m | 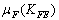
| |
| любая | 1,0 | улучшение, нормализация, азотирование | 1,0 | закалка объёмная, поверхност- ная, цементация | 1,0 | ||||
| I | 0,5 | 0,3 | 0,20 | ||||||
| II | 0,25 | 0,143 | 0,10 | ||||||
| III | 0,18 | 0,065 | 0,036 | ||||||
| IV | 0,125 | 0,038 | 0,016 | ||||||
| V | 0,063 | 0,013 | 0,004 |
Базовое число циклов NHG перемены напряжений, соответствующее пределу контактной выносливости 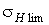 , рассчитывают по эмпирическим следующим зависимостям
, рассчитывают по эмпирическим следующим зависимостям
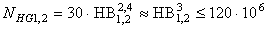 .
.
Из двух значений (для зубьев шестерни и колеса) рассчитанного допускаемого контактного напряжения в дальнейшем за расчетное принимают:
– для прямозубых (цилиндрических и конических) передач – меньшее из двух значений допускаемых напряжений 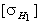 и
и 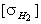 ;
;
– для косозубых цилиндрических передач с твердостью рабочих поверхностей зубьев Н 1 и 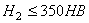 – меньшее из двух напряжений
– меньшее из двух напряжений 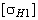 и
и 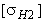 ;
;
– для косозубых цилиндрических передач, у которых зубья шестерни значительно (не менее 70...80 НВ) тверже зубьев колеса,
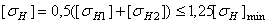 ,
,
где 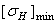 – меньшее из значений
– меньшее из значений 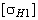 и
и 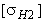 .
.
Допускаемые напряжения изгиба
Расчет зубьев на изгибную выносливость выполняют отдельно для зубьев шестерни и колеса, для которых вычисляют допускаемые напряжения изгиба по формуле
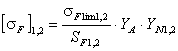 ,
,
где 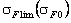 − предел выносливости зубьев по напряжениям изгиба, значения которого приведены в табл. 2.2;
− предел выносливости зубьев по напряжениям изгиба, значения которого приведены в табл. 2.2;
SF − коэффициент безопасности, рекомендуют SF = 1,5...1,75 (смотри табл. 2.2);
YA (КFC) − коэффициент, учитывающий влияние двустороннего приложения нагрузки (например, реверсивные передачи), при односторонней нагрузке YA = 1 и при реверсивной YA = 0,7...0,8 (здесь большие значения назначают при Н 1 и Н 2 > 350 НВ);
YN (KFL) − коэффициент долговечности, методика расчета которого аналогична расчету ZN (смотри выше).
|
|
|
При 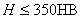
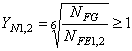 , но
, но 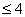 .
.
При Н > 350 НВ 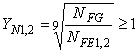 , но
, но 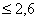 .
.
При 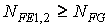 следует принимать
следует принимать 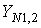 = 1. Рекомендуют принимать для всех сталей
= 1. Рекомендуют принимать для всех сталей 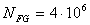 . При постоянном режиме нагружения передачи
. При постоянном режиме нагружения передачи
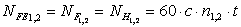 .
.
При переменных режимах нагрузки, подчиняющихся типовым режимам нагружения (рис. 2.2),
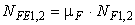 ,
,
где 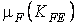 принимают по табл. 2.3.
принимают по табл. 2.3.
Вместо [a]f в формулу (9.14) подставляют меньшее из [a]fl и [a]f2.
Полученное значение модуля пг округляют в большую сторону по табл. 8.1. Рекомендуется модуль колес принимать минимальным. Уменьшение модуля зацепления пг и соответствующее увеличение числа зубьев ζ способствуют уменьшению удельного скольжения, что увеличивает надежность против заедания. При малом пг увеличиваются коэффициенты перекрытия εα (плавность зацепления) и к.п.д., уменьшаются шум и трудоемкость нарезания колес, заметно снижается отход металла в стружку.
С другой стороны, принимать m< 1 мм в силовых цилиндрических передачах не рекомендуется из-за опасности разрушения зуба при кратковременных перегрузках, а также из-за неоднородности материала и изнашиваемости.
2. Определяют число зубьев шестерни ζ ι и колеса ζ2. Для некорригированных прямозубых передач zlmin=17. Если Ζι< 17, то это означает, что для данной передачи более опасным являются изгибные, а не контактные напряжения. В этом случае передачу следует корригировать или принимать Ζι=17. Тогда z2=17w. Так как новое значение di = mz2 больше прежнего, то можно уменьшить b2 = b2 d2/d2.
Следует иметь в виду, что с увеличением z\ уменьшается шум, возрастает к.п.д., легче обеспечить точность зацепления. Рекомендуется z\ = 18...35.
3. Вычисляют фактическое передаточное число.
4. Определяют фактические основные геометрические размеры передачи. Делительные диаметры шестерни и колеса подсчитывают с точностью до 0,01 мм.
5. Проверяют пригодность заготовок колес. Чтобы получить при термообработке ранее принятые для расчета механические характеристики материалов шестерни и колеса, необходимо выполнить у с л о в и е пригодности их заготовок:
|
|
|
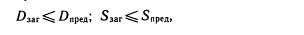
где £>пред и Япред — предельные размеры заготовок (см. табл. 8.4); Aiar и S3аг — размеры заготовок колес.
Для цилиндрической шестерни диаметр заготовки (см. рис. 8.26)

Здесь 6 мм — припуск на механическую обработку.
Для колеса с выемками (см. рис. 11.9) за толщину сечения заготовки принимают большую из двух значений:
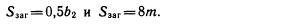
Для колеса без выемок — монолитного (см. рис. 11.8) 53аг = ^2 + 4 ММ.
Если условия пригодности заготовок не выполняются, то изменяют материал колес или вид термообработки.
6. Определяют окружную скорость колес υ и назначают степень точности изготовления (табл. 8.2).
50. Точность зубчатых колёс
Расчет зубчатых передач.
Из механических передач, применяемых в машиностроении, наибольшее распространение получили зубчатые, так как обладают рядом существенных преимуществ перед другими передачами.
Основные преимущества зубчатых передач:
• возможность осуществления передачи между параллельными, пересекающимися и скрещивающимися осями, иными словами при всех видах расположения осей;
• высокая нагрузочная способность и как следствие малые габариты;
• большая долговечность и надежность работы (ресурсы до 30 000 ч и более);
• высокий к.п.д. (до 0.97…0.98 в одной ступени);
• возможность применения в широком диапазоне скоростей (до 150 м/с), мощностей (до десятков тысяч кВт) и передаточных отношений (до нескольких сотен и даже тысяч);
• постоянство передаточного отношения.
В то же время для обеспечения надежной и качественной работы зубчатых передач к ним предъявляются повышенные требования к точности изготовления.
Многообразные условия применения зубчатых передач диктуют различные требования к их точности.
Для делительных и планетарных передач с несколькими сателлитами основным эксплуатационным показателем является высокая кинематическая точность, т.е. точная согласованность углов поворота ведущего и ведомого колес передачи. Кинематическая точность обеспечивается, например, при установке колеса на зубообрабатывающий станок с точной кинематической цепью с минимально возможным радиальным биением.
Для высокоскоростных передач (окружные скорости зубчатых колес могут достигать 60 м/с) основным эксплуатационным показателем является плавность работы передачи, т.е. отсутствие циклических погрешностей, многократно повторяющихся за оборот колеса. Циклическая точность обеспечивается, например, точностью червяка делительной передачи станка и точностью зуборезного инструмента. Плавность передачи значительно повышается после шевингования зубчатых колес или их притирки.
Для тяжелонагруженных тихоходных передач наибольшее значение имеет полнота контакта поверхностей зубьев. Контакт зубьев зависит от торцового биения заготовки и ряда других причин. Контакт зубьев значительно улучшается после притирки зубчатых колес.
|
|
|
Косозубые колёса


Косозубые колёса
Косозубые колёса являются усовершенствованным вариантом прямозубых. Их зубья располагаются под углом к оси вращения, а по форме образуют часть спирали.
- Достоинства:
- Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом.
- Площадь контакта увеличена по сравнению с прямозубой передачей, таким образом, предельный крутящий момент, передаваемый зубчатой парой, тоже больше.
- Недостатками косозубых колёс можно считать следующие факторы:
- При работе косозубого колеса возникает механическая сила, направленная вдоль оси, что вызывает необходимость применения для установки вала упорных подшипников;
- Увеличение площади трения зубьев (что вызывает дополнительные потери мощности на нагрев), которое компенсируется применением специальных смазок.
В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности
53. Цилиндрические косозубые и шевронные зубчатые передачи. Устройство и основные геометрические и силовые соотношения
Косозубые зубчатые передачи, как и прямозубые, предназначены для передачи вращательного момента между параллельными валамя (рис. 36). У косозубых колес оси зубьев располагаются не по образующей делительного цилиндра, а по винтовой линии, составляющей с образующей угол 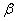 (рис. 37). Угол наклона зубьев р принимают равным
(рис. 37). Угол наклона зубьев р принимают равным 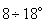 , он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.
, он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.
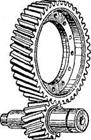
Рис. 36. Цилиндрическая косозубая передача
Передаточное число для одной пары колес может быть 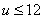 . В прямозубых передачах линия контакта параллельна оси, а в косозубых расположена по диагонали на поверхности зуба (контакт в прямозубых передачах осуществляется вдоль всей длины зуба, а в косозубых — сначала в точке увеличивается до прямой, «диагонально» захватывающей зуб, и постепенно уменьшается до точки).
. В прямозубых передачах линия контакта параллельна оси, а в косозубых расположена по диагонали на поверхности зуба (контакт в прямозубых передачах осуществляется вдоль всей длины зуба, а в косозубых — сначала в точке увеличивается до прямой, «диагонально» захватывающей зуб, и постепенно уменьшается до точки).
Достоинства косозубых передач по сравнению с прямозубыми: уменьшение шума при работе; меньшие габаритные размеры; высокая плавность зацепления; большая нагрузочная способность; значительно меньшие дополнительные динамические нагрузки.
За счет наклона зуба в зацеплении косозубой передачи появляется осевая сила.
Направление осевой силы зависит от направления вращения колеса (рис. 37), направления винтовой линии зуба, а также от того, каким является колесо — ведущим или ведомым. Осевая сила дополнительно нагружает валы и опоры, что является недостатком косозубых передач.
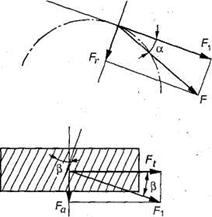
Рис. 37. Усилия в косозубой цилиндрической передаче
Шевронные зубчатые колеса представляют собой разновидность косозубых колес (рис. 38).
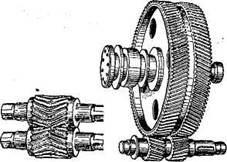
А) б)
Рис. 38. Шевронная зубчатая передача
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (рис. 38, а), называют шевронным колесом. Часть венца зубчатого колеса, в пределах которого линии зубьев имеют одно направление, называют полушевроном. Различают шевронные колеса с жестким углом (рис. 38, б), предназначенным для выхода режущего инструмента при нарезании зубьев. Шевронные передачи обладают всеми преимуществами косозубых, а осевые силы (рис. 39) противоположно направлены и на подшипник не передаются.
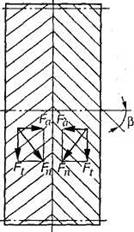
Рис.39. Усилия в зацеплении шевронных зубчатых колес
В этих передачах допускают большой угол наклона зубьев ( 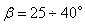 ). Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т.е. в тех случаях, когда требуется передавать большую мощность и высокую скорость, а осевые нагрузки нежелательны.
). Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т.е. в тех случаях, когда требуется передавать большую мощность и высокую скорость, а осевые нагрузки нежелательны.

Рис. 40
Косозубые и шевронные колеса в отличие от прямозубых имеют два шага и два модуля: в нормальном сечении (см. рис. 44) по делительной окружности — нормальный шаг рп, в торцовой плоскости — торцовый шаг рt. Из условия, что модуль зацепления равен шагу, деленному на число 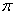 , имеем
, имеем 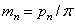 ;
; 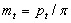 .
.
Для косозубых и шевронных колес значения нормального модуля тn стандартизованы, так как профиль косого зуба в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, т = тп (косозубые и шевронные колеса нарезают, тем же способом и инструментом, что и прямозубые). Нормальный модуль тп является исходным при геометрических расчетах.
Определим зависимость между нормальным и торцовым шагом и модулем через угол наклона зубьев.
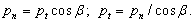
Если левую и правую части разделим на 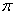 , получим
, получим
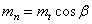 ;
; 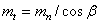 .
.
Геометрические параметры цилиндрической косозубой и шевронной передач с эвольвентным профилем зуба рассчитают по формулам, приведенным в табл. 15. По торцовому модулю тt рассчитывают делительные (начальные) диаметры, а до тп — все остальные размеры зубчатых колес.
Таблица 15. Геометрические параметры цилиндрической косозубой передачи
| Параметр, обозначение | Расчетные формулы | |
Нормальный модуль 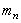
| 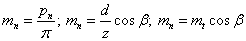
| |
Торцовый (окружной модуль) 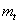
| 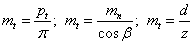
| |
Диаметр вершин зубьев в 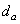
| 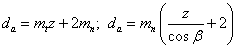
| |
| Делительный диаметр d | 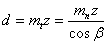
| |
Диаметр впадин зубьев 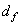
| 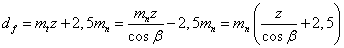
| |
Шаг нормальный 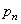
| 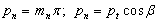
| |
Шаг торцовый (окружной) 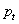
| 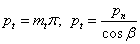
| |
Окружная толщина зубьев 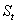
| 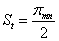
| |
Ширина впадин зубьев 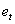
| 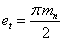
| |
Высота зуба 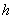
| 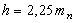
| |
Высота головки зуба 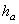
| 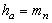
| |
Высота ножки зуба 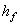
| 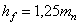
| |
Радиальный зазор 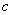
| 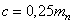
| |
Межосевое расстояние 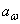
| 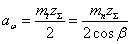
| |
Длина зуба 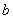
| 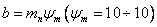
| |
Ширина венца 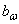
| 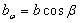
|
Окружная сила 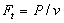 . На косой зуб действует осевая сила
. На косой зуб действует осевая сила 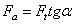 (см. рис. 37), радиальная (распорная) сила
(см. рис. 37), радиальная (распорная) сила 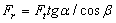 .
.
В косозубдй передаче сила 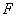 , действующая на зуб косозубого колеса (см. рис. 44), направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса, и составляет угол
, действующая на зуб косозубого колеса (см. рис. 44), направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса, и составляет угол 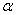 с касательной к
с касательной к
эллипсу.
Эту силу разложим на две составляющие: окружную силу на эквивалентном колесе 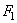 и радиальную (распорную) силу на этом колесе
и радиальную (распорную) силу на этом колесе 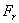 .
.
Если, в свою очередь, силу 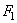 разложить по двум направлениям, то получим такие силы:
разложить по двум направлениям, то получим такие силы: 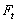 — окружную силу,
— окружную силу, 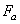 — осевую.
— осевую.
Для зубчатого колеса с шевронным зубом окружную силу 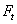 и распорную
и распорную 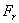 определяют по тем же формулам, что и для косозубой передачи т.е.
определяют по тем же формулам, что и для косозубой передачи т.е. 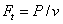 ,
, 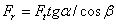 . В шевронной передаче осевая сила
. В шевронной передаче осевая сила  (см. рис. 39).
(см. рис. 39).
Винтовая передача (разновидность косозубой) состоит из двух косозубых цилиндрических колес (рис. 41). Однако в отличие от косозубых цилиндрических передач с параллельными валами касания между зубьями здесь происходит в точке и при значительных скоростях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.
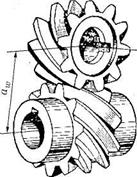
Рис.41. Винтовая зубчатая передача
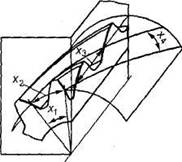
Рис. 42
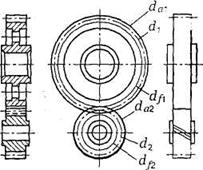
Рис. 43
Модуль зубчатого колеса
Модуль зубчатого колеса
геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности d д к числу зубьев z или отношению шага t по делительной окружности к числу: m = d д /z = ts /π. Для косозубых цилиндрических колёс различают: окружной модуль ms = d д /z = ts /π, нормальный модуль mn = tn /π, осевой модуль ma = tа /π, где ts, tn и ta — соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к. стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача).
54-56
http://www.cross-kpk.ru/ims/02708/OTM/Glava5/razdel6/razdel56.html
|
|
|


