 |
Свойства ф-ции распред(ФР).
|
|
|
|
1. Если СВ непрерыв, то и ФР явл-ся непрерыв.
2. Если Х2>Х1, то F(X2)>F(X1), т.е. ФР явл-ся неубывающей.
3. Если 0<р(А)<1, то 0<р(θ≤Х1)=F(X1)<1.
Она может быть представлена графически (рис1)
Рассм-м СВ в небольшом проиежутке: Х≤θ<(Х+ΔХ);р(Х≤θ<Х+ΔХ)=F(Х+ΔХ)-F(X)(рис2)
α – наклон секущей в точках рез-та Х, Х+ΔХ; 
;
- плотность распред.
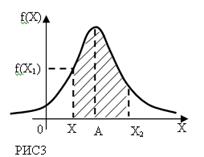
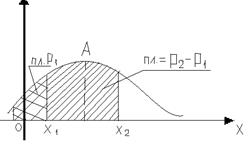
Плотность распр хар-т закон распр. Р (рис3). А – точка перегиба.
В соотв. с формулой Ньютона-Лейбница 
(*) хар-т площадь (заштрихованную) ограниченную кривой плотности распр и ординатами в точках доп знач Х1 и Х2. 
F(+∞)=р(θ≤+∞)=1; F(–∞)=р(θ≤–∞)=0;
Т.е. площадь под кривой распред равна 1.
105. Координаты центра распределения, мода, медиана, моменты распределения СВ
1) Координаты центра распределения
Предположим, мы имеем СВ с характеристиками 
- допустимые значения и вероятности появления данных допустимых значений 
, т.е. имеем функцию распределения.
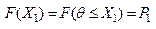
Координаты центра распределения имеет вид:
Если рассмотреть допуст-е значения как координаты точек, расположенных вдоль некоторого стержня, а вероятности данных допустимых значений как массы грузов, подвешенных в этих точках, то координаты центра распределения будет совпадать с центром тяжести образовавшейся системы, поэтому ее называют средним взвешенным звеном или математическим ожиданием М(
).
2)Мода (М0)
Это значение С.В. при максимальном значении плотности распределения.
X=M0, при f(X)=fmax(X)
3) Медиана (Ме)
- это значение СВ, ордината в точке которой делит площадь под кривой плотности распределения пополам.
P(θ≤Me) = P(θ≥Me)
Попадание СВ слева и справа от медианы равновероятно
P(θ≤Me) = P(θ≥Me) = 0,5
|
|
|
При симметричном распределении мода, медиана и математическое ожидание совпадают: M0 = Me = M(θ).
4)Моменты распределения
Моменты распределения бывают начальные и центральные.
Начальные моменты характеризуют распределения неисправленных результатов.
-начальный момент
Центральные моменты распределения характеризуют распределение исправленных результатов, в которых M(X)=0.
Центральный момент S-порядка имеет вид:
т.к. 
,то получим
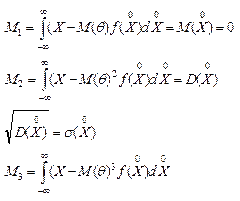
M3 –характеризует ассиметрию распределения
- коэффициент ассиметрии
-характеризует островершинность и плосковершинность распределения. Его характеристикой является эксцесс.
ε=ЕХ =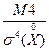 
В ряде случаев ε бывает очень большим, поэтому в место ε вводится контрэксцесс
- контрэксцесс
106. Аксиомы теории вероятности
При измерениях ФВ устан-ся причинно-следственные связи м/у отдельными явлениями: явл-причина (фактор), явл-следствие (результат). Явл-следствие разбивается на частные явления относит-но которых нужно выяснить произошли они или не произошли. Такие частные явления наз. событиями.События, которые при заданном комплексе факторов (явл-причин) обязат-но произойдет наз. достоверным, кот. не произойдет- невозможным. А кот-ое либо произойдет, либо нет – случайным. Возможность случайного события ( сс) становиться достоверным хар-ся вер-тью. Результат измерения по выяснению характера соб-я(достоверное или невозмо-жное) наз. исходом. Вер-ть сс равна отношению числа исходов благо-приятствующих соб-ю к числу всех возможных исходов.
р-вероятность, А – сс, р(А) – вер-ть сс А;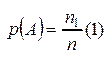 
; 
n1- число исходов благоприят-х соб-ю, n-число всех возможных исходов.
Аксиомы теории вер.
1. Вер любого соб. число неотр-ное, р(А)≥0.
2. Вер достоверного соб. равна 1, р(А)=1.
3. Вер невозможного соб. равна 0, р(А)=0.
4. Вер сс: 0<р(А)<1.
5. Совместная вер противопол.-х соб равна 1: р(А+Ā)=р(А)+р(Ā)=1.
|
|
|
107. Закон распределения непрерывных СВ.Закон нормального распределения
Для этого необходимо знать закон распределения СВ,т.е функцию и плотность распределения
(1)плотность нормального распределения
F(x)= 
(2)Функция нормального распределения
-среднее квадратичное отклонение
функция распределения с а=0,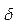 
=1 называется стандартом нормального распределения
переход от нормального к стандартному можно представить графически
Свойства нормального распределения. 
108. Равномерный закон распределения случайных величин
Равномерный закон распределения (Закон равной плотности).
Если непрерыв случ велич X приним знач-я лишь в пределах некот конечного инт-ла а 
X 
b c постоян плотностью распр-ия f(x)=c=const, то такой з-н распр-ия наз-ся равномерным.
Определим знач-е константы С, исходя из св-ва плотности вер-ти:
=> C= 1/(b-a)
Ф-ция распр-ния случ вел X, распред-ной по равном-му з-ну:
Ее мат ожидание:
M(X)= 
xf(x)dx=(b2-a2)/(2(b-a))=(b+a)/2]
Ее дисперсия:
D(X)= 
[x- M(X)]2f(x)dx=1/(b-a) 
[x- (b+a)/2]2dx=(b-a)2/12
109. Внесистемные единицы ФВ
1. Кратные и дольные
Системные единицы могут быть очень большими или очень маленькими, поэтому пользуются кратными и дольными единицами.
x = {x}[x]
k – коэффициент пересчета
l = 2 км = 2000 м
х1 = 2 км
х2 = 2000 м
{x1}/{x2} = [x2]/[x1] = k = 10n
множитель приставка
Кратной называют единицу, в целое число раз большую системной или внесистемной единицы.
Дольной называют единицу, в целое число раз меньшую системной или внесистемной единицы.
2000 / 2 = км / м = k
k = 103, кило
2. Относительные и логарифмические
Относительная величина представляет собой безразмерное отношение ФВ к ФВ, принятой за исходную.
{x1}/{x0} = k
x0 – исходная величина
Относительные величины могут выражаться в безразличных единицах (k = 1·100), в процентах (k = 1·10-2), в промилях (k = 1·10-3), в миллионных долях (ppm, k = 1·10-6).
Логарифмическая величина представляет собой логарифм десятичный, натуральный или при основании 2 безразмерного отношения двух одноименных ФВ.
Бел (Б)
1) 1Б = lg (N1/N2), где N1 = 10·N2
N1 и N2 – одноименные энергетические величины
|
|
|
