Вывод уравнения геотермограммы

Акустический каротаж

 

Акустический каротаж (АК) основан на изучении полей упругих волн в скважинах и заключается в измерении скорости распространения упругих волн ультразвуковой (УЗ) частоты и их затухания.

Как известно, скорость распространения упругих волн в различных горных породах не одинакова. Для примера в табл. 16.2 приведены скорости продольных волн в различных средах.

Таблица 16.2. Скорость распространения продольных волн в различных средах

 

Среда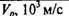
Глина	1,2-2,5
Песчаник плотный	З-6
Известняк	3-7,1
Каменная соль	4,5-5,5
Кристаллические породы	4,5-6,5
Цемент	3,5
Сталь	5,2
Воздух	0,33
Нефть	1,3-1,4
Вода	1,5
Буровой раствор	1,5-1,7

Для АК обычно используются так называемые "трехэлементные" зонды, содержащие два излучателя и один приемник упругих волн или, наоборот, два приемника и один излучатель. Излучатели, как правило, магнитострикционного типа, приемники - пьезоэлектрического.

Работу аппаратуры АК рассмотрим на примере зонда с двумя излучателями и одним приемником ГЩИг (рис. 16.10).

Излучатели периодически посылают пакеты из 3-4 периодов УЗ колебаний с частотой 10-75 кГц с колоколообразной формой огибающей. Частота посылки самих пакетов— 12,5-25,0 Гц.

Упругие импульсы от источников, пройдя через буровой раствор, возбуждают колебания в стенках скважины. Упругие колебания, попадающие на стенку скважины под углом полного внутреннего отражения, возбуждают в ней скользящую преломленную волну, которая, распространяясь со скоростью, присущей данной горной породе, достигает приемника.

Путь волны от источника Hi до приемника П составит И1O1ОП, а время пробега . Путь волны от источника И₂ –И₂О₂О₁П, время пробега - . Интервал времени между первыми вступлениями волны от первого и второго источников Δτ составит .

Как следует из рис. 16.10, расстояние О2О1 равно расстоянию между обоими источниками ЛЬ, называемому базой зонда. За точку записи принимают середину базы. Отсюда скорость распространения упругих волн: (16.3)

Обратное отношение 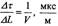называется интервальным временем. Амплитуды колебаний от обоих источников одинаковы, поэтому отношение амплитуд А1 и А2,
зарегистрированных приемником, характеризует затухание упругих волн на участке ΔL. Коэффициент затухания

Затухание упругих волн зависит от состава горных пород, пористости и состава флюида в порах (в газе затухание больше, чем в жидкости), а скорость их распространения - от состава и пористости.

Связь между пористостью К„ и скоростью распространения oписывается так называемым "уравнением среднего времени": (16.5)

где Vж- скорость упругих волн в жидкости, заполняющей поры породы; Vск- скорость упругих волн в минеральном скелете.

 

Уж и VCK определяют по результатам лабораторных измерений или берут из справочников; V— определяют по данным АК. Из этого уравнения можно найти пористость:

Кроме пористости и характера насыщения, по АК может быть определено положение контактов и мощность пластов, отличающихся по своим акустическим свойствам.

Для пластов большой мощности (h>ΔL) она определяется по правилу полумаксимума, для тонких - мощность, найденная по правилу полумаксимума, больше истинной на размер базы зонда. В обоих случаях при равенстве акустических свойств подстилающих и перекрывающих пород аномалии V симметричны относительно середины пласта, но в первом случае Vmax = Vm, а во втором Vmax < Vm (рис. 16.11, а и б).

 

 

 

 

Рис. 16.11. Кривые акустического каротажа над пластами большой и малой мощности, отличающимися повышенной скоростью распространения упругих волн

Область применения метода АК - главным образом, месторождения нефти и газа, в последнее время метод начинает применяться и на рудных, и на угольных месторождениях.

 

Решаемые задачи: литологическое расчленение разрезов, определение пористости и характера насыщения пор, определение положения водонефтяного контакта (ВНК) и газо-жидкостных контактов (ГЖК), цементометрия скважин; на рудных месторождениях - изучение геолого-технических условий.

Кроме ультразвукового метода, описанного выше, при исследовании скважин находят применение низкочастотный широкополосный акустический метод (НШАМ), в котором изучается акустическое поле в диапазоне частот от 5 до 20 кГц; интегральный акустический метод и вертикальное сейсмическое профилирование (ВСП), при которых источник колебаний устанавливается на поверхности, а приемники в скважине; метод акустического прозвучивания (МАП), при котором источник и приемник упругих волн устанавливаются в разных скважинах, и некоторые др.

 

Термометрия скважин

Термометрия занимается изучением естественных и искусственных тепловых полей в скважинах и окружающих их горных породах.

Естественные поля могут быть связаны с региональным (глубинным) тепловым полем Земли, а могут быть обусловлены и местными процессами, например, окислением сульфидных руд, радиоактивным распадом, растворением солей, притоком подземных вод или выделением газа в скважину.

Искусственные поля могут возникнуть под действием тепла бурового раствора, схватывающегося цементного камня или специальных скважинных нагревателей. Подробно все причины возникновения тепловых полей в скважинах перечислены на рис. 15.1.

Температурные измерения могут проводиться в установившемся или неустановившемся тепловом режиме скважины. При установившемся режиме температура бурового раствора не отличается от температуры стенок скважины, т.е. теплообмен между ними уже закончен.

При неустановившемся режиме происходит теплообмен между буровым раствором и горной породой. Разность температур между ними определяется по формуле:

где ∆t₀ - разность температур в начальный момент времени т = 0;

d - диаметр скважины;

а - коэффициент температуропроводности (о нем дальше).

Расчеты показывают, что для установления стационарного режима с точностью до 5% необходима экспозиция около 100 суток (при диаметре скважины 20 см).

Физические основы метода

Согласно теории, распространение теплового поля в среде описывается дифференциальным уравнением теплопроводности (уравнение Фурье), которое для однородной изотропной среды имеет вид:

Величина, обратная λ, называется удельным тепловым сопротивлением

Интегрирование этого уравнения в условиях неустановившихся тепловых процессов, когда ∂t/∂τ≠0, представляет собой сложную задачу, решаемую лишь для наиболее простых случаев.

При установившемся процессе теплообмена ∂t/∂τ= 0 это уравнение обращается в уравнение Лапласа: V²t=0, т.е. распределение теплового поля описывается тем же законом, что и стационарное электрическое поле или гравитационное поле в пространстве, где нет дополнительных масс.

Проследим аналогию установившихся тепловых и электрических полей более подробно (табл. 15.1).

Из приведенной аналогии видно, что удельное тепловое сопротивление ξ играет такую же важную роль для тепловых полей, как и удельное электрическое сопротивление р для электрических. Значения ξ для различных горных пород приведены в табл. 15.2.

Таблица 15.2. Коэффициент теплопроводности и удельное тепловое сопротивление горных пород (по Г.А. Череменскому, 1972)

№ п/п	Горная порода, вещество	Коэффициент теплопроводности	Удельное тепловое сопротивление
1.	Гранит	2,3-4,1	0,24-4,3
2.	Габбро	1,7-2,9	0,34-5,9
3.	Дунит	3,1-5,0	0,20-5,0
4.	Глина	0,17-1,7	0,58-5,8
5.	Песок	0,35-3,5	0,29-2,9
6.	Песчаник	0,7-5,8	0,17-1,43
7.	Известняк	0,8-4,1	0,24-1,25
8.	Каменная соль	6,2	0,16
9.	Вода	0,6	1,67
10.	Нефть	0,14	7,15
11.	Воздух	0,024	41,6

Таким образом, удельное сопротивление различных горных пород различается больше, чем на порядок. Его величина сильно зависит от пористости и влажности пород. (Последним фактором объясняется большой диапазон изменения теплового сопротивления осадочных пород).

По данным новейших исследований тепловых свойств, проведенных методом оптического сканирования (Ю. Попов и др., 2001), тепловое сопротивление горных пород очень изменчиво и в пределах интервала в 5-10 м, а иногда и участка керна длиной 7-20 см, может изменяться на 70-100%. Так же, как и электрическое сопротивление, тепловое сопротивление одних и тех же горных пород может различаться в зависимости от направления, в котором оно измеряется. Наиболее велика анизотропия тепловых свойств у слоистых горных пород. Разница в теплопроводности по слоистости и поперек нее может достигать 2,0-2,5 раз

 

 

Вывод уравнения геотермограммы

Вывод этого уравнения дается по проф. А.К. Козырину.

Рассмотрим решение уравнения Лапласа для случая установившегося теплообмена между двумя полупространствами, одно из которых имеет постоянную температуру. Такой процесс наблюдается, например, в породах, перекрывающих магму, при условии их горизонтального залегания и отсутствия дополнительных источников тепла (рис. 15.2).

 

 

Начало координат расположим в пределах так называемого "нейт­рального слоя", в котором сезонные и суточные колебания температуры не превышают точности измерений, а величина последней равна среднегодовой темпера­туре t0 данной местности. Оси х и у расположим в плоскости нейтрального слоя, а ось z направим вертикально вниз. Таким образом, распределение теплового поля не будет зависеть от координат х и у, следовательно, будет иметь осевую сим­метрию, а уравнение Лапласа упростится до выражения 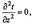следовательно и где с1 и с2- постоянные, значение которых нужно определить. Поскольку , а в нашей задаче температура растет в направлении оси z, можно полагать, что с1=Г. В плоскости нейтрального слоя, при , следовательно, c2=t0, и решением задачи будет выражение:

 

Рис. 15.2. К выводу уравнения геотермограммы

Однако это решение было бы справедливым, если бы тепловые свойства всех слоев, перекрывающих магму, были одинаковы. Но они разные. Поэтому общее решение будет иметь вид:

где ,- мощность i-го слоя

Это уравнение линии, которая называется

ломаной геотермограммой. Уравнение одного, i-го звена геотермограммы:

откуда: Это величина маленькая, поэтому на практике оперируют с более крупной величиной 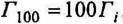которая называется геотермическим градиентом.

Среднее для всей Земли значение (15.7), хотя в разных местах значения 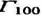варьируют от 0,2 до 20 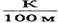. Используют также обратную величину - геотермическую ступень

(15.8)

 

Измерение геотермического градиента и изучение геотермограмм составляет предмет геотермии или метода естественного теплового поля Земли.

Необходимым условием получения геотермограмм в скважинах является наличие установившегося теплообмена (q = const) между скважиной и окружающими породами, т.е. равенство температур бурового раствора и горных пород.

В плоскости геологических разрезов результаты геотермических исследований изображаются в виде геотермограмм скважин t = f(H), которые представляют собой ломаные линии с точками перелома напротив границ пластов с разными тепловыми сопротивлениями (рис. 15.3). Эти графики могут быть пересчитаны в диаграммы температурного градиента или теплового сопротивления по закону Ома в дифференциальной форме, т.к. q = const, то 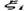пропорционально Гi

Строят также профили геоизотерм (рис. 15.4).

 

В плане результаты геотермических исследований изображают в виде планов и карт изотермических поверхностей (t=const) или карт рельефа геоизотерм (H=const), которые выглядят так, как показано на рис. 15.5, а и б.

Рис. 15.5. Карта геоизотерм (а) и карта рельефа геоизотермы t=30" (б)

 

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: