Глава 7.Экспериментальные методы исследования процессов ОМД

Общие положения. При разработке технологических процессов обработки металлов давлением и проектировании оборудования большое значение имеют экспериментальные методы определения усилий и деформаций, которые проводятся в лабораторных условиях, т. к. проведение эксперимента в производственных условиях затруднено техническими и организационными причинами, а исследование деформаций и напряжений в большинстве случаев невозможно. Результаты лабораторных исследований могут быть обобщены, если условия проведения на лабораторном оборудовании подобны производственным, при этом должны соблюдаться законы подобия.

Для правильной оценки надежности работы действующих технологий и оборудования по производству проката, труб, поковок, и др. видов обработки, а также совершенствования и проектирования новых процессов применяют физическое или математическое моделирование []. Для исследования напряженно-деформированного состояния металла при пластическом формоизменении широко применяют экспериментальные и экспериментально-теоретические (расчетные) методы, которые позволяют изучить отдельные параметры исследуемых процессов. При этом важно, чтобы результаты, полученные на модели соответствовали реальному процессу, необходимо соблюдения основным принципам теории подобия и физического моделирования [1].

Усилия, напряжения и деформации при обработке давлени­ем в ряде случаев могут быть определены экспериментально в производственных условиях при изготовлении изделий и полу­фабрикатов на промышленных агрегатах. Однако постановка этих экспериментов часто сопряжена с большими затратами ма­териалов и простоями оборудования.

Некоторые вопросы экспериментально вообще невозможно изучить в производственных условиях, например, распределение напряжений по объему тела. При разработке принципиально новых технологических процессов обработки давлением также невозможна постановка экспериментов в производственных условиях.

Поэтому обычно тот или иной вопрос предварительно экспе­риментально исследуется в лабораторных условиях на образ­цах, (моделях) в широком диапазоне изменения различных фак­торов. Полученные в лабораторных условиях данные пересчитывают с модели на натуру. Затем в производственных условиях проводят поверочные эксперименты в ограниченном числе. Такой путь экспериментального исследования применяют не только при определении усилий, напряжений н формоизменения, но и при исследовании влияния условий деформации на измене­ние свойств и структуры металла. Последнее особенно важно при разработке технологических процессов обработки давлением новых сплавов.

Эксперименты в лабораторных условиях проводят обычно на установках меньшей мощности и с образцами меньших размеров по сравнению с размерами натурных.

Для того чтобы закономерности и количественные данные, полученные в лабораторных условиях, можно было бы распро­странить на производственные условия, необходимо соблюдать подобие обоих процессов.

7.1. Основы теории подобия и физического моделирования процессов ОМД.

В. Л. Кирпичев в 1874 г. сформулировал закон подобия для упругой деформации металлов. Согласно этому закону, работы деформации геометрически подобных тел, изготовленных из одного и того же материала, пропорциональны объемам, а уси­лия — сходственным площадям; при этом удельные усилия равны.

Ф. Кик в 1879 г. предложил распространить этот закон и на пластическую деформацию. Однако в условиях пластической де­формации, особенно при высоких температурах, закон подобия Кирпичева — Кика нельзя применить безоговорочно из-за невоз­можности обеспечения полного подобия процессов. Согласно за­кону подобия деформируемые тела должны быть геометрически подобны и физически одинаковы [6].

Геометрическое подобие будет соблюдено, если отношения сходственных линейных размеров: длины l, ширины b, высоты h модели (с индексом «м») и натуры (с индексом «н») будут оди­наковы, т. е.

(7.1)

где п — масштаб моделирования или коэффициент подобия.

Отношения сходственных площадей будут пропорциональны квадрату масштаба моделирования, а отношения объемов — кубу.

Для соблюдения геометрического подобия в процессе дефор­мации необходимо, чтобы степени деформации модели и натуры были равны: ε_Н = ε_М.

Инструменты для деформирования модели и натуры должны быть также геометрически подобны и отношение их линейных размеров должно быть равно масштабу моделирования.

Геометрическое подобие при пластической деформации осу­ществить легко.

Для соблюдения условий физического подобия необходимо, чтобы физические свойства модели и натуры: химический состав, фазовое состояние, микро- и макроструктура в исходном со­стоянии и в каждый момент деформации были одинаковые. Кро­ме этого, должны быть одинаковы температурный режим и условия трения на кон­тактных поверхностях. При упругой деформации свойства металла не изменяются. Трением на контактной поверхности из-за малой величины деформации можно пренебречь. Поэтому если обеспечить одинаковые свойства модели и натуры в исход­ном состоянии, то они будут одинаковы и в процессе деформа­ции. Следовательно, при упругой деформации легко обеспечить и физическое подобие модели и натуры.

При пластической деформации обеспечить одинаковые физи­ческие свойства модели и натуры (особенно в интервале темпе­ратур фазовых превращений) невозможно. Объясняется это тем, что отношение скоростей v и продолжительности деформирования, а следовательно, и скоростей деформации ζ модели и натуры дол­жно быть различным для обеспечения одинаковой температуры, одинаковых условий трения и условий протекания процессов упрочнения и разупрочнения. Для обеспечения одинаковой температуры модели и натуры в процессе деформации при одинаковой исходной необходимо скорость деформирования v модели увеличить в п раз, так как мо­дель охлаждается быстрее вследствие большего в п раз отноше­ния поверхности к объему. Следовательно, для соблюдения теп­лового подобия (равенства температур) необходимо, чтобы v _м = nv _н. Тогда

отношение скоростей деформации ζмодели и натуры будет равно квадрату масштаба моделирования: . Продолжительность деформирования модели t _м должна быть в п² раз меньше продолжительности деформирования натуры: t _м=

Для соблюдения одинаковых условий трения, помимо одинако­вых материалов инструмента, качества обработки его поверхно­сти, смазки и температуры, необходимо обеспечить одинаковую скорость скольжения металла по инструменту, что воз­можно только при одинаковых скоростях деформирования моде­ли и натуры: v _м = v _н, а скорость деформации модели должна быть в п раз больше скорости деформации натуры: ζ_м = n ζ_н

Продолжительность деформации модели t _м = t _н/ n.

Для соблюдения одинаковых условий протекания процессов упрочнения и разупрочнения при одинаковых степенях деформа­ции, необходима одинаковая скорость деформации: ζ_м = ζ_н. Тогда скорость деформирования модели должна быть в п раз меньше скорости деформирования натуры: ζ_м = ζ_н/ n, а продолжительность деформирования натуры и модели долж­на быть одинакова: t _м = t _н.

Таким образом, как отмечает Н.П.Громов [3], для обеспе­чения теплового подобия по условиям трения и по условиям упрочнения и разупрочнения необходимо различное отношение скоростей деформирования модели и натуры. Следовательно, единый скоростной критерий подобия при горячей обработке металлов давлением отсутствует.

При холодной обработке давлением ввиду незначительного изменения температуры металла из-за выхода тепла и незначи­тельного влияния скорости деформации на сопротивление дефор­мации моделирование осуществляется с достаточной для прак­тики точностью.

Необходимость лабораторных исследований процессов горя­чей обработки металлов давлением привела к разработке методов приближенного моделирования этих процессов. Так, Ю. М. Чижиков [4] при моделировании процессов горячей прокатки применяет «коэффициенты несоответствия», характери­зующие отличия действительных условий эксперимента от усло­вий подобия. Значения коэффициентов несоответствия могут быть определены опытным путем.

В работе [5] авторами дан подробный обзор принципов моделирования процессов ОМД.

7.2. Экспериментальные методы исследованияконтактных напряжений.

В практике получили распространение следующие экспериментальные методы исследования напряжений: штифтов, разрезных силоизмерительных устройств и поляризацонно- оптический.

Метод точечных месдоз (штифтовый метод). Методика экспериментального исследования распределения удельного давления по дуге контакта прокатываемой полосы с валками впервые была предложена А.Ф.Родзевичем-Белевичем еще в 1913 г. В валке просверливают отверстие – осевое и радиальное. В радиальном отверстии хорошо отшлифованный поршень, выходящий на поверхность контакта с полосой. Отверстие заполняется жидкостью и давление прокатки через поршень передается на жидкость и измеряется манометром.

Результаты измерения распределения давлений по дуге захвата при прокатке впервые были опубликованы В.Луегом в 1933 г.

Экспериментальные исследования нормальных напряжений при продольной прокатке проводились также А. А. Королевым, Н. И. Сведе-Швец, В. П. Северденко, А. Н. Гришковым, А. П. Чекмаревым, П. Л. Клименко и другими исследователями; при осадке – Е.П.Унксовым, Н.И.Мицкевичем и др. [10-12 и др.], а измерение нормального давления при винтовой прокатке данным методом впервые было проведено И.Т.Жердевым [13], позднее В.Я.Осадчим и А.З.Глейбергом [14]. На рис.7.1 показана одна из конструкций точечной месдозы. Рабочая часть месдозы – тонкостенный цилиндрический стакан 2 - является упругим элементом и выполняется из инструментальной стали или цветных металлов, например, бронзы, толщиной 0,2 мм. Продольная деформация цилиндра, возникающая от действия усилия металла на штифт, измеряется проволочными датчиками (рабочими), которые наклеивают вдоль рабочей поверхности и соединяются в одно плечо полумоста, а второе плечо состоит из компенсационных датчиков, которые наклеивают на

цилиндрическую недеформируемую часть цилиндра. Штифт опирается на дно тонкостенного цилиндрического стакана и постоянно прижимается к нему пружиной, которая удерживает его от выступания из канала деформирующего инструмента. Месдоза со штифтом при помощи резьбы ввинчивается в тело сегмента деформирующего инструмента и закрепляется контргайкой. Торец штифта выводится на контактную поверхность инструмента (валка, оправки, матрицы). При обработке давлением силовое воздействие месдозы воспринимается штифтом и передается цилиндрической части и преобразуется в электрический сигнал, который регистрируется измерительной аппаратурой.

 

Рис. 7.1 Общий вид точечной месдозы (размеры даны в мм): 1 – штифт; 2 – стакан; 3 – пружина; 4 – контргайка; 5 – валок [12]	Рис. 7.2 Общий вид универсальной точечной месдозы

 

 

Конструкции точечных месдоз (см. рис.7.1 и 7.2) надежны в эксплуатации и отличаются малыми габаритами, что позволяет размещать их на очень малых расстояниях друг от друга.

Дальнейшим развитием в исследовании контактных напряжений при ОМД явилась разработка на кафедре ОМД Уральского Государственного университета конструкции универсальной точечной месдозы, которая позволяет измерять величину и направление полного напряжения на малой площадке контактной поверхности деформирующего инструмента при прокатке, ковке, штамповке, волочении, прессовании [1,10]. Принцип действия данного метода заключается в том, что действующая на штифт равнодействующая сила Р раскладывается на три взаимно перпендикулярные составляющие: Р_Z (ориентирована перпендикулярно контактной поверхности и показывает нормальное давление на поверхность штифта); две другие оставляющие Р_х и Р_Y являются проекциями сил трения, возникающие на этой поверхности. Для регистрации осевой составляющей Р_Z на наружной поверхности полой месдозы в направлении его оси наклеены два рабочих датчика D_Z и H_Z (рис.7.2), которые соединены последовательно и включены в одно плечо мостовой схемы. Два компенсационных датчика В_k и F_k этого моста наклеены на поверхность стаканчика так, что они тоько контактируют с ней, но не деформируются при упругой деформации стаканчика-месдозы. Для регистрации составляющих Р_x и Р_y, действующих в плоскости, перпендикулярной оси штифта месдозы, на поверхность стканчика месдозы наклеены еще четыре датчика A_x; E_x и C_y; G_y, так, что плоскости, проходящие через ось штифта и середины диаметрально противоположных датчиков, взаимно перпендикулярны. Диаметрально противоположные датчики каждой пары включены в смежные плечи моста так, что деформация растяжения одного и сжатия другого вызывают разбаланс одного знака. Оба датчика одновременно являются и рабочими и компенсационными. Отличительной особенностью конструкции универсальной точечной месдозы заключается в том, что ее рабочая часть выполнена воедино со штифтом, что позволяет соблюсти соосность диаметра штифта и диаметра рабочей части месдозы и устранить внецентренную нагрузку на ее рабочую часть.

На рис. 7.3 показаны конструкции валка, линейки и оправки с расположенными универсальными точечными месдозами, разработанные В. Я. Осадчим и А. П. Коликовым с сотрудниками [15,16]

Рис.7.3. Схема размещения точечных месдоз в валке, оправке и линейке в стане винтовой прокатки [15]: 1 – валок; 2 - точечные месдозы; 3 – линейка; 4 – оправка.

Можно считать, что в настоящее время штифтовый метод экспериментального определения нормальных исследований достаточно хорошо освоен.

Метод разрезных силоизмерительных устройств разработан И.М.Павловым с сотрудниками и впервые применен для исследования интегральных контактных напряжений при продольной прокатке [17]. Метод основан на принципе использования разрезного инструмента, например, валка и позволяет определять интегральные касательные Т(х) и нормальные Р(y) усилия при пластической деформации в реальных условиях обработки давлением. Дифференцирование экспериментальных кривых Т(х) и Р(y) позволяет получать эпюры нормальных р(y) и касательных τ(х) напряжений.

На рис.7.4 представлены конструкции разрезных силоизмерительных устройств: валкового торсиометра и силоизмерительной линейки, разработанных В. Я. Осадчим и А. П. Коликовым с сотрудниками в МИСиС для исследования процесса винтовой прокатки сплошных заготовок в полые гильзы [18]. Конструкция валкового торсиометра (рис.7.4,а) представляет собой валок 2, в сплошное тело которого врезан сегмент 4, имеющий подвижную планку 5. Планка расположена на шариковых опорах 6, что обеспечивает минимальные потери на трение, и опирается на две месдозы 6 для измерения нормального давления. В сегменте по обе стороны планки установлены четыре месдозы 8 (по две с каждой стороны) для измерения тангенциального усилия на валок. Усилие, действующее на валок в осевом направлении, измеряется месдозой 7. На рис. 7.4,б представлена конструкция силоизмерительной линейки, рабочей частью которой является подвижная планка 1, опирающаяся через шариковые опоры на основание линейки 2. Перемещение линейки в боковом направлении ограничено двумя тензометрическими болтами 4, которые фиксируют тангенциальное усилие на линейку; осевое усилие на линейку фиксируется месдозой 4. Измерение нормального усилия металла на линейку производится двумя цилиндрическими месдозами, расположенными под линейкодержателем.

Рис.7.4. Разрезные силоизмерительные устройства стана винтовой прокатки: а – валковый торсиометр; б – силоизмерительная линейка (описание в тексте).

 

Однако как отмечено в работе [1] тензометрические методы позволяют исследовать

напряженное состояние только на контакте металла с инструментом. Одной из труднейших задач остается экспериментальное определение напряженного состояния в объеме деформируемого тела. Частично решает эту проблему оптический метод.

Поляризационно-оптический метод (метод фотоупругости) основан на использовании различных оптических явлений в некоторых прозрачных материалах, которые выбираются в качестве модели исследуемого материала. При просвечивании таких материалов поляризационным светом возникают оптические явления, которые позволяют связать наблюдаемую картину с механическим состоянием тела, т.е. определить упругие контактные напряжения в инструменте из прозрачного оптически активного материала. В качестве оптических чуствительных материалов моделей применяют материалы на основе органического стекла, эпоксидных смол, поликарбоната и др. Распределение напряжений на контактной поверхности инструмента соответствует распределению напряжений на контактной поверхности деформируемого тела.

На рис.7.5 приведена принципиальная схема прибора (полярископа) для исследования напряженного и деформированного состояний деформируемого тела данным методом.

 

Рис.7.5. Принципиальная схема полярископа: 1 – источник света; 2 – поляроид; 3 – модель в виде пластины из прозрачного материала, нагруженная по периметру; 4 – второй поляроид или анализатор.

Изображение просвечиваемой модели проецируется на экран. Обычно плоскости поляроидов 2 и 4 скрещены, т. к. располагаются под углом 90⁰. Штриховка на них, изображенная на рис.7.5, показывает направление поляризации света. Луч белого света можно считать состоящим из нескольких лучей различных цветов с разной длиной волны. Поэтому при изучении модели в полярископе с источником белого света каждая его составляющая интерферирует после прохождения через анализатор, давая на экран полосы разной окраски. Одноцветные полосы на экране полярископа, проходящие через изображение модели, называют изохроиами, которые являются геометрическим местом точек с одинаковой разностью главных нормальных напряжений. На экране видна модель, покрытая разноцветными полосами. В некоторых точках неоднородно напряженной модели направление одного из главных нормальных напряжений совпадает с плоскостью поляризации поляроида 2, тогда луч света, проходя через модель, не будет разлагаться на два луча, а сохранит свою плоскость поляризации. Поскольку у него на пути к экрану стоит скрещенный поляроид, то этот луч гасится. На экране будут видны темные полосы. Темные полосы на экране полярископа, проходящие через изображение одели, называются изоклинам, являющимися геометрическим местом точек с одинаковым направлением главных нормальных напряжений. Физические явления поляризации света и искусственного двойного лучеприломления, которые изложены выше (метод фотоупругости), также положены в основу метода фотопластичности, который позволяет исследовать механизм пластической деформации: он позволяет получать экспериментальные данные о распределении напряжений, деформаций и скоростей деформаций в макрообъемах сплошной среды, используя достижения теории пластичности и феноменологической реологии. В основе метода лежит эффект двойного лучепреломления, который проявляется в некоторых прозрачных материалах при возникновении в них напряжений и деформаций. При просвечивании таких материалов поляризованным светом возникают оптические явления, позволяющие связать наблюдаемую картину с механическим состоянием тела. Применение данного метода связано с проблемой создания материалов, обладающих определенным комплексом оптико-механических свойств. Однако моделирование пластических деформаций (фотопластичность) до сих пор сдерживается из-за отсутствия соответствующих материалов.

Основные требования, предъявляемые к фотопластичным материалам, которые могут быть использованы в данном методе (по В.К.Воронцову): механическая и оптическая однородность; высокая пластичность; соответствие реологического поведения материала модели и реологическому поведению натуры; наличие определенной связи между оптическим эффектом (допустим, линейной разностью хода δ (см. рис.7.5) и напряжением σ, деформациями ε, скоростями деформаций ζ, температурой t т.е. δ = Φ (σ,ε,ζ,t). Для изготовления фотопластичных моделей используют целлулоид, полистирол, поликарбонатную смолу, нитрат целлюлозы и другие высокомолекулярные аморфные соединения.

Если теория моделирования плоской задачи фотоупругости успешно решена, то моделирование упруго-пластических и пластических деформаций методом фотопластичности до сих пор сдерживается из-за отсутствия соответствующих материалов модели и переноса результатов исследования с фотопластичной модели на натуру.

Метод оптически чувствительных покрытий. Трудностей моделироваиия и переноса результатов моделирования с фотопластичной модели на натуру удается избежать применяя новое экспериметальное направление в фотопластичности, основанное на использовании метода прозрачных оптически чувствительных покрытий (слоев или пленок), наклеиваемых на поверхность реального пластически-деформируемого металлического объекта. Этот метод получил название как метод оптически чувствительных покрытий. Согласно этому методу, на поверхность исследуемого объекта наносится тонкий слой оптически чувствительного материала, что позволяет применить поляризационно-оптический метод для изучения непрозрачного объекта. Основные положения метода для решения упругих задач были разработаны в 30-х годах XX в., однако широкое применение метода стало возможным только в 60-х годах благодаря появлению новых полимерных материалов, которые обладают необходимыми оптикомеханическими свойствами и сравнительно просты в использовании.П.И.Полухин, В.К.Воронцов, Р.М.Голубчик и др. [21] использовали метод оптически чувствительных покрытий для исследования напряженно-деформированного состояния заготовки при винтовой прокатке, выбрав в качестве модели реальный очаг деформации промышленного прошивного стана, который ограничен валками, линейками или роликами (рис.7.6).

 

 

Рис.7.6. Схема моделирования процесса винтовой прокатки при оптическом методе исследования (П.И.Полухин, В.К.Воронцов): 1-5 – сечения очага деформации [21]

В результате проведенных авторами исследований было установлено, что в осевой зоне заготовки в направлении приложения нагрузки Р по оси оz действуют напряжения сжатия (-s_z), а в перпендикулярном направлении по оси оу действуют растягивающие напряжения (+s_у)..С переходом от деформаций упругих к пластическим и с увеличением степени деформации диска величина растягивающих напряжений увеличивается, следовательно, увеличивается и коэффициент жесткости схемы напряженного состояния k_ж, т.е. напряженное состояние становится менее благоприятным и опасным с точки зрения возможного нарушения сплошности эаготовки. Для такой схемы прокатки по данным В.К.Воронцова коэффициент жесткости 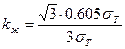меньше величины k_ж при

одноосном напряженном состоянии. По мнению В.К.Воронцова, определяющим фактором, влияющим на самопроизвольное вскрытие полости при поперечной прокатке является накопление остаточных напряжений, малоцикловая усталость при наличии знакопеременной нагрузки, которая создается разноименной схемой напряженного состояния и за N циклов деформации заготовки коэффициент k_ж увеличивается в центре заготовки до k_ж > 1,15

7.3 Методы исследования деформаций.

Наиболее распространенным методом исследования деформаций по сечению и объему зоны деформации является метод координатных сеток. Суть метода заключается в том, что на свободную поверхность исследуемого тела или на его внутреннюю поверхность наносят систему геометрических рисок, различных меток в виде линий (рис.7.7) или каких-либо других меток, положение которых соответствует выбранной системе координат: декартовой или полярной.

Рис 7.7. Схема измерения деформированной координатной сетки

Наибольшее распространение получили сетки, состоящие из взаимно перпендикулярных линий с равным шагом, что связано с достаточной простотой их получения и обработки экспериментальных данных. Исследуемый образец разрезают по плоскости симметрии. На одной половине образца наносят координатную сетку (чаще резцом). Половины образцов складывают и заваривают или запаивают по его периферии. После деформации образец разделяют на две части и по изменению формы и размеров ячеек координатной сетки судят о деформации данного тела. Если остановить процесс деформации образца, то после его разделения можно судить о последовательности изменения формы и размеров ячеек в различных стадиях процесса деформации. Например, для осесимметричного процесса ОМД достаточно знать координаты точек вдоль линии тока, выраженных в виде функции (см. рис.7.7) вида

R_i,j = Φ (R_j z_i)

где r_i,j и z_i – цилиндрические координаты текущих значений материальной точки М, расположенных на линии тока при ∆z = const (эйлеровы координаты); R_j – начальные координаты материальной точки (лагранжевы координаты).

Использование комбинированных координат, устанавливающих связь начальных R_j с текущими r_i,j, z_i координатами в виде производных первого порядка, позволяет получить простые выражения для радиальной v_r, осевой v_z скоростей течения и скоростей деформации ζ_ij Недостатком метода является относительно низкая чувствительность, поэтому его применяют при исследовании конечных этапных и полных деформаций, превышающих 5%. Верхний предел измеряемых деформаций может достигать и ≥ 100%.

Метод линий тока является разновидностью метода координатных сеток. Он основан на возможности описания установившихся несжимаемых течений с помощью функций тока, которая представляется визуально траекториями движения отдельных частиц. Это позволяет использовать одно семейство координатных линий, совпадающих с направлением течения материала. Особенности и области применения метода линий тока те же, что и метода координатных сеток. Видоизменением метода координатных сеток является метод винтов, вкручиваемых в исследуемый образец. После разрезки образца величину деформации в месте расположения винта определяют по изменению расстояния между витками резьбы.

Для исследования деформаций одновременно в нескольких слоях образца используют слоистые модели, которые выполняют из свинца или пластилина.

Метод муаровых полос (метод визиопластичности) был предложен Э.Томсеном, К.Янгом и Ш.Кобияши [22] для определения деформированного и напряженного состояний в стационарных процессах плоского или осесимметричного течения. Сущность метода заключается в том, что опытным путем устанавливают векторное поле скорости перемещения частиц в очаге деформации. Для этого, например, на плоскость разъема образца, подвергшегося малой деформации не до конца, наносят белые и черные полосы, которые называют растром. Обычно промежутки между полосами небольшие (от 4 до 40 линий /мм), так что растры воспринимаются глазом в виде равномерного серого фона. Большая плотность решеток требует специального оптического оборудования.

Метод муаровых полос занимает промежуточное место в экспериментальных методах исследования напряженно-деформированного состояния между оптическим методом и методом координатных сеток [23]. В основу метода положена механическая интерференция, возникающая при наложении деформированной вместе с образцом густой, мелкой сетки на исходную недеформированную эталонную сетку. Предварительно эталонную сетку фотографическим методом переносят на поверхность исследуемого образца, который затем подвергают пластической деформации. Деформированный образец (его поверхность с сеткой) фотографируют. Наложение пленок с эталонно и деформированной сеткой дает муаровый эффект – муаровые полосы (рис.7.4), в которых измеряют перемещения узловых точек сетки ΔU (ΔU_x и ΔU_Y). Поскольку деформация мала, то ΔU приближенно пропорционально скорости V, поэтому V = ΔU/Δ t (Δt = d /V₀; d – смещение жесткой части образца при малой деформации, V₀ – скорость этого смещения).

 

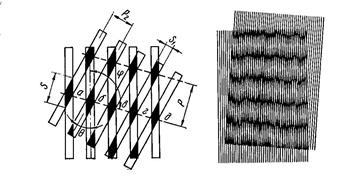
Рис.7.4 Образование эффекта муара при наложении линейных растров с вращением

Дальнейший ход определения деформированного состояния по методу визиопластичности состоит в следующем. Полученные в узловых точках сетки образца значения компонентов скорости V_x и V_y математически обрабатывают. На основании опыта аппроксимируют функциональную связь V_x = V_x (x, y) и V_y = V_y (x, y). Далее обычным путем вычисляют компоненты тензора деформации

ζ_ij = (v_i,j + v_j,I) / 2; i,j = x, y (7.2)

Авторы метода визиопластичности, получив картину деформированного состояния по известным формулам, пытаются определить напряженное состояние. Для этого с помощью физических уравнений вычисляют девиатор напряжений в каждой точке образца.

S_i,j = 2Т(H)ζ / Н; i, j = x, y (7.3)

где для несжимаемого материала Н = 2ζ_i,j ζ_i,j; Т = Т(Н) – известная функция, описывающая единой кривой реологические свойства модели. Если было бы известно значение среднего нормального напряжения σ в каждой точке, то задача расчета напряженного состояния была бы решена, так как σ_i,j = S_i,j + σδ_i,j. Поэтому для решения расчета напряжений методом муар отдельные авторы для конкретной задачи обработки металлов давлением (линейной, плоской, осесимметричной) применяют (произвольно) разные дифференциальные уравнения равновесия, в которых имеются достаточно четкие граничные условия. Такой подход к решению данной задачи в ряде случаев является необоснованным и не дает реальный результат.

Известны также и другие методы, которые в ОМД получили название как структурно наследственные методы. Структурно наследственные методы не дают достаточно полного и точного описания определенных свойств деформированной структуры и получить количественную оценку некоторых параметров пластически деформированного тела. Однако в некоторых случаях их применение целесообразно при исследовании реальных материалов и процессов без нарушения сплошности тел. Одним из таких методов является

выявление линий скольжения путем травления деформированных металлов в специальных реактивах или наблюдение их на полированной поверхности образца. Наилучшие результаты получаются на малоуглеродистых сталях, а также на металлах, имеющих зуб текучести при небольших пластических деформациях. При значительных пластических деформациях отдельные линии становятся неразличимыми, но могут быть установлены форма и границы пластических областей. Линии скольжения являются траекториями максимальных деформаций сдвига и во многих случаях совпадают с математическими характеристиками системы уравнений, описывающих пластическое течение. Так как задание характеристик эквивалентно построению решения, то оно оказывается исключительно полезным при анализе напряженного и деформированного состояний. Физическое выявление линий скольжения связано с именами Д.К.Чернова, Людерса и Гертмана. Применение данного метода позволило ряду авторам решить ряд задач по исследованию процессов ковки и штамповки.

К структурно наследственным методам относится также метод оценки интенсивности деформации сдвига по выпадению карбидов или количеству α – фазы в процессе деформации некоторых сталей.

Известен также метод определения интенсивности напряжений в произвольной точке деформированного образца путем измерения твердости [2], однако его применение связано со специальными способами и необходимостью использования других экспериментальных методов. Следует отметить, что эти методы не находят применения в экспериментальной механике, т. к. требуют специальной аппаратуры и не обеспечивают требуемой точности.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: