 |
Указания по выполнению задачи 3
|
|
|
|
Развертки многогранников строятся на листе формата A3 (297x420) Развертка прямой примы. Для построения развертки прямой призмы поступают следующим образом:
а) проводят горизонтальную прямую;
б) от произвольной точки G на этой прямой откладывают отрезки GK,
КЕ, EU, UG равные длинам сторон основания призмы;
в) из точек G, К, Е, U восставляют перпендикуляры (ребра призмы) и на
них откладывают отрезки, равные высоте призмы Концы перпендикуляров
соединяют прямой линией. Прямоугольник GG1 G1G является разверткой
боковой поверхности призмы;

|
13. Горизонтально-, фронтально-, профильно-проецирующая плоскость.
14. Биссекторная плоскость;
15. Горизонтальная, фронтальная, профильная плоскость;
16. Плоскость общего (произвольного) положения;
17. Плоскость уровня;
18. Прямая линия общего (произвольного) положения;
19. Горизонтальная, фронтальная, профильная прямая;
20. Горизонтально-, фронтально-, профильно-проецирующая прямая;
21. Горизонталь, фронталь, линия наибольшего ската;
22. След прямой;
23. След плоскости.
Студент должен уметь решать следующие позиционные задачи:
1. Построить недостающую проекцию точки;
2. Построить следы прямой линии;
3. В плоскости провести прямую общего положения, горизонталь, фронталь, прямую наибольшего ската;
4. Построить проекции точки, принадлежащей плоскости;
5. Определить - принадлежит ли плоскости точка, прямая;
6. Через точку провести плоскость общего положения;
7. Через заданную прямую провести горизонтально-, фронтально-проецирующую плоскость;
8. Построить следы плоскости, заданной двумя параллельными или пересекающимися прямыми;
9. Через точку провести плоскость, параллельную заданной плоскости.
|
|
|
10. Построить линию пересечения плоскостей, заданных следами;
П. Через точку провести прямую, параллельную заданной плоскости;
12. Через точку провести плоскость, параллельную заданной прямой
линии;
13. Построить точку пересечения прямой с плоскостью, заданной следами, параллельными прямыми, пересекающимися прямыми;
14. Из точки опустить перпендикуляр на плоскость,
15. Через точку провести плоскость, перпендикулярную заданной прямой;
16. Через точку провести плоскость, перпендикулярную заданной плоскости;
17. Совместить плоскость с плоскостью проекций;
18. Построить точку на поверхности многогранника.
Студент должен уметь решать следующие метрические задачи:
19. Определить натуральную величину отрезка методами совмещения, плоскопараллельного переноса, замены плоскостей проекций, вращения;
20. Определить величину линейного угла;
|
г) для получения полной развертки поверхности призмы к развертке боковой поверхности пристраивают многоугольники ее оснований.
Для построения на развертке линии пересечения призмы с пирамидой -замкнутых ломаных линий 123и45678- пользуются аппликатами точек. Например, для определения положения точки 1 на развертке поступают так: на отрезке UG от точки G влево откладывают отрезок Gl0 равный отрезку G11 (рис. 2). Из точки 10 восставляют перпендикуляр к отрезку UG и на нем откладывают аппликату Z точки 1. Аналогично строят и находят остальные точки.
Ртвертка пирамиды На рис. 2 определяют натуральную величину каждого из ребер пирамиды. Зная натуральные величины ребер пирамиды. строят последовательно натуральные величины ее граней. Зная натуральные величины граней, строят развертку. На ребрах и на гранях (на развертке) определяют вершины пространственной ломаной линии пересечения пирамиды с призмой.
Ребра многогранников и линии их пересечения обвести основной линией, вырезанные части ребер пирамиды и линии вспомогательных построений -сплошной тонкой линией.
|
|
|
Поименованные точки на развертках изобразить в виде кружков. На всех чертежах в графе основной надписи "номер чертежа" указывается после букв ДЗ (домашнее задание) с точкой - порядковый номер задания (01) и через точку - номер варианта, например, 01. В графе "Листов" указывается количество чертежей в задании (3), в графе "Лист" - номер задачи.
Основную надпись выполнить согласно требованиям ГОСТ 2.104-68. Размеры основной надписи и пример заполнения даны на рис. 4.
Для успешного выполнения и защиты задания студент должен иметь четкое представление о том. что такое:
1. Проекция точки;
2. Плоскость проекций.
3. Проецирующая прямая.
4. Проецирующая плоскость;
5. Проецирующий цилиндр;
6. Центральное проецирование:
7. Параллельное проецирование;
8. Ортогональное проецирование:
9. Квадрант;
10. Октант:
11. Эпюр Монжа;
12 Горизонтальная, фронтальная, профильная плоскость проекций:
|
| Продолж. табл.2 2 | |||||||||
| № | D | E | G | ||||||
| Вар. | X | У | Z | X | Y | Z | X | У | Z |
| 50. | |||||||||
| 39. | |||||||||
18 30 0 103 72 50 22 137 110 91
Таблица 3
Варианты задачи 2.
Координаты вершин пирамиды ABCD (мм)
| N9 | А | В | С | D | ||||||||
| вар. | X | У | Z | X | У | Z | X | У | Z | X | У | Z |
| 5!) | ||||||||||||
| 4() |

|
Таблица 1
|
|
|
Варианты заданий к задаче 1
Координаты вершин треугольника ABC
| № | А | В | С | ||||||
| вар. | X | У | Z | X | У | Z | X | У | Z |
| П9 | |||||||||
| о | |||||||||
Таблица 2
Варианты заданий к задаче 1.
Координаты вершин треугольника DEG
| № | D | Е | G | ||||||
| вар. | X | У | Z | X | Y | Z | X | У | Z |
I
|
|
|

|
|
|
Продолж. табл. 3 Координаты вершин основания четырехгранной призмы EKGU (мм)
| № | Е | К | G | U | ||||
| вар. | X | Y | X | У | X | У | X | У |
Примечания:
1 Высота призмы h = 85 мм;
2. Для всех вершин основания призмы координата Z = 0

|


|

|
|
КОНТРОЛЬНАЯ РАБОТА № 2 (листы 4, 5)
Содержание работы
Задание состоит из двух задач.
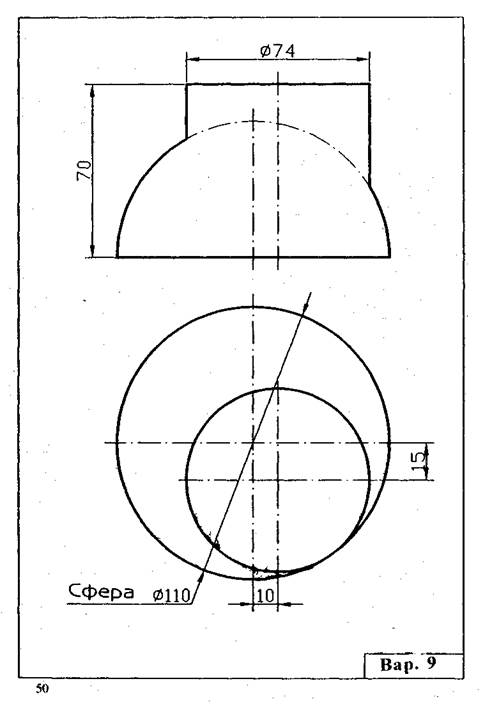
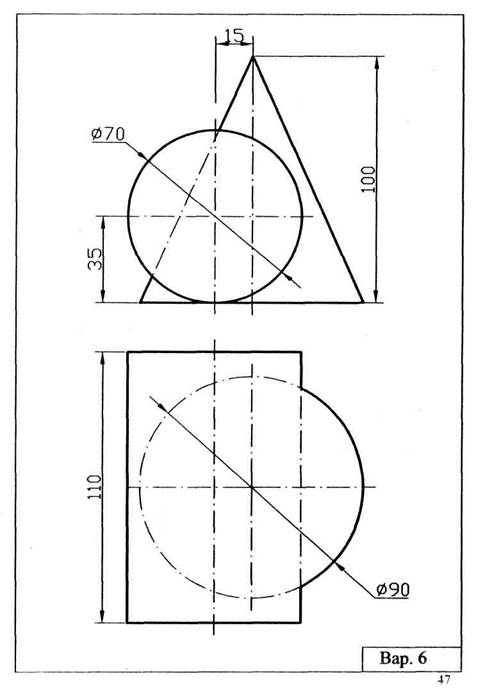
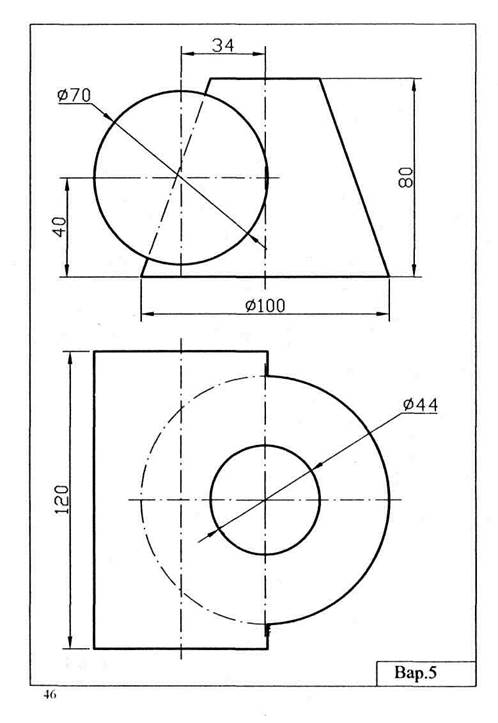
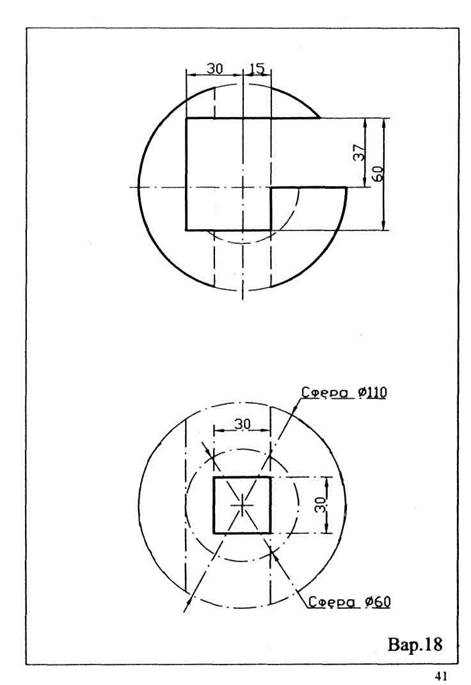
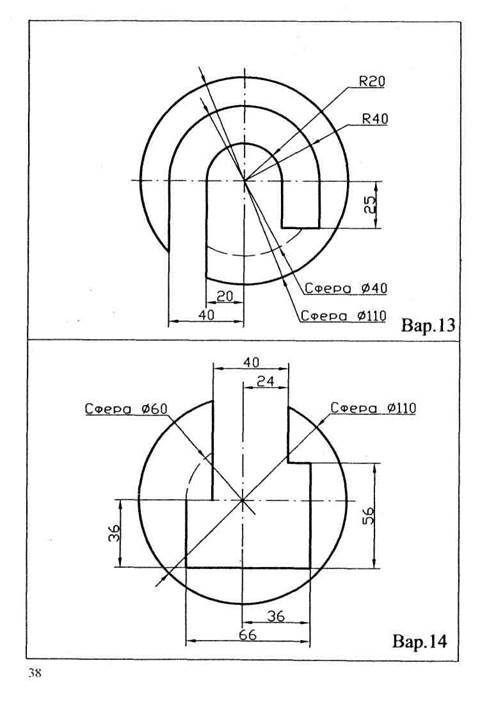
Задача 4 (лист 4). На трехпроекционном чертеже построить недостающие проекции сквозных пазов и отверстий в полом шаре. Стороны отверстий образованы фронтально- или горизонтально-проецирующими плоскостями и цилиндрами. Варианты заданий приведены ниже.
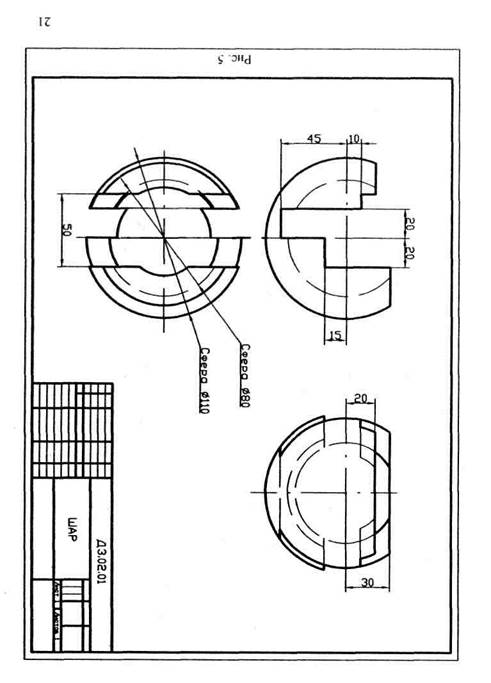
Задача 5 (лист 5). На трехпроекционном чертеже построить линии пересечения поверхностей вращения способом секущих плоскостей (пример выполнения показан на рис. 9) или способом секущих сфер (пример выполнения показан на рис. 10). Варианты заданий приведены ниже.
Общие указания по выполнению работы
Задачи выполняются на листах чертежной бумаги формата A3. Все построения проводятся вначале сплошными тонкими линиями. Видимость поверхностей определяется способом конкурирующих точек. Невидимые контуры следует показать штриховыми линиями. После проверки выполняют обводку чертежа линиями, соответствующими требованиям ГОСТ 2.303-68. Толщину основной линии (линии видимого контура, внутренняя рамка формата, толстые линии основной надписи) взять равной 0.8. остальных линий - 0,3.
Все буквенные и цифровые обозначения на поле чертежа выполняют шрифтом №5 по ГОСТ 2.304-81.
Основную надпись выполнить согласно требованиям ГОСТ 2.104-68.
На чертежах в графе основной надписи "номер чертежа" у называется после букв ДЗ (домашнее задание) с точкой - порядковый номер задания (02) и через точку - номер варианта, например. 01. В графе "листов" указывается количество чертежей в задании (2), в графе "лист" - порядковый номер листа (1).
|
|
|
Лист 4. Пример компоновки показан на рис. 5
Для успешного выполнения задачи 1 необходимо знать следующие положения из начертательной геометрии.
Сфера или шаровая поверхность образуется вращением окружности вокруг оси, проходящей через ее центр (рис. 6). Очерком сферы на фронтальной плоскости является главный меридиан, на профильной - профильный меридиан, на горизонтальной - экватор.
Главный меридиан делит сферу на переднюю - видимую и заднюю -невидимую части на фронтальной проекции. Профильный меридиан - на 20

|

|
 |

|
верхнюю видимую и нижнюю невидимую на горизонтальной проекции
Линией пересечения сферы с плоскостью является окружность. Окружность, получающаяся от сечения сферы плоскостью общего положения. проецируется на все плоскости проекций в виде эллипсов.
Если секущая плоскость параллельна плоскости проекций, (плоскость уровня), то на данную плоскость проекций окружность проецируется в натуральную величину. На другие плоскости проекций - в виде отрезков. равных диаметру окружности и параллельных осям координат, как покачано на рис.7.
Если секущая плоскость является проецирующей, то на соответствующую плоскость окружность проецируется в виде отрезка, равного диаметру окружности, а на другие плоскости - в виде эллипсов.
Например, на рис. 8 сфера рассечена фронтально-проецирующей плоскостью Р. Построить проекции сечения можно следующим образом.
Фронтальная проекция сечения сливается со следом-проекцией секущей плоскости и ограничена точками 12 и 22 в которых плоскость пересекает главный меридиан сферы. Отрезок 12 - 22 равен диаметру окружности сечения. Разделив его пополам (опустив на него перпендикуляр из центра сферы), получим проекцию центра этой окружности - точку С.
Горизонтальная проекция сечения представляет собой эллипс, для построения которого нужно, прежде всего, найти его оси
Построим горизонтальные проекции точек 1 и 2. которые лежат на главном меридиане сферы. Прямая 12 – 22 является проекцией того диаметра окружности сечения, который имеет наибольший наклон к горизонтальной плоскости проекций. Этот диаметр проецируется на горизонтальную плоскость с наибольшим искажением и, следовательно, прямая 12 – 22 будет малой осью эллипса.
Большой осью эллипса является тот диаметр окружности, который проецируется без искажения Это отрезок 3-4. который параллелен горизонтальной плоскости проекций. Точки 31 и 41 на горизонтальной проекции находим при помощи вспомогательной плоскости Т, проходящей через точку С и рассекающей сферу по окружности
Кроме точек 1, 2, 3, 4, характерными для кривой являются точки 5 и 6, которые лежат на экваторе сферы. Они делят горизонтальную проекцию эллипса на верхнюю видимую и нижнюю невидимую части.
Промежуточные точки можно построить при помощи вспомогательных секущих плоскостей так же, как построены точки 7 и 8
Недостающие проекции точек, лежащих на сфере (рис. 6). можно найти, проводя параллели. Так, например, найдены проекции А1 и А3 точки А, расположенной на передней верхней части сферы. Параллель, на которой лежит точка А, получена в результате пересечения сферы горизонтальной 22

|
|

|

|

|
|

|
плоскостью Р, проведенной через заданную фронтальную проекцию точки А.
Ниже даны варианты домашних заданий
Лист 5. Примерыкомпоновки показан на рис. 9 и рис. 10
Для построения линий пересечения поверхностей вращения (линий перехода) существует два способа - способ вспомогательных секущих плоскостей и способ вспомогательных секущих сфер. Рассмотрим их на примерах.
Способ секущих плоскостейзаключается в том. что две поверхности вращения рассекаются рядом параллельных плоскостей, пересекающих обе данные поверхности по прямым или окружностям. Пересечения этих последних линий дают точки, принадлежащие искомой линии пересечения
На рис. 9 изображены конус и полусфера. Требуется построить проекции линии их пересечения.
Очевидные точки их пересечения - это точка 12 которая лежит на пересечении очерковой образующей конуса и фронтальном мередиане сферы. и точка 21 - точка пересечения очерковых проекции оснований фигур.
Построение промежуточных точек показано на рис. 11 Здесь горизонтальная плоскость Р пересекает конус и полусферу по окружностям, которые проецируются на фронтальную плоскость в виде прямых линий (рис 11, а, б), а на горизонтальную - в виде окружностей. В случае пересечения данных поверхностей (рис 11, с) эти окружности, лежащие в одной плоскости. пересекутся в точках 11 и 21 которые являются общими для обеих поверхностей и, следовательно, принадлежат линии пересечения Фронтальные проекции точек пересечения (точки 12 и 22) строятся с помощью проекционной связи.
Для определения видимости линии пересечения на профильной проекции необходимо определить точку “вхождения” очерковой образующей конуса в сферу. На фронтальной проекции это будет, очевидно, точка 32 (рис. 9). Построив профильную проекцию точки 3, получим видимые участки линии пересечения от точки 23 и ей симметричной до точки 33 и ей симметричной.
|
|
|


