Экспериментальная установка

Лабораторная работа № 204.

ИЗУЧЕНИЕ ГИСТЕРЕЗИСА

ФЕРРОМАГНИТНЫХ МАТЕРИАЛОВ

 

Цель работы. Изучение гистерезиса ферромагнитных материалов, расчет и построение основной кривой намагничивания, расчет работы перемагничивания и коэрцитивной силы.

 

Методика измерений.

Все вещества обладают магнитными свойствами, т.е. являются магнетиками. Магнитные свойства веществ определяются величиной и ориентацией магнитных моментов молекул, ионов или атомов. Магнитный момент р плоского контура площадью S, по которому течет ток /, определяется по формуле

p = ISn (1)

где п - единичная нормаль, направление которой определяется по правилу правого винта. В магнитном поле с индукцией В на замкнутый контур с током действует механический момент:

(2)

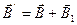которой стремиться повернуть контур так, чтобы направления и совпадали. Контур с током создает также собственное магнитное поле с индукцией , совпадающее по направлению с магнитным моментом контура. В устойчивом состоянии контура, когда , вектор индукции , в любой точке плоскости внутри контура всегда больше вектора индукции внешнего магнитного поля. Увеличение индукции внутри контура с током в магнитном поле качественно объясняет увеличение индукции в ферромагнетике, помещенном во внешнее магнитное поле.

Намагничивание вещества объясняется наличием у составляющих его атомов, молекул ионов микроскопических магнитных моментов: электронного орбитального 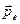, электронного собственного (спинового) . Электронным орбитальным магнитным моментом обладает электрон, движущийся вокруг ядра атома (рис. 1) Такой электрон подобен плоской круговой рамке с током

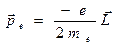I = ev, имеющий магнитный момент где е - заряд электрона, v - частота вращения, г - радиус круговой орбиты. Направление магнитного момента 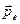противоположно направлению механического момента количества движения (рис.1). 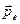и связаны соотношением,где т_е - масса электрона.

 

Рис. 2.

Рис. 1.

 

 

Спиновой магнитный момент (см.рис.1) является неотъемлемым свойством электрона. Единицей магнитного момента является магнетон Бора:

где — постоянная Планка.

При отсутствии поля приближенно можно считать, что магнитный момент атома

(3)

где Z — число электронов в атоме.

Магнитный момент молекулы 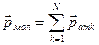, где N- число атомов в молекуле.

Во внешнем магнитном поле на электрон атома, как на контур с током, действует момент сил М (см.рис.2). Под действием этого момента сил орбита электрона, подобно механическому волчку, будет совершать прецессию, при которой векторы и описывают с постоянной угловой скоростью конусом вокруг направления поля. Это дополнительное движение электрона приводит к появлению у него магнитного момента прецессии , направленного против магнитного поля . Это явление носит название диамагнитного эффекта. При наличии внешнего магнитного поля магнитный момент атома

(4)

Намагниченность равна магнитному моменту единицы объема магнетика:

(5)

где V - малый объем магнетика; - сумма магнитных моментов всех молекул в объеме V. Намагниченность J связна с напряженностью магнитного поля:

(6)

где χ - коэффициент пропорциональности, называемый магнитной восприимчивостью вещества. Магнитные свойства характеризуются также магнитной проницаемостью μ. χ и μ связаны соотношением

μ = 1 + χ (7)

В зависимости от знака и величины магнитной восприимчивости все вещества делятся на три группы:

1. Диамагнетики - вещества (например, инертные газы), у которых при отсутствии внешнего магнитного поля орбитальные 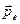и спиновые моменты атомов или молекул скомпенсированы. Во внешнем магнитном поле в результате прецессии появляются индуцированные магнитные моменты , направленные против поля, а магнитная восприимчивость отрицательна χ = -(10^-6...10^-8).

2. Парамагнетики - вещества, у которых при отсутствии внешнего поля или , а = 0 вследствие хаотической ориентации магнитных моментов или 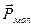. Во внешнем магнитном поле под действием вращающегося момента сил магнитные моменты ( и 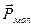) вещества стремятся провернуть в направлении поля, в результате чего J>0 и

3. Ферромагнетики - это кристаллические вещества, у которых магнитные моменты отдельных ионов . Магнитный момент иона ферромагнетика обусловлен упорядоченной ориентацией спиновых магнитных моментов.

 

а) б) Н 0 в) О

 

Рис. 3.

Часть ферромагнетика, в которой все магнитные моменты при отсутствии внешнего поля устанавливаются в одном направлении за счет обменного взаимодействия, называется доменом (рис.3,а). Домен обладает магнитным моментом . Размеры доменов составляют 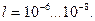При отсутствии внешнего магнитного поля магнитный момент ферромагнетика

Между доменами А и В имеются переходные слои С (рис. 3, б) шириной Внутри переходного слоя магнитные спиновые моменты ионов поворачиваются до тех пор, пока не примут нужного направления. Во внешнем магнитном поле переходные слои разрушаются. Магнитные моменты отдельных доменов поворачиваются в направлении магнитного поля (рис.3, в).

Зависимость намагниченности J магнетиков от напряжения Н внешнего магнитного поля изображена на рис. 4. Нелинейная область I отражает процесс ориентации доменов в ферромагнетиках в направлении внешнего поля при возрастании напряженности H. В сильных полях (область П) наступает магнитное насыщение и намагниченность практически не зависит от напряженности поля Н. Кривая J=f (H) линейная.

 

ферромагнетики

 

диамагнетики

Рис.4. Рис.5.

 

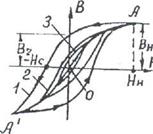
У ферромагнетиков имеет место магнитный гистерезис, в котором проявляется зависимость намагниченности от предшествующего состояния. При циклических изменениях величины и направления напряженности внешнего поля Н эта зависимость характеризуется кривой, называемой петлей гистерезиса (рис.5,кривые 1, 2, 3). Если ферромагнетик был первоначально размагничен (B=0, H=-H_c), то его намагничивание происходит по основной кривой намагничивания ОА. В точке А напряженность Н_H и индукция В_H соответствует состоянию магнитного насыщения его размагничивание происходит по кривой I (А-В_r-Н_c-А^”). При H=0 намагниченность ферромагнетика не исчезает B=B_R. Это состояние называется остаточным магнетизмом. Напряженность (-Н_C), при которой исчезает остаточная намагниченность (В=0, Н= - Н_C), принято называть коэрцитивной силой.

Рис. 6.

Если при циклическом намагничивании Н_тях > Н_H, то мы получаем максимальную петлю гистерезиса I. Кривые 2 и 3 это частные циклы, когда H_max < H_H. Максимумы В и Н частных циклов лежат на основной кривой намагничивания ОА. Условно принято считать ферромагнетики жесткими, если H_C < 100 А/м. Если H_C < 100 А/м, ферромагнетики считаются мягкими. Магнитная проницаемость μ ферромагнетика зависит от напряженности магнитного поля H (рис.6). Магнитная проницаемость μ = В/ μН₀ достигает максимума, когда напряженность Н внешнего поля становится равной напряженности H, при которой домены максимально ориентируются по направлению поля (см. рис.3, в) и при этом достигается магнитное насыщение образца.

 

Экспериментальная установка

PQ - звуковой генератор,

РО - электронный осциллограф,

ФПЭ - 07 - кассета.

 

 

РО

Рис.7.

Принципиальная схема установки приведена на рис. 7. Исследуемый образец выполнен в виде тороидального трансформатора Т, первичная обмотка которого содержит N₁ витков, а вторичная - N₂ витков. Напряжение на первичную обмотку трансформатора Т подается с выхода звукового генератора PQ через сопротивление R₁. Вторичная обмотка трансформатора последовательно соединена с сопротивлением R₂ и конденсатором С. С сопротивления R₁ на выход усилителя горизонтального отклонения осциллографа РО подается напряжение U_x, пропорциональное напряженности магнитного поля H На вертикальный выход «У» с конденсатора С подается напряжение U_у, пропорциональное индукции магнитного поля В. При радиусе витка обмотки r_в << r_m радиуса тороида напряженность H в тороиде

(8)

где r_m =(r₁ + r₂)/2; r₁=d₂ /r₂; r₂=d₂/2.

Так как падение напряжения на сопротивлении R₁

U_x = I₁R₁ , то с учетом (8)

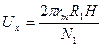(7.9)

(9)

U_x определяется по коэффициенту отклонения электронного луча по горизонтальной оси k_x

U_x=k_xx (10)(7.10)

С учетом (10) выражение для H может быть записано в виде

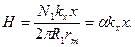(11)

По закону Фарадея ЭДС индукции по вторичной обмотке

(12)

где Ф - поток вектора магнитной индукции через один виток; S₂ - площадь поперечного сечения тороида.

По закону Кирхгофа для вторичной обмотки получаем:

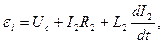(7.13)

(13)

где Uc - напряжение на конденсаторе; - ток во вторичной обмотке; L₂ - индуктивность вторичной обмотки.

Так как L₂ очень мало, a >> U_c, уравнение (13) может быть записано с учетом (12) в следующем виде:

= .

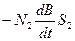Откуда

(14)(14)

 

Учитывая (14), найдем напряжение , равное напряжению на конденсаторе

(15)

где g - заряд на обкладках конденсатора.

Если известен коэффициент отклонения луча 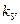по вертикали, то

. (16)(7.16)

Из выражения (15) и (16) получаем

(17)

Подав одновременно напряжения и на вертикально и горизонтально отклоняющие пластины, получим на экране осциллографа петлю гистерезиса.

По площади петли можно найти работу перемагничивания, отнесенную к единице объема. Измерение объемной плотности энергии магнитного поля

в цикле перемагничивания определяется по формуле

. (18)

Работа dA_n расходуется на изменение внутренней энергии единицы объема ферромагнетика. За полный цикл перемагничивания

. (19)

Учитывая (11) и (17), получаем

(20)

где S_m - площадь петли гистерезиса; S₂=(r₁-r₂)b.

 

Порядок выполнения работы

Задание 1. Определение основной кривой намагничивания.

 

1. Установить на стенде приборы, указанные на рис.8.

2. Ознакомившись с описанием установки и методом измерения, соединить приборы в соответствии со схемой, изображенной на рис.8.

3. Ознакомиться с работой звукового генератора PQ и электронного осциллографа РО в режиме измерения фигур Лиссажу.

4. Подготовить приборы к работе:

а) установить следующие параметры выходного сигнала звукового генератора: 2 кГц - частота; выходное напряжение - 0,

б) отключить развертку на осциллографе РО.

5. Включить лабораторный стенд и приборы. Установить луч в центре экрана осциллографа, после чего, регулируя величину выходного напряжения на
звуковом генераторе и усиление по оси У, установить максимальную петлю гистерезиса в пределах экрана, соответствующую магнитному насыщению
образца. Уменьшая величину выходного напряжения, получить семейство петель гистерезиса (см. рис.5) - не менее 5 петель. Для каждой петли
снять координаты «X» и «У» ее вершины и записать их в таблицу 1

 

Рис.8.

Таблица 1
№ петли	Х, м	У, м	Ux, B	Uy, B	H0, A/м	H, A/м	В, Тл	В, Тл

 

6. По формулам (11) и (17) вычислить значения напряженности H и индукции В вершин каждой петли гистерезиса и записать их в таблицу.
Значения d₁, d₂, N₁, N₂, R₁, R₂ и b указаны на панели кассеты ФПЭ - 07.

7. Оценитьдоверительную границу случайной погрешности измерения H и В при доверительной вероятности Р=0,9, связанную с погрешностью величин
k_х, k_у, X, У. Погрешность измерения величин H и В определяется:

а) приборными погрешностями коэффициентов отклонения электронного луча k_х, k_у и погрешностями визуального отсчета величин X и У на экране осциллографа (по паспорту на осциллограф k_х=±0,01k_х , k_у=±0,01k_у , Х= У=0,5мм);

б) погрешность величин N₁, N₂, R₁, R₂, Z_m, S₂, С (она существенного вклада в общую погрешность не дает);

 

Задание 2. Оценка работы перемагничивания А _п за один цикл.

 

1. Получить максимальную петлю гистерезиса и зарисовать на кальке в координатах X и У.

2. Скопировать эту петлю на миллиметровую бумагу, измерить ее площадь.

3. Определить работу перемагничивания за один цикл по формуле (20).

 

Задание 3. Определение коэрцитивной силы.

 

1. По максимальной петле гистерезиса найти координату - Х_с, соответствующую коэрцитивной силе - Н_с (см. рис.5).

2. По формуле (11) рассчитать Н_с.

3. По полученному значению определить группу ферромагнетика (мягкий или жесткий). По формуле (21) оценить погрешность измерения коэрцитивной силы.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

 

1. Как ведет себя контур с током в магнитном поле?

2. Каковы свойства парамагнетиков, диамагнетиков, ферромагнетиков?

3. Какова причина спонтанной намагниченности доменов в ферромагнетиках?

4. Как ведут себя домены при увеличении напряженности внешнего магнитного поля? Что означает насыщение ферромагнетика?

5. В чем заключается явление магнитного гистерезиса?

6. Физический смысл площади петли гистерезиса?

 

 

Поделиться:

Воспользуйтесь поиском по сайту: