 |
Характеристика распределения признака в статистической сов-ти. Типы распределения.
|
|
|
|
Абсолют. величины нужны для ОБЩ. ХАР-КИ, напр,числ-ть нас-я
в мире, в стране, в городе и т. п.
Относит. величины нужны для СРАВНЕНИЯ:
= экстенсивные показатели- хар-ют структуру явлений(структура
заболе-ти, смерт-ти, инвал-ти и т.д.).
экстенс. = часть явления *100(%)
пок-ль явление в целом
Напр, структура = число б-х онкол. ЖКТ *100
онкол. заб-ний все онкол. больные
= интенсивные показатели – служит для хар-ки
частоты(интенсивн-ть, уровень,распрстр-ть) явлений в
среде, кот-я непоср-но продуц-ет это явл-е(демогр. пок-ли,
абс. размер явления *(100,1000,10000)(‰)
ИП= абс. размер среды, кот. подуц-ет это явл-е
Напр, уровень = число заболевших * 1000(‰)
заб-ти числ-ть нас-я
= пок-ль соотношений- хар-ет частоту явлений в среде,кот. не
продуцирует это явл-е
абс. размер явления *(100,1000,10000)
ПС= абс. размер среды, кот. не подуц-ет это явл-е
Напр, уровень = число врачей * 1000
обеспеч-ти врачами в г. Москва нас-е г. Москва
= динамич. ряд –совокупность однородных статистич. величин,
показывающих изменение какого-то явления(признака) во
времени.
Числа, из кот. сос-ся дин. ряд, м. б. абсолютными,
относительными, средними величинами.
Если дин. ряд сост. из абсолют. величин- простой.
Если из относит. или средних – сложный или производный.
Осн. показатели дин. ряда:
Абсолбютный прирост(убыль)- разность м/ду последующим и
предыдущим уровнями.
Темп прироста(убыли)- процентное отношение абсол.
прироста каждого послед. уровня к предыдущему уровню, прнятому за 100%.
Показатель роста (убыли) – отношение каждого послед. уровня к предыдущему, принятому за 100%
Показатель наглядности – это отношение каждого послед-го к начальному уровню, принятому за 100 %.
Методы выравнивания динам. ряда:
|
|
|
= укрупнение интервала
= вычисление скользящей средней
= вычисление скользящей средней по Урбаху.
Типы распределения:
1.Альтернативное(для качеств. признаков)-исход лечения: выж.,
умер.;
2. Симметричное(норм-е,для колич. признаков)-бол-во изуч. явл-й
3. Ассиметричное(Для колич. пр.)
4. Правостороннее(число детей в семье)
5. Левостороннее(кратность рививок)
6. Двугорбое (бимодальное)-неоднородная группа.
60. Выборочные исследования. Определение необходимого числа наблюдений. Пути формирования выборочной совокупности.
Выборочное исследование является на сегодняшний день очень актуальным, поскольку сокращает объем работ по сбору и обобщению данных, сокращает сроки получения конечных результатов, позволяет сводить к минимуму порчу и уничтожение изделий при проверке их качества а также используется для контроля и уточнения данных сплошного наблюдения.
Для определения объема выборки, способа ее отбора, правил переноса выборочных результатов контроля на всю совокупность применяются методы, разработанные в теории статистического контроля.
Выборочный контроль работы сотрудников также может быть полезен. При этом наряду с выборкой людей полезна и выборка из совокупности дел, которыми занимается данный сотрудник.
1. Общие понятия и определение необходимого объема выборки
1.1. Сущность теории выборки
Сама по себе идея выборок была известна очень давно. Еще в 1949 г. М. Кенуем предложил метод исключения одного наблюдения. При этом для выборки объема n получаем n "похожих" на нее выборок объема (n - 1) каждая. Если же исключать по 2 наблюдения, то число "похожих" выборок возрастает до n (n - 1) / 2 объема (n - 2) каждая.
На основе этого метода была сформулирована следующая простая практическая рекомендация.Предположим, что Вы по выборке делаете какие-либо статистические выводы. Вы хотите узнать также, насколько эти выводы устойчивы. Если у Вас есть другие (контрольные) выборки, описывающие то же явление, то Вы можете применить к ним ту же статистическую процедуру и сравнить результаты. А если таких выборок нет? Тогда Вы можете их построить искусственно. Берете исходную выборку и исключаете один элемент. Получаете похожую выборку. Затем возвращаете этот элемент и исключаете другой. Получаете вторую похожую выборку. Поступив так со всеми элементами исходной выборки, получаете столько выборок, похожих на исходную, каков ее объем. Остается обработать их тем же способом, что и исходную, и изучить устойчивость получаемых выводов - разброс оценок параметров, частоты принятия или отклонения гипотез и т.д.
1.2. Основные понятия выборочного исследования
Выборочный метод применяется в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. В частности, проверка качества отдельных видов продукции может быть связана с ее уничтожением (оценка крепости нити на разрыв, дегустация продуктов питания и т. п.); другие совокупности настолько велики, что было бы физически невозможно собрать данные в отношении каждого из их членов (например, при изучении пассажиропотоков или цен на рынках, исследованиях бюджетов семей). Выборочное наблюдение используют также для проверки результатов сплошного наблюдения.
Ту часть единиц, которые отобраны для наблюдения, принято называть выборочной совокупностью, а всю совокупность единиц, из которых производится отбор, — генеральной. Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо иной фактор, кроме случая.
Существуют различные методы формирования выборочной совокупности. Это собственно случайный, механический, типический, серийный, комбинированный.
Собственно случайный отбор заключается не в преднамеренном отборе единиц для исследования, при этом число отобранных единиц определяется исходя из принятой доли выборки.
Собственно случайный отбор проводится при помощи жеребьевки, розыгрышей, лотереи, таблицы случайных чисел. Недостатком этого способа является то, что при проведении отбора нужно иметь перечень всех единиц генерации совокупности. Этот способ применяется для изучения небольшой совокупности
Механический отбор. Отбор единиц производится из генеральной совокупности разбитой предварительно на равные группы. Затем из каждой группы выбирают одну единицу. Размер группы равен обратной величине доли выборки.
Например, при 5% отборе выборку попадет каждая 20-я единица.
Для обеспечения репрезинтативной в выборке все единицы генеральной совокупности должны быть расположены в алфавитном порядке. Генеральная совокупность может быть упорядочена по существенному второстепенному и нейтральному признаку.
Типический отбор - генеральная совокупность делится на однородные типические группы из которых собственно случайным или механическим способом производится отбор единиц.Типический отбор дает самые точные результаты по сравнению с другими способами, т.к. обеспечивается репрезентативность в выборке. Например, рабочие делятся на группы по квалификации.
Серийный отбор – с генеральной совокупности отбираются не отдельные единицы, а целые серии, группы, а затем в каждой попавшей в выборку серии обследуются все без исключения единицы. Например, рабочих отбирают бригадами.
Комбинированный отбор – генеральная совокупность делится на одинаковые группы, затем производится отбор групп из которых отбираются отдельные единицы.
1.3. Определение ошибок выборки
Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации возникают из-за неправильных или неточных сведений. Источниками таких ошибок могут быть непонимание существа вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности, описки при заполнении формуляров и т. д.
Среди ошибок регистрации выделяются систематические, обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам, сотням и т. д.), и случайные, проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.
Ошибки репрезентативности также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки — принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между характеристиками выборочной и генеральной совокупности. Изучение и измерение случайных ошибок репрезентативности и является основной задачей выборочного метода.
1.4. Определение численности выборки
Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность формулы для определения численности выборки (п) зависят от метода отбора.
Объем выборки можно рассчитать по следующей формуле:
|
|
|
|
|
|
|
|
|
ni = 
где ni – объем выборки из I – й группы;
n – общий объем выборки;
Ni - объем i – й группы;
N - объем генеральной совокупности.
2. Практическая часть
При проведении выборочного наблюдения статистическая совокупность из которой производится отбор единиц генеральной совокупностью, а единицы отобранной – для исследования выборной совокупностью (выборкой).
N – число единиц генеральной совокупности;
n – число единиц выборки.
Например, из 2000 рабочих завода для определения выполнения выработки отобрано 200 человек.
N – 2000;
n – 200 – 10%.
При отборе должен соблюдаться принцип репрезентативности (представительности), т.е. в выборку должны попасть единицы из всех групп имеющихся в генеральной совокупности.
Для обобщающей характеристики генеральной и выборной совокупности используются относительные и средние величины.
Для характеристики совокупности по альтернативному признаку используются относительные величины, которые рассчитываются в виде доли тех единиц, которые обладают изучаемым признаком.
Генеральная доля:  .
.
Выборочная доля:  .
.
М, m – число единиц, обладающих изучаемым признаком.
|
|
|
Для характеристики совокупности по варьирующему признаку применяются средние величины:
 Генеральная средняя
Генеральная средняя 
 .
.
Выборочная средняя  .
.
Рассмотрим на примере, насколько отличаются выборочные и генеральные показатели по данным о выполнении рабочими нормы выработки:
Из 2000 рабочих – 300 человек выполнили норму на 90%;
600 человек – 100%;
500 человек – 110%;
400 человек – 120%;
200 человек – 130%.
Из 200 отработанных рабочих – 24 человека – 90%.
59 человек – 100%;
52 человека – 110%;
43 человека – 120%;
22 человека – 130%;
24 человека – 90%.
Доля рабочих не выполнивших норму (с выработкой менее 100%):
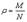 =
= 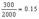
 =
= 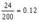
Средняя норма выработки:
 =
= 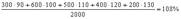
 =
=  Следовательно, разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности
Следовательно, разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности
61. Малая выборка. Особенности расчета статистических критериев в малой выборке.
Малые выборки, статистические выборки столь малого объема n, что к ним нельзя применить простые классические формулы, действующие лишь асимптотически при n ® ¥. Особенности статистической оценки параметров по Малые выборки легче всего понять на примере нормального распределения (для которого малыми обычно считают выборки объема n £ 30). Пусть необходимо оценить неизвестное среднее значение a выборки x1, x2,..., xn из нормальной совокупности с неизвестной дисперсией s2. Обозначим
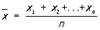 ,
,
 .
.
Исходным пунктом при оценке a служит то обстоятельство, что распределение вероятностей величины
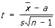
не зависит от а и s.
Вероятность w неравенства - t w < t < t w и равносильного ему неравенства
 (1)
(1)
вычисляется при этом по формуле
w =  (2)
(2)
где s (t, n - 1) есть плотность вероятности для так называемого Стьюдента распределения с n - 1 степенями свободы. Определяя для заданных n и w (0 < w < 1) соответствующее t w (что можно сделать, например, по таблицам), получают правило (1) нахождения доверительных границ для величины а, имеющей значимости уровень w.
При больших n формула (2), связывающая w и t w, приближенно может быть заменена формулой
 (3)
(3)
Эту формулу иногда неправильно применяют для определения t w при небольших n, что приводит к грубым ошибкам. Так, для w = 0,99 по формуле (3) находим t0,99 = 2,58; истинные значения t 0,99 для малых n приведены в следующей таблице:
| n< | 2< | 3< | 4< | 5< | 10< | 20< | 30< |
| t 0,99 | 63,66 | 9,92 | 5,84 | 4,60 | 3,25 | 2,86 | 2,76 |
Если пользоваться формулой (3) при n = 5, то получится вывод, что неравенство
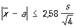
выполняется с вероятностью 0,99. В действительности в случае пяти наблюдений вероятность этого неравенства равна лишь 0,94, а вероятностью 0,99 обладает в соответствии с приведенной таблицей неравенство
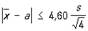
Об оценке по Малые выборки теоретической дисперсии s2 см. "Хи-квадрат" распределение. Разработаны также аналогичные методы оценки по Малые выборки параметров многомерных распределении (например, коэффициента корреляции).
|
|
|


