 |
О некоторых трудностях, возникающих при решении геометрических задач
|
|
|
|
В.Ф.Чаплыгин
Анализ результатов приемных экзаменов в университет, опыт работы со школьниками, слушателями подготовительных отделений, студентами-математиками, готовящими себя к педагогической деятельности, дают основания сделать вывод о том, что при решении текстовых задач учащиеся испытывают значительно больше трудностей, чем при решении уравнений и неравенств. Это отчасти объясняется тем, что для решения уравнений, неравенств или их систем можно использовать некоторый набор известных алгоритмов и приемов, так как сама задача уже формализована, математизирована. А для текстовой задачи математическую модель учащийся должен составить самостоятельно. И поэтому эти задачи, в том числе геометрические, о которых пойдет речь, требуют существенно больших логических усилий. Мы коснемся здесь, в основном, задач на вычисление.
Решение более или менее серьезной задачи требует, во-первых, тщательного ее анализа. Учащийся должен ясно осознать, что же ему известно, как связаны между собой данные величины, какие следствия из них можно получить, что необходимо найти в задаче и что требуется для этого знать. Анализ при этом может носить не только однонаправленный характер (от данных величин к искомым или наоборот), но и встречный, когда движение совершается в двух противоположных направлениях.
Трудным моментом является выбор метода, который приведет к решению задачи наикратчайшим путем. Он, как правило, не однозначен и почти каждая задача допускает не одно решение (имеется в виду не результат, а процесс). Рассуждения, используемые для решения, могут быть чисто геометрические или позаимствованные из алгебры или тригонометрии. К сожалению, приходится констатировать слабые знания учащимися простейших утверждений, фактов, формул. Они затрудняются в измерении углов, связанных с окружностью (вписанных, центральных, составленных хордой и касательной, образованных хордами, пересекающимися внутри окружности, или секущими, исходящими из одной точки вне окружности), не знают свойств касательных и секущих, вписанных и описанных многоугольников, теорем синусов и косинусов, связь значений тригонометрических функций с отношениями сторон прямоугольного треугольника. Хорошо известно, что немаловажную роль в решении геометрических задач имеет чертеж. Если он выполнен верно, то поможет в правильном выборе решения, если ошибочен, то может навести на ложный путь. Говоря об этом, мы не призываем к тому, чтобы включать в курс школьной геометрии как можно больше теорем (на все случаи жизни), а предлагаем создавать комплексы задач, сгруппированных по принципу общих идей или методов решения. Решая задачу, следует обращать внимание учащихся на моменты, помогающие правильно выбрать способ решения, прививать вкус к таким задачам, вселять веру в их творческие возможности, развивать логические способности и интуицию.
|
|
|
Приведем примеры задач, которые нам представляются интересными. Первые три задачи используют подобие.
Задача 1. Прямоугольный треугольник АВС с катетами АС=3, ВС=2 вписан в квадрат. Известно, что вершина А совпадает с вершиной квадрата, а вершины В и С лежат на сторонах квадрата, не содержащих точку А. Найти площадь квадрата.
 В силу равенства отмеченных углов (рис.1) треугольник ACD подобен треугольнику CBE
В силу равенства отмеченных углов (рис.1) треугольник ACD подобен треугольнику CBE 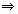
 . Пусть AD=x, тогда DC=
. Пусть AD=x, тогда DC=  . Так как AD2+DC2=AC2, то x2+
. Так как AD2+DC2=AC2, то x2+  =9, x2=
=9, x2=  . Таким образом, площадь квадрата равна
. Таким образом, площадь квадрата равна  .
.
Задача 2. На сторонах BC и CD квадрата ABCD выбраны соответственно точки E и F так, что 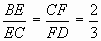 и К - точка пересечения отрезков BF и AE. Найти отношение КЕ:АК.
и К - точка пересечения отрезков BF и AE. Найти отношение КЕ:АК.
 Из подобия треугольников (рис.2) AKB, BKE и ABE следует
Из подобия треугольников (рис.2) AKB, BKE и ABE следует  . Перемножив равенства
. Перемножив равенства  и
и  , получим
, получим  .
.
|
|
|
Эту задачу можно решить с помощью гомотетии или теоремы Фалеса, но, на наш взгляд, предложенное решение предпочтительнее.
Задача 3. Диаметр окружности с центром О лежит на стороне AD четырехугольника ABCD, при этом АО=ОD. Три остальные стороны АВ, ВС и СD касаются этой окружности. Найти AD, если АВ =а и CD=b.
 Пусть в треугольнике АВО (рис.3) ВАО=, АВО=, ВОА= и, следовательно, + + =. Так как ВО - биссектриса угла СВА, то СВО=.
Пусть в треугольнике АВО (рис.3) ВАО=, АВО=, ВОА= и, следовательно, + + =. Так как ВО - биссектриса угла СВА, то СВО=.
Если Р и Q - точки касания, то APO= DQO (они прямоугольные, ОР=ОQ, AO=OD) QDO= PAO=. Сумма углов четырехугольника ABCD равна 2, поэтому С=2 –2 –2.
А так как СО - биссектриса, то DCO= –( +)=. Таким образом, треугольники АОВ и DCO подобны и  . Отсюда получаем равенства АО· OD=AB· CD=ab АО=OD=
. Отсюда получаем равенства АО· OD=AB· CD=ab АО=OD=  и AD=2
и AD=2  .
.
А в следующих двух задачах учащиеся должны вспомнить свойства вписанных и описанных четырехугольников.
Задача 4. На стороне ВС параллелограмма ABCD выбрана такая точка Е, что  =2. Известно, что трапеция AECD обладает следующими свойствами:
=2. Известно, что трапеция AECD обладает следующими свойствами:
1) в нее можно вписать окружность;
2) около нее можно описать окружность.
Найти величину угла BAD.
 В силу свойств, которыми обладает трапеция AECD (рис.4), она равнобокая (АЕ=CD) и 2АЕ=ЕС+AD.
В силу свойств, которыми обладает трапеция AECD (рис.4), она равнобокая (АЕ=CD) и 2АЕ=ЕС+AD.
Пусть ВС=3а, тогда BE=2a, EC=a 2AE=EC+AD=4a CD=АЕ=2a.
Таким образом, BEA - равносторонний ABC=60 BAD=120.
Далеко не все учащиеся могут доказать, почему трапеция, около которой можно описать окружность, является равнобокой.
Задача 5.Сумма углов при основании ВС трапеции ABCD равна  . Найти величину
. Найти величину  , если известно, что
, если известно, что  =10 и в трапецию ABCD можно вписать окружность.
=10 и в трапецию ABCD можно вписать окружность.
 Пусть CF AB (рис.5), тогда CF=AB и в силу условия задачи следует,
Пусть CF AB (рис.5), тогда CF=AB и в силу условия задачи следует,
что FCD=  .
.
По теореме косинусов
FD2=FC2+СD2-2FC· СDcos  (AD–BC)2=AB2+СD2– AB· СD. (1)
(AD–BC)2=AB2+СD2– AB· СD. (1)
Так как в трапецию ABCD можно вписать окружность, то
AD+BC=AB+CD (AD+BC)2=(AB+СD)2. (2)
Разделив равенство (1) на равенство (2), получим
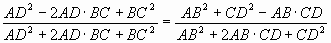 .
.
Разделив далее числитель и знаменатель левой дроби на произведение AD· BC, а правой части - на AB· СD, получим
 .
.
Откуда, положив  =t, и учитывая, что
=t, и учитывая, что  =10, имеем t=7.
=10, имеем t=7.
В этой задаче при неудачном выборе решения оно может оказаться очень громоздким.
|
|
|
Весьма поучительно, на наш взгляд, решение следующей задачи.
Задача 6. В прямоугольном треугольнике АВС из вершины прямого угла С проведена биссектриса CL и медиана СМ. Найти площадь треугольника АВС, если LM=a, CM=b.
 Пусть АС=х и ВС=у, где х>y (рис.6), тогда х2+у2=4b2, и по свойству биссектрисы
Пусть АС=х и ВС=у, где х>y (рис.6), тогда х2+у2=4b2, и по свойству биссектрисы  LB=
LB=  AB=
AB=  и, следовательно, ML=MB–LB=b–
и, следовательно, ML=MB–LB=b–  =
=  .
.
Таким образом, приходим к системе
 .
.
Решая это уравнение относительно ху, находим S ABC=  =
=  .
.
Следует обратить внимание учащихся на то, что из полученной системы уравнений искать значения переменных х и · у совершенно излишне.
Задача 7. Основание равнобедренного треугольника равно 10 см, проведенная к нему высота - 12 см. Вершины треугольника служат центрами кругов, каждый из которых касается двух других внешним образом. Найти радиусы кругов, которые касаются трех указанных кругов внешним и внутренним образом.
 Пусть e, f, d, k, h - точки касания, радиус окружности с центром в точке О1 равен r, а с центром в точке О2 - R (рис.7). Так как AD=5, АВ=13,
Пусть e, f, d, k, h - точки касания, радиус окружности с центром в точке О1 равен r, а с центром в точке О2 - R (рис.7). Так как AD=5, АВ=13,
то BE=8, BО1=8+r, AО1=5+r, О1D=4–r.
Из прямоугольного треугольника AO1D (5+r)2=25+(4–r)2, 18r=16, r=  .
.
ВО2=R–8, О2D=12–(R–8)=20–R, О2A=R–5,
и, следовательно, из прямоугольного треугольника АО2D имеем
(R–5)2=(20–R)2+25 R=  =13
=13 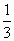 .
.
Здесь следует напомнить учащимся, что прямая, проходящая через центры двух касающихся окружностей, проходит через точку их касания.
В заключение приведем одну задачу на доказательство, которая требует от учащихся достаточно высокой логической культуры.
Задача 8. Докажите, что треугольник является равнобедренным в том и только в том случае, когда равны биссектрисы двух внутренних углов.
Если в треугольнике АВС (рис.6) АВ=ВС, то углы А и С равны и равны треугольники ВАЕ и ВСD, так как В - общий и ВАЕ= ВСD, следовательно, АЕ=СD.
 Докажем справедливость обратного утверждения. Пусть биссектрисы AE и CD углов А и С треугольника АВС равны. Докажем, что А= С. S АВС=S ВАЕ+S ЕАС
Докажем справедливость обратного утверждения. Пусть биссектрисы AE и CD углов А и С треугольника АВС равны. Докажем, что А= С. S АВС=S ВАЕ+S ЕАС  АВ· АС· sinА=
АВ· АС· sinА=  АВ· АЕ· sin
АВ· АЕ· sin  +
+  АЕ· АС· sin
АЕ· АС· sin  2· АВ· АСcos
2· АВ· АСcos  =(АВ+АС)АЕ АЕ=
=(АВ+АС)АЕ АЕ= 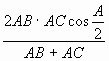 .
.
Разделив числитель и знаменатель дроби на произведение АВ· АС и обозначив
|
|
|
АВ=с, АС=b, ВС=a, получим  , аналогично, биссектриса
, аналогично, биссектриса  .
.
Если допустить, что А С, например, А< С, то сos  >cos
>cos  и а<c
и а<c  >
>  AE>CD, получили противоречие.
AE>CD, получили противоречие.
Приведенные в статье задачи предлагались на вступительных экзаменах в различных вузах России, в том числе, в Ярославском госуниверситете.
Список литературы
Пойа Д., Как решать задачу, М.: Учпедгиз,1961,207 с.
Смирнов Е.И., Технология наглядно-модельного обучения математике, Ярославль,1997,323с.
Чаплыгин В.Ф., Чаплыгина Н.Б., Задачи вступительных экзаменов по математике, Ярославль, 1991,140с.
Чаплыгин В.Ф., Чаплыгина Н.Б., Задачи вступительных экзаменов по алгебре и геометрии, Ярославль, 1999,112с.
Сборник задач по математике для поступающих в вузы (под ред. Прилепко А.И.), М.: Высшая школа,1989,271с.
Зафиевский А.В., Вступительные экзамены по математике в 1998году, Ярославль, 1999,36с.
Лидский В.Б., Овсянников Л.В., Тулайков А.Н., Шабунин М.Н., Задачи по элементарной математике, М.: Физматгиз, 1960, 463с.
Для подготовки данной работы были использованы материалы с сайта http://www.yspu.yar.ru
|
|
|


