 |
Гидравлические сопротивления
|
|
|
|
Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса. Особенности турбулентного движения жидкости. Пульсации скоростей и давлений. Распределение осредненных скоростей по сечению. Потери напора в трубах. Формула Дарси-Вейсбаха. Коэффициент потерь на трение по длине X. Шероховатость стенок – абсолютная и относительная. Графики Никурадзе и Мурина-Шевелева. Гидравлически гладкие и шероховатые трубы. Формулы для определения коэффициента потерь на трение и области их применения. Основные виды местных сопротивлений. Коэффициент местных потерь. Потери при внезапном расширении трубы (формула Борда).
Методические указания
Потери напора на трение по длине трубы при любом режиме движения жидкости определяют по формуле Дарси-Вейсбаха:
 или
или 
где  – коэффициент гидравлического трения;
– коэффициент гидравлического трения;  – длина расчетного участка трубы;
– длина расчетного участка трубы;  – диаметр трубы;
– диаметр трубы;  – средняя скорость.
– средняя скорость.
Неизвестной величиной при определении потерь на трение по длине является коэффициент  ; для его определения предложен следующий алгоритм:
; для его определения предложен следующий алгоритм:
1. Re<2300,  = 64/Re.
= 64/Re.
2. Диапазон 2300≤Re<4500 соответствует переходу от ламинарного режима к турбулентному. Трубопроводы, соответствующие этой зоне проектировать не рекомендуется.
3. Зона гладкостенного сопротивления соответствует интервалу 4500≤Re<10  ,
,  = 0,3164/Re0,25,
= 0,3164/Re0,25,  – эквивалентная шероховатость.
– эквивалентная шероховатость.
4. Диапазон 10  ≤Re<500
≤Re<500  соответствует зоне доквадратичного сопротивления, здесь
соответствует зоне доквадратичного сопротивления, здесь  =0,11(68/Re +
=0,11(68/Re +  )0,25.
)0,25.
5. При Re≥500  происходит переход к так называемой квадратичной зоне, здесь
происходит переход к так называемой квадратичной зоне, здесь  =0,11(
=0,11( )0,25.
)0,25.
Для труб промышленного изготовления с естественной шероховатостью для любой области сопротивления при турбулентном режиме движения можно пользоваться формулой А.Д. Альтшуля:
|
|
|
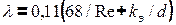 0,25
0,25
Местные гидравлические потери определяют по формуле Вейсбаха:
 или
или  .
.
где 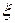 – коэффициент местного сопротивления;
– коэффициент местного сопротивления;  – средняя скорость в сечении, как правило, за местным сопротивлением. Коэффициент
– средняя скорость в сечении, как правило, за местным сопротивлением. Коэффициент 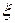 при больших числах Рейнольдса зависит только от вида местного сопротивления. Однако при ламинарном течении он зависит не только от вида сопротивления, но и от числа Рейнольдса. Для ламинарного движения коэффициент
при больших числах Рейнольдса зависит только от вида местного сопротивления. Однако при ламинарном течении он зависит не только от вида сопротивления, но и от числа Рейнольдса. Для ламинарного движения коэффициент 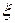 должен быть пересчитан с учетом влияния числа Рейнольдса.
должен быть пересчитан с учетом влияния числа Рейнольдса.
Простое суммирование потерь в местных сопротивлениях возможно, если они расположены друг от друга на расстоянии, равном не менее 20-30 диаметров трубы. В противном же случае сопротивления влияют друг на друга и работают как одна система, для которой необходимо определить свое значение коэффициента местного сопротивления экспериментальным путем.
Контрольные вопросы
1. На какие два вида делятся гидравлические сопротивления? По каким зависимостям они определяются (привести формулы Дарси-Вейсбаха и Вейсбаха, пояснив все входящие в них величины)?
2. Что служит критерием для определения режима движения жидкости? Какие числовые значения критического числа Рейнольдса для круглого напорного трубопровода принимают при практических расчетах?
3. Как распределяются скорости по живому сечению потока при ламинарном и турбулентном режимах движения жидкости в круглой трубе?
4. Какие существуют зоны гидравлического сопротивления? От каких параметров зависит коэффициент гидравлического трения в каждой из этих зон?
5. Что такое гидравлически «гладкие» и гидравлически «шероховатые» стенки? Объясните, почему эти понятия являются относительными.
6. Как зависят потери напора по длине от скорости при ламинарном движении режима и в квадратичный зоне сопротивления?
7. Что называется мгновенной местной скоростью и осредненной местной скоростью? Что такое осредненное турбулентное течение?
|
|
|
8. Приведите зависимости для коэффициента гидравлического сопротивления по длине для зон сопротивления: а) ламинарной; б) гладкостенной; в) доквадратичной; г) квадратичной.
9. Какой вид имеет формула Вейсбаха для определения местных потерь напора? Приведите примеры местных гидравлических сопротивлений.
10. Как формулируется теорема Борда для случая внезапного расширения потока?
ЗАДАНИЕ
| Группа б2-СТЗСз21 | Группа б2-СТЗСз22 |
| Задачи 1.2, 1.5, 1.6, 2.1, 2.5,5.1, 6.2 | Задачи 1.3, 1.4, 1.7, 2.2, 2.10,5.2, 6.1 |
Номер варианта в каждой задаче берется по последней цифре зачетной книжки.
Задачи
Набор I
Тип 1
Задача 1.1. Давление в баллоне с кислородом для газовой сварки при хранении его на улице, где температура  , °C, равно
, °C, равно  атм. Каково будет давление в баллоне при внесении его в помещение с температурой
атм. Каково будет давление в баллоне при внесении его в помещение с температурой  , °C?
, °C?
| № варианта | ||||||||||
 , °C , °C
| -30 | -27 | -25 | -25 | -20 | -15 | -12 | -10 | -7 | -5 |
 , °C , °C
| ||||||||||
 , атм , атм
|
Задача 1.2. Определить коэффициент температурного расширения воды 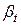 , если при увеличении температуры от
, если при увеличении температуры от  , °C, до
, °C, до  , °C, объем воды, равный
, °C, объем воды, равный  , увеличится на величину
, увеличится на величину  .
.
| № варианта | ||||||||||
 , °C , °C
| ||||||||||
 , °C , °C
| ||||||||||
 , м3 , м3
| ||||||||||
 , м3 , м3
| 0,005 | 0,006 | 0,007 | 0,009 | 0,011 | 0,012 | 0,020 | 0,025 | 0,040 | 0,041 |
Задача 1.3. Для периодического аккумулирования прироста воды, получающегося при изменении температуры, в системах водяного отопления устраивают резервуары, которые присоединяются к системе в верхней ее точке и сообщаются с атмосферой. Определить максимальный объем расширительного резервуара, чтобы он полностью не опорожнился. Допустимые колебания температуры воды во время перерывов в топке  . Объем воды в системе
. Объем воды в системе  . Принять значение коэффициента температурного расширения
. Принять значение коэффициента температурного расширения  равным
равным 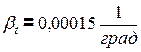 .
.
| № варианта | ||||||||||
 , °C , °C
| ||||||||||
 , м3 , м3
| 0,50 | 0,55 | 0,65 | 0,70 | 0,75 | 0,80 | 0,85 | 0,90 | 0,95 | 0,100 |
Задача 1.4. В отопительный котел поступает вода с расходом  при температуре
при температуре  , °C. Какой объемный расход воды
, °C. Какой объемный расход воды  будет выходить из котла, если нагрев производится до температуры
будет выходить из котла, если нагрев производится до температуры  (рис. 1)? Принять значение
(рис. 1)? Принять значение  коэффициента температурного расширения
коэффициента температурного расширения 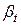 равным
равным  .
.
|
|
|
| № варианта | ||||||||||
 , м3/час , м3/час
| ||||||||||
 , °C , °C
| ||||||||||
 , °C , °C
|
Задача 1.5. Трубопровод длиной  и внутренним диаметром
и внутренним диаметром  перед гидравлическими испытаниями заполнен водой, находящейся под атмосферным давлением. Определить, сколько нужно добавить в трубопровод воды, чтобы избыточное давление в нем повысилось до величины
перед гидравлическими испытаниями заполнен водой, находящейся под атмосферным давлением. Определить, сколько нужно добавить в трубопровод воды, чтобы избыточное давление в нем повысилось до величины  . Деформацией трубопровода пренебречь.
. Деформацией трубопровода пренебречь.
| № варианта | ||||||||||
 , м , м
| ||||||||||
 , мм , мм
| ||||||||||
 , кг/см2 , кг/см2
|
Задача 1.6. В цилиндрическую емкость высотой  залили нефть при температуре
залили нефть при температуре  . Определить, до какого уровня можно налить нефть, если температура окружающей среды повысилась до
. Определить, до какого уровня можно налить нефть, если температура окружающей среды повысилась до  . Расширение емкости не учитывать; коэффициент температурного расширения для нефти принять равным
. Расширение емкости не учитывать; коэффициент температурного расширения для нефти принять равным 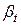 = 0,001°C-1.
= 0,001°C-1.
| № варианта | ||||||||||
 , м , м
| 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,5 | 4,0 | 4,5 | |
 , °C , °C
| ||||||||||
 , °C , °C
|
Задача 1.7. Установить, как изменится уровень нефти в вертикальном цилиндрическом резервуаре диаметром  при повышении ее температуры от
при повышении ее температуры от  до
до  . Вес нефти, хранящейся в резервуаре,
. Вес нефти, хранящейся в резервуаре,  . Плотность нефти
. Плотность нефти  = 870 кг/м3; коэффициент температурного расширения
= 870 кг/м3; коэффициент температурного расширения 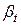 = 0,00068 1/К. Расширение резервуара не учитывать. Температуры
= 0,00068 1/К. Расширение резервуара не учитывать. Температуры  и
и  абсолютные.
абсолютные.
| № варианта | ||||||||||
 , м , м
| 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,2 | 3,3 | 3,4 | 3,5 |
 , °К , °К
| ||||||||||
 , °К , °К
| ||||||||||
 , Н , Н
| 5×105 | 6×105 | 7×105 | 8×105 | 9×105 | 9,2×105 | 9,4×105 | 9,6×105 | 9,8×105 | 10×105 |


|
 равномерного скольжения прямоугольной пластины (
равномерного скольжения прямоугольной пластины ( ) по наклонной плоскости под углом
) по наклонной плоскости под углом  = 12°, если между пластиной и плоскостью находится слой масла толщиной
= 12°, если между пластиной и плоскостью находится слой масла толщиной  (рис. 2). Плотность материала пластины
(рис. 2). Плотность материала пластины  = 650 кг/м3, кинематический коэффициент вязкости масла
= 650 кг/м3, кинематический коэффициент вязкости масла  = 0,87 см2/с, плотность масла
= 0,87 см2/с, плотность масла  = 920 кг/м3.
= 920 кг/м3.|
|
|
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
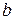 , мм , мм
| ||||||||||
 , мм , мм
| ||||||||||
 , мм , мм
| 1 | 2,5 | 3,5 | 4,5 | 5,5 | 5,6 |
Задача 1.9. Воздух сжат и его давление (избыточное) равно  , температура при этом равна
, температура при этом равна  °C. Определить его плотность.
°C. Определить его плотность.
| № варианта | ||||||||||
 , ат , ат
| 0,5 | 0,8 | 1,2 | 2,0 | 1,4 | 1,8 | 2,2 | 0,6 | 1,5 | 1,6 |
 °C °C
|
Задача 1.10. Жидкость, плотность которой  , обладает динамической вязкостью
, обладает динамической вязкостью  . Определить коэффициент кинематической вязкости
. Определить коэффициент кинематической вязкости  в м2/с, в см2/с, в стоксах.
в м2/с, в см2/с, в стоксах.
| № варианта | ||||||||||
 , кг/м3 , кг/м3
| ||||||||||
 , Па∙с , Па∙с
|
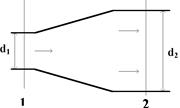
 Задача 2.1. Поток постепенно расширяется, переходя из трубы диаметром
Задача 2.1. Поток постепенно расширяется, переходя из трубы диаметром  в трубу диаметром
в трубу диаметром  (рис. 3). Скорость в сечении 1 с диаметром
(рис. 3). Скорость в сечении 1 с диаметром  равна
равна  . определить скорость
. определить скорость  в широком сечении.
в широком сечении.
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
 , мм , мм
| ||||||||||
 , м/c , м/c
| 3,5 | 3,4 | 3,3 | 3,2 | 3,1 | 3,0 | 2,9 | 2,8 | 2,7 | 3,0 |

 Задача 2.2. Поток постепенно расширяется, как показано на рис. 4, от круглого сечения диаметром
Задача 2.2. Поток постепенно расширяется, как показано на рис. 4, от круглого сечения диаметром  до круглого сечения диаметром
до круглого сечения диаметром  . Скорость в сечении 2 равна
. Скорость в сечении 2 равна  , м/с. Определить скорость в сечении 1.
, м/с. Определить скорость в сечении 1.
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
 , мм , мм
| ||||||||||
 , м/c , м/c
| 3,4 | 3,3 | 3,2 | 3,1 | 3,0 | 2,9 | 2,8 | 2,7 | 2,6 | 2,5 |

 Задача 2.3. Поток жидкости переходит из трубы диаметром
Задача 2.3. Поток жидкости переходит из трубы диаметром  в трубу диаметром
в трубу диаметром  (рис. 5); отношение скоростей
(рис. 5); отношение скоростей  и
и  равно
равно  . Определить отношение диаметров
. Определить отношение диаметров  .
.
| № варианта | ||||||||||

| 1,4 | 1,6 | 2,1 | 3,4 | 2,8 | 1,8 | 3,0 | 1,5 | 2,2 | 3,2 |

 Задача 2.4. В поток жидкости, имеющий площадь поперечного сечения
Задача 2.4. В поток жидкости, имеющий площадь поперечного сечения  и расход
и расход  , вливается другой поток той же жидкости с расходом
, вливается другой поток той же жидкости с расходом  . Определить площадь сечения бокового притока
. Определить площадь сечения бокового притока  и сечение потока после слияния
и сечение потока после слияния 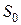 , считая скорости во всех сечениях одинаковыми.
, считая скорости во всех сечениях одинаковыми.
| № варианта | ||||||||||
 , м2 , м2
| 0,8 | 1,0 | 1,2 | 1,6 | 0,6 | 1,8 | 2,0 | 1,7 | 2,2 | 1,9 |
 , м3/с , м3/с
| 1,0 | 1,1 | 0,8 | 0,6 | 0,8 | 1,2 | 2,0 | 1,0 | 1,2 | 1,1 |
 , м3/с , м3/с
| 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 0,8 | 1,0 | 0,9 | 1,2 | 1,0 |
Задача 2.5. Определить среднюю скорость потока жидкости и число Рейнольдса в круглой трубе внутренним диаметром  , если при определении расхода объемным способом объем
, если при определении расхода объемным способом объем  был набран за время
был набран за время  . Температура воды
. Температура воды  (
( – абсолютная температура).
– абсолютная температура).
|
|
|
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
 , л , л
| 3,5 | 4,0 | 2,8 | 2,6 | 3,7 | 4,2 | 4,5 | 3,8 | 4,1 | 3,9 |
 , с , с
| ||||||||||

|
|
 до
до  ; определить отношение скоростей
; определить отношение скоростей  , если отношение диаметров равно
, если отношение диаметров равно  .
.
| № варианта | ||||||||||

| 1,2 | 1,6 | 1,4 | 1,8 | 1,8 | 1,5 | 1,4 | 1,6 | 1,4 |

 Задача 2.7. Определить число Рейнольдса в сечении 1, если в сечении 2 оно равно
Задача 2.7. Определить число Рейнольдса в сечении 1, если в сечении 2 оно равно  . Задано отношение диаметров
. Задано отношение диаметров  . Температура жидкости не изменяется при переходе от сечения 1 к сечению 2.
. Температура жидкости не изменяется при переходе от сечения 1 к сечению 2.
| № варианта | ||||||||||

| ||||||||||

| 3,0 | 2,6 | 2,2 | 2,0 | 2,8 | 2,1 | 1,8 | 3,0 | 2,4 | 2,6 |
Задача 2.8. По трубопроводу диаметром  перекачивают нефть, плотность которой
перекачивают нефть, плотность которой  . Средняя скорость потока в трубе равна
. Средняя скорость потока в трубе равна  . Определить массовый расход нефти.
. Определить массовый расход нефти.
Указание. Если  – объемный расход, то массовый расход
– объемный расход, то массовый расход 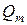 равен
равен  .
.
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
 , кг/м3 , кг/м3
| ||||||||||
 , м/с , м/с
| 0,8 | 0,9 | 1,2 | 1,0 | 1,5 | 1,4 | 0,8 | 1,0 | 1,6 | 1,2 |
Задача 2.9. В призматическом открытом канале прямоугольного сечения глубины по длине изменяются и в двух сечениях 1 и 2 равны соответственно  и
и  . Определить среднюю скорость
. Определить среднюю скорость  в сечении 2, если в сечении 1 она равна
в сечении 2, если в сечении 1 она равна  .
.
| № варианта | ||||||||||

| 1,2 | 1,4 | 1,6 | 1,3 | 1,5 | 1,7 | 1,8 | 2,0 | 1,2 | 1,8 |
 , м/с , м/с
| 0,5 | 0,6 | 0,7 | 1,0 | 2,3 | 2,0 | 1,6 | 1,2 | 1,3 | 1,8 |
Задача 2.10. При измерении расхода объемным способом за время  был набран объем
был набран объем  литров. Внутренний диаметр трубы, через которую поступала вода равен
литров. Внутренний диаметр трубы, через которую поступала вода равен  . Определить число Рейнольдса в потоке. Температура воды
. Определить число Рейнольдса в потоке. Температура воды  (
( – абсолютная температура).
– абсолютная температура).
| № варианта | ||||||||||
 , л , л
| 4,0 | 3,8 | 2,9 | 4,4 | 4,8 | 5,0 | 6,0 | 5,4 | 4,4 | 5,2 |
 , с , с
| ||||||||||
 , мм , мм
| ||||||||||

|
Задача 2.11. При течении воды в трубе диаметром  расход равен
расход равен  . Определить среднюю скорость и число Рейнольдса. Температура воды
. Определить среднюю скорость и число Рейнольдса. Температура воды  °C.
°C.
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
 , л/с , л/с
| 1,5 | 2,5 | 3,1 | 1,6 | 2,2 | 3,0 | 2,8 | 1,8 | 2,2 | 3,1 |
 °C °C
|
Задача 2.12. По трубопроводу диаметром  движется газ со средней скоростью
движется газ со средней скоростью  . Определить среднюю скорость движения на участке трубопровода диаметром
. Определить среднюю скорость движения на участке трубопровода диаметром  . Газ считать несжимаемым.
. Газ считать несжимаемым.
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
 , м/с , м/с
| ||||||||||
 , мм , мм
|
 Задача 2.13. Определить среднюю скорость потока (рис. 8) в сечении 1-1, если средняя скорость в сечении 2-2 равна
Задача 2.13. Определить среднюю скорость потока (рис. 8) в сечении 1-1, если средняя скорость в сечении 2-2 равна  , а отношение диаметров
, а отношение диаметров  задано.
задано.

| № варианта | ||||||||||
 , м/с , м/с
| 3,5 | 2,8 | 3,2 | 4,4 | 5,0 | 3,8 | 2,6 | 1,9 | 2,9 | 3,9 |

| 1,5 | 2,0 | 2,2 | 3,0 | 2,0 | 3,1 | 2,8 | 2,3 | 2,9 | 3,2 |
Задача 2.14. Определить среднюю скорость воды в круглой трубе и число Рейнольдса, если диаметр трубы  и объем
и объем  (литров) был набран в мерную емкость (при измерении расхода объемным способом) за время
(литров) был набран в мерную емкость (при измерении расхода объемным способом) за время  . Температура воды 20 °C.
. Температура воды 20 °C.
| № варианта | ||||||||||
 , мм , мм
| ||||||||||
 , л , л
| 4,2 | 3,3 | 2,8 | 4,0 | 3,6 | 4,2 | 3,8 | 4,2 | 3,2 | 5,2 |
 , с , с
|
Задача 2.15. Определить среднюю скорость воды в круглой трубе и расход в ней, если диаметр трубы равен  и число Рейнольдса равно
и число Рейнольдса равно  . Температура воды
. Температура воды  °C.
°C.
| № варианта | ||||||||||
 , мм , мм
| ||||||||||

| ||||||||||
 , °C , °C
|
Задача 2.16. Определить диаметр круглой трубы и расход, если при средней скорости воды  число Рейнольдса равно
число Рейнольдса равно  . Температура воды
. Температура воды  °C.
°C.
| № варианта | ||||||||||
 , м/с , м/с
| 1,2 | 1,4 | 1,0 | 1,6 | 2,0 | 2,2 | 2,4 | 1,8 | 1,3 | 1,5 |

| ||||||||||
 , °C , °C
|
Задача 2.17. Определить среднюю скорость потока  в сечении 2 после плавного расширения, если средняя скорость в сечении 1 равна
в сечении 2 после плавного расширения, если средняя скорость в сечении 1 равна  . Диаметры в узком и широком сечениях равны
. Диаметры в узком и широком сечениях равны  и
и  .
.
| № варианта | ||||||||||
 , м/с , м/с
| 25,5 | 20,3 | 19,4 | 16,2 | 10,2 | 12,0 | 11,0 | 9,0 | 8,0 | 3,5 |
 , мм , мм
| ||||||||||
 , мм , мм
|
Задача 2.18. По цилиндрической трубе диаметром  течет вода со средней скоростью
течет вода со средней скоростью  . Какое количество воды в единицу времени необходимо отвести из трубопровода, чтобы скорость движения снизилась до
. Какое количество воды в единицу времени необходимо отвести из трубопровода, чтобы скорость движения снизилась до  .
.
| № варианта | ||||||||||
 , м/м , м/м
| ||||||||||
 , м/с , м/с
| 5,6 | 3,5 | 6,0 | 4,2 | 3,2 | 2,6 | 1,6 | 0,6 | 0,8 | 1,0 |
 , м/с , м/с
| 3,0 | 2,0 | 4,0 | 0,6 | 3,0 | 1,2 | 0,7 | 0,2 | 0,4 | 0,5 |
Задача 2.19. Отношение чисел Рейнольдса в узком и широком сечениях круглой трубы  известно; известен также диаметр узкой части
известно; известен также диаметр узкой части


