 |
Законы распределения случайных величин.
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ ЗАОЧНЫЙ УНИВЕРСИТЕТ
(ФГБОУ ВО РГАЗУ)
Факультет Электроэнергетики и ТС
Контрольная работа
Метрология, стандартизация и сертификация
Регистрация Студент: Поляков Е.А.
Деканатом…………….. Направление подготовки 35.03.06
Кафедрой……………… Курс - 2*
Шифр – 2126
Балашиха 2020
Содержание
7.
35.
79.
120 
Список использованной литературы
Шероховатость поверхности, основные параметры.
Шероховатость поверхности - это совокупность неровностей поверхности с относительно малыми шагами, выделенная с помощью базовой длины.
1. Требования к шероховатости поверхности должны устанавливаться исходя из функционального назначения поверхности для обеспечения заданного качества изделий. Если в этом нет необходимости, то требования к шероховатости поверхности не устанавливаются и шероховатость этой поверхности контролироваться не должна.
2. Требования к шероховатости поверхности должны устанавливаться путем указания параметра шероховатости (одного или нескольких) из перечня значений выбранных параметров и базовых длин, на которых происходит определение параметров.
При необходимости дополнительно к параметрам шероховатости поверхности устанавливаются требования к направлению неровностей поверхности, к способу или последовательности способов получения (обработки) поверхности.
|
|
|
Для номинальных числовых значений параметров шероховатости должны устанавливаться допустимые предельные отклонения.
Допустимые предельные отклонения средних значений параметров шероховатости в процентах от номинальных следует выбирать из ряда 10; 20; 40. Отклонения могут быть односторонними и симметричными.
3. Требования к шероховатости поверхности не включают требований к дефектам поверхности, поэтому при контроле шероховатости поверхности влияние дефектов поверхности должно быть исключено. При необходимости требования к дефектам поверхности должны быть установлены отдельно.
Допускается устанавливать требования к шероховатости отдельных участков поверхности (например, к участкам поверхности, заключенным между порами крупнопористого материала, к участкам поверхности срезов, имеющим существенно отличающиеся неровности).
Требования к шероховатости поверхности отдельных участков одной поверхности могут быть различными.
4. Параметры шероховатости (один или несколько) выбирают из приведенной номенклатуры:
Ra - среднеарифметическое отклонение профиля;
Rz - высота неровностей профиля по десяти точкам;
Rmax - наибольшая высота профиля;
Sm - средний шаг неровностей;
S - средний шаг местных выступов профиля;
tp - относительная опорная длина профиля, где р - значение уровня сечений профиля.
Параметр Ra является предпочтительным.
5. Числовые значения параметров шероховатости (наибольшие, номинальные или диапазоны значений) выбирают из таблиц
6. Относительная опорная длина профиля tp:
10; 15; 20; 30; 40; 50; 60; 70; 80; 90 %.
7.Числовые значения уровня сечения профиля р выбирают из ряда:
5; 10; 15; 20; 25; 30; 40; 50; 60; 70; 80; 90 % от Rmax.
8. Числовые значения базовой длины l выбирают из ряда:
0,01; 0,03; 0,08; 0,25; 0,80; 2,5; 8; 25 мм.
Законы распределения случайных величин.
Определение cслучайной величиной называется переменная величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно. Пример Случайными величинами являются: температура больного в некоторое наугад выбранное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента.
|
|
|
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины 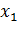 ,
, 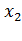 ,
,  ,… и соответствующими им вероятностями
,… и соответствующими им вероятностями 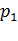 ,
, 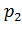 ,
, 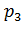 ,….
,….
Закон распределения может быть задан аналитическими, в виде таблиц или графически. Таблица соответствия значения случайной величины и их вероятностей называется рядом распределения.
Рассмотрим дискретную случайную величину X с возможными значениями x1, х2, …, хn. Каждое из этих значений возможно, но не достоверно, и величина X может принять каждое из них с некоторой вероятностью. В результате опыта величина X примет одно из этих значений, т. е. произойдет одно из полной группы несовместных событий. Рассмотрим дискретную случайную величину X с возможными значениями x1, х2, …, хn. Каждое из этих значений возможно, но не достоверно, и величина X может принять каждое из них с некоторой вероятностью. В результате опыта величина X примет одно из этих значений, т. е. произойдет одно из полной группы несовместных событий. Обозначим вероятности этих событий буквами р с соответствующими индексами: Р(Х=х1)=р1; Р(Х=х2) = р2;...; Р(Х = хn) = рn.
|
|
|


