 |
Построить сопряжение – значит найти центр сопряжения и точки сопряжения (точки касания линий).
|
|
|
|
ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ
Благовещенск
2007
Е.А.Гаврилюк, Л.А.Ковалева, А.В.Станийчук
ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ
Благовещенск
2007
ББК Печатается по решению
редакционно - издательского совета
Амурского государственного университета
Е.А.Гаврилюк, Л.А.Ковалева, А.В.Станийчук
Геометрическое черчение: Учебно-методическое пособие
Амурский гос. ун-т. Благовещенск, 2007
Пособие содержит основные правила выполнения геометрических построений на чертежах, методические указания и варианты заданий для выполнения графической работы №1 «Геометрическое черчение».
Пособие предназначено для студентов всех специальностей изучающих курс «Инженерная графика», «Инженерная и компьютерная графика», «Технический рисунок и начертательная геометрия».
© Амурский государственный университет, 2007
Содержание
Введение 5
1. Нанесение размеров 6
2. Сопряжения линий 13
3. Лекальные кривые 16
4. Методические указания по выполнению графической работы
|
|
|
«Геометрическое черчение» 22
5. Некоторые характерные ошибки 23
Литература 25
Приложение. Варианты заданий 26
ВВЕДЕНИЕ
Задание «Геометрическое черчение» входит в комплекс графических
Работ, выполняемых студентами по курсу «Инженерная графика».
Целью выполнения задания является:
1) приобретение студентами навыков по выполнению чертежей технических
форм, очертания которых требуют построения конусностей, уклонов, со-
пряжений различного вида;
2) приобретение навыков построения лекальных кривых линий с использованием лекал;
3) закрепление навыков простановки размеров на деталях различного вида.
Нанесение размеров
Все изображения сопровождаются нанесением размеров. При нанесении размеров следует руководствоваться основными положениями ГОСТ 2.307- 68.
На чертеже проставляются размеры истинной величины детали и ее элементов независимо от масштаба, в котором выполнены изображения.
Линейные размеры указываются на чертеже в миллиметрах без обозначения единицы измерения, угловые — в градусах, минутах и секундах с обозначением единицы измерения.
Для нанесения на чертеже размеров проводят выносные и размерные линии (сплошные тонкие линии S/3 – S/3). При нанесении размера прямолинейного отрезка размерную линию проводят параллельно этому отрезку, а выносные линии — перпендикулярно размерным. Размерные линии предпочтительно наносить вне контура изображения. Не допускается использовать в качестве размерных линии контура, центровые и выносные линии. Необходимо избегать пересечения размерных и выносных линий. Размерную линию ограничивают с обоих концов стрелками, упирающимися в выносные, осевые или контурные линии.
|
|
|
При нанесении размера угла размерная линия проводится в виде дуги с центром в его вершине, а выносные линии — радиально.
Выносные линии проводят от линий видимого контура. Выносные линии должны выходить за концы стрелок размерной линии на 1...5 мм.
Расстояние между линией контура и размерными линиями выбирается в зависимости от размеров изображения и насыщенности чертежа. Минимальное расстояние размерной линии от параллельной ей линии контура должно быть 10мм, а минимальное расстояние между параллельными размерными линиями — 7мм (рис.1).
Размерные числа наносят над размерной линией возможно ближе к ее середине. При нанесении нескольких параллельных размерных линий на небольшом расстоянии друг от друга размерные числа следует располагать в шахматном порядке.

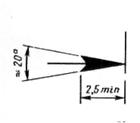
Рис.1
При указании диаметра окружности независимо от того, изображена она полностью или частично, допускается проводить размерные линии с обрывом. Обрыв делают за центром окружности (рис. 2).

Рис. 2
Линейные размеры при различных наклонах размерных линий и угловые размеры при различных положениях углов наносят так, как показано на рис. 3. Если размерное число линейного или углового размера, наносимое над серединой размерной линии, попадает в заштрихованные зоны (в пределах угла 30°), то оно выносится на горизонтально расположенную полку линии-выноски. Для углов малых размеров при недостатке места размерные числа размещают на полках линий-выносок в любой зоне (угол 5° на рис. 3).


Рис.3
В случае необходимости нанесения размерного числа на заштрихованном поле изображения линии штриховки прерывают (рис. 3).

 Если для нанесения стрелок и размерных чисел недостаточно места, то их наносят одним из способов, показанных на рис. 4.
Если для нанесения стрелок и размерных чисел недостаточно места, то их наносят одним из способов, показанных на рис. 4.
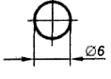


Рис. 4
При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки допускается заменять засечками, наносимыми под углом 45° к размерным линиям, или четко наносимыми точками (рис. 5).
|
|
|
 Рис. 5
Рис. 5
Перед размерным числом радиуса помещают прописную букву R (например, R 20), перед размерным числом диаметра — знак Ø(например, Ø20). При большой величине радиуса центр дуги окружности допускается приближать к дуге. В этом случае размерную линию радиуса показывают с изломом под углом 90° (рис. 6). Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать относительно центра (рис. 6). При проведении нескольких радиусов из одного центра размерные линии любых двух радиусов не располагают на одной прямой (рис. 7)
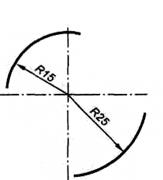

Рис. 6 Рис. 7

 Рис. 8 Рис. 9
Рис. 8 Рис. 9
Общее количество размеров на чертеже должно быть минимальным, но достаточным для изготовления и контроля изделия. Размеры одного и того же элемента на чертеже повторять не допускается. Размеры нескольких одинаковых элементов изделия, как правило, наносят один раз с указанием на полке линии-выноски или под ней количества этих элементов (рис. 8, рис. 9). При этом для элементов, равномерно расположенных по окружности (например, отверстий), угловые размеры между ними не ставят при условии, что один из этих элементов лежит на одной из осей симметрии. Наносится лишь размер диаметра окружности, на которой расположены центры отверстий (Ø 40 на рис. 8). Если ни одно из отверстий не лежит на оси симметрии, то следует задавать угол до первого элемента (рис. 9).
Глубина отверстий на чертежах показывается при разрезе детали. Поэтому и диаметры отверстий следует наносить преимущественно на соответствующих разрезах (рис. 10).
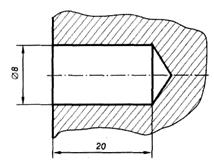
Рис. 10
Квадрат на чертеже определяют двумя размерами его сторон или одним размером со знаком □ (рис. 11). Диагонали, проведенные тонкими линиями, условно обозначают плоскость (ГОСТ 2.305-68).
|
|
|
 Размеры фасок под углом 45° и фасок под другими углами наносят, как показано на рис. 11
Размеры фасок под углом 45° и фасок под другими углами наносят, как показано на рис. 11
Рис. 11
На технических чертежах не допускается наносить размеры в виде замкнутой цепи, за исключением случая, когда один из них — справочный (размер 35* на рис. 11).
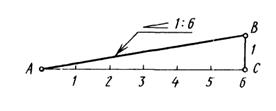 Уклон поверхности следует указывать непосредственно у изображения
Уклон поверхности следует указывать непосредственно у изображения
 Рис. 12
Рис. 12

 поверхности уклона или на полке – выноске в виде соотношения или в процентах (согласно ГОСТ 2.307-68). Уклон – это наклон одной линии относительно другой; измеряется отношением противолежащего катета к прилежащему. Перед размерным числом определяющим уклон, наносится знак
поверхности уклона или на полке – выноске в виде соотношения или в процентах (согласно ГОСТ 2.307-68). Уклон – это наклон одной линии относительно другой; измеряется отношением противолежащего катета к прилежащему. Перед размерным числом определяющим уклон, наносится знак  , острый угол которого должен быть направлен в сторону уклона (рис.12).
, острый угол которого должен быть направлен в сторону уклона (рис.12).
Рис.13
Конусность - это отношение диаметра конуса к его высоте. Если конус усеченный, то берется разность диаметров. K=D-d/H.
Как и уклон, конусность выражается отношением двух чисел или в процентах. Перед размерным числом, характеризующим конусность, наносят знак  , острый угол которого направлен в сторону вершины конуса (рис.12). Существуют следующие виды нормальных конусностей: 1:200, 1:100, 1:50, 1:30, 1:20, 1:15, 1:12,1:10, 1:8, 1:7, 1:5, 1:3 (если угол конусности меньше 28°). Если же угол – от 30 до 120°, то конусность обозначают на чертеже величиной угла.
, острый угол которого направлен в сторону вершины конуса (рис.12). Существуют следующие виды нормальных конусностей: 1:200, 1:100, 1:50, 1:30, 1:20, 1:15, 1:12,1:10, 1:8, 1:7, 1:5, 1:3 (если угол конусности меньше 28°). Если же угол – от 30 до 120°, то конусность обозначают на чертеже величиной угла.
Сопряжения линий
Сопряжением называется плавный переход от одной линии к другой, выполняемый с помощью сопрягающего элемента. Сопряжения часто встречаются в технических очертаниях. Поэтому построение сопряжения представляет большой практический интерес. Приемы построения сопряжения основаны на теоремах геометрии о прямых, касательных к окружности, и о взаимно касающихся окружностях.
Промежуточные дуги называют дугами сопряжения, их радиусы – радиусами сопряжения, центры – центрами сопряжения.
Построить сопряжение – значит найти центр сопряжения и точки сопряжения (точки касания линий).
Центр сопряжения - точка, равноудаленная от сопрягаемых линий. А общая для этих линий точка называется точкой сопряжения.
Построение сопряжений выполняется с помощью циркуля.
Возможны следующие виды сопряжения:
1) сопряжение пересекающихся прямых с помощью дуги заданного радиуса R (скругление углов);
2) сопряжение дуги окружности и прямой с помощью дуги заданного радиуса R;
3) сопряжение дуг окружностей радиусов R1и R2 прямой линией;
4) сопряжение дуг двух окружностей радиусов R1 и R2 дугой заданного радиуса R (внешнее, внутреннее и смешанное сопряжение)
|
|
|
При внешнем сопряжении центры сопрягаемых дуг радиусов R1 и R2 лежат вне сопрягающей дуги радиуса R. При внутреннем сопряжении центры сопрягаемых дуг лежат внутри сопрягающей дуги радиуса R. При смешанном сопряжении центр одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр другой сопрягаемой дуги - вне ее..
В табл. 1 показаны построения и даны краткие объяснения к построениям простых сопряжений.
Построение сопряжений
Таблица 1
| Пример простых сопряжений | Графическое построение сопряжений | Краткое объяснение к построению |
| 1. Сопряжение пересекающихся прямых с помощью дуги заданного радиуса R. | 
| Провести прямые, параллельные сторонам угла на расстоянии R. Из точки О взаимного пересечения этих прямых, опустив перпендикуляры на стороны угла, получим точки сопряжения 1 и 2. Радиусом R провести дугу. |
| 2. Сопряжение дуги окружности и прямой с помощью дуги заданного радиуса R. | 
| На расстоянии R провести прямую, параллельную заданной прямой, а из центра О1 радиусом R + R 1 — дугу окружности. Точка О — центр дуги сопряжения. Точку 2 получим на перпендикуляре, проведенном из точки О на заданную прямую, а точку 1 — на прямой OO 1. |
| 3. Сопряжение дуг двух окружностей радиусов R 1 и R 2 прямой линией. | 
| Из точки О1 провести окружность радиусом R1— R 2. Отрезок O1O2 разделить пополам и из точки О3 провести дугу радиусом 0,5 O 1 O 2. Соединить точки О1 и O2 с точкой А. Из точки О2 опустить перпендикуляр к прямой АО2, Точки 1.2 — точки сопряжения. |
| 4. Сопряжение дуг двух окружностей радиусов R 1 и R 2 дугой заданного радиуса R (внутреннее сопряжение). | 
| Из центров O 1 и О2 провести дуги радиусов R + R 1 и R + R 2. Получаем точку О — центр дуги сопряжения. Соединить точки O 1 и О2 с точкой О. Точки 1 и 2 являются точками сопряжения. |
| 5. Сопряжение дуг двух окружностей радиусов R 1 и R 2 дугой заданного радиуса R (внешнее сопряжение). | 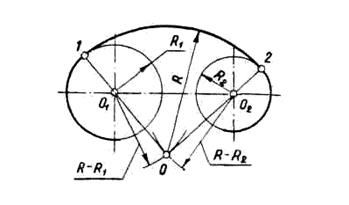
| Из центров O 1 и О2 провести дуги радиусов R — R 1 и R — R 2. Получаем точку О — центр дуги сопряжения. Соединить точки O 1 и О2с точкой О до пересечения с заданными окружностями. Точки 1 и 2 — точки сопряжения. |
| 6. Сопряжение дуг двух окружностей радиусов R 1 и R 2 дугой заданного радиуса R (смешанное сопряжение). | 
| Из центров O1 и О2 провести дуги радиусов R — R1 и R + R 2. Получаем точку О — центр дуги сопряжения. Соединить точки O 1 и О2 с точкой О до пересечения с заданными окружностями. Точки 1и 2 — точки сопряжения. |
Лекальные кривые
Это кривые линии, у которых на каждом их элементе непрерывно изменяется кривизна. Лекальные кривые не могут быть вычерчены с помощью циркуля, их построение выполняется по ряду точек. При вычерчивании кривой полученный ряд точек соединяют по лекалу, поэтому ее называют лекальной кривой линией. Точность построения лекальной кривой повышается с увеличением числа промежуточных точек на участке кривой.
К лекальным кривым относятся так называемые плоские сечения конуса – эллипс, парабола, гипербола, которые получаются в результате сечения кругового конуса плоскостью. Такие кривые рассматривались при изучении курса «Начертательная геометрия». К лекальным кривым также относят эвольвенту, синусоиду, спираль Архимеда, циклоидальные кривые.
Эллипс - геометрическое место точек, сумма расстояний которых до двух неподвижных точек (фокусов) есть величина постоянная.

Рис. 14
Наиболее широко применяется способ построения эллипса по заданным полуосям АВ и СD. При построении проводят две концентрические окружности, диаметры которых равны заданным осям эллипса. Для построения 12 точек эллипса окружности делят на 12 равных частей и полученные точки соединяют с центром.
На рис. 14 показано построение шести точек верхней половины эллипса; нижняя половина вычерчивается аналогично.
Эвольвента - является траекторией точки окружности, образованной ее развертыванием и выпрямлением (развертка окружности).
Построение эвольвенты по заданному диаметру окружности показано на рис. 15 Окружность делится на восемь равных частей. Из точек 1,2,3 проводят касательные к окружности, направленные в одну сторону. На последней касательной откладывают шаг эвольвенты, равный длине окружности
(2 pR), и полученный отрезок делят также на 8 равных частей. Откладывая на первой касательной одну часть, на второй – две части, на третьей – три части и т.д, получают точки эвольвенты.

Рис. 15
Циклоидальные кривые - плоские кривые линии, описываемые точкой, принадлежащей окружности, катящейся без скольжения по прямой линии или окружности. Если при этом окружность катится по прямой линии, то точка описывает кривую, называемую циклоидной.
Построение циклоиды по заданному диаметру окружности d показано на рис.16.
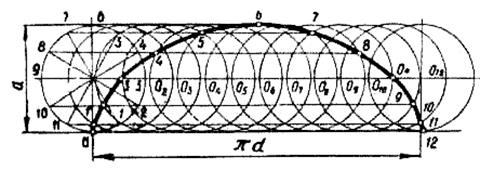 Рис. 16
Рис. 16
Окружность и отрезок длиной 2pR делят на 12 равных частей. Через центр окружности проводят прямую, параллельную отрезку. Из точек деления отрезка к прямой проводят перпендикуляры. В точках их пересечения с прямой получаем О1, О2, О3 и т.д. - центры перекатываемой окружности.
Из этих центров описываем дуги радиусом R. Через точки деления окружности проводим прямые параллельные прямой, соединяющей центры окружностей. На пересечении прямой, проходящей через точку 1 с дугой, описанной из центра О1, находится одна из точек циклоиды; через точку 2 с другой из центра О2 - другая точка и т.д.
Если же окружность катится по другой окружности, находясь внутри нее (по вогнутой части), то точка описывает кривую называемую гипоциклоидой. Если окружность катится по другой окружности, находясь вне ее (по выпуклой части), то точка описывает кривую, называемую эпициклоидой.
Построение гипоциклоиды и эпициклоиды аналогично, только вместо отрезка длиной 2pR берется дуга направляющей окружности.
Построение эпициклоиды по заданному радиусу подвижной и неподвижной окружностей показано на рис.17. Угол α, который вычисляется, и окружность радиуса R делят на восемь равных частей. Проводится дуга окружности радиуса R+r и из точек О1, О2, О3.. – окружности радиуса r.

Рис. 17
Построение гипоциклоиды по заданным радиусам подвижной и неподвижной окружности показано на рис.18. Угол α, который подсчитывается, и окружность радиуса R делятся на восемь равных частей. Проводится дуга окружности радиусом R - r и из точек О1, О2, О3… - окружности радиусом r.

Рис. 18
Парабола - это геометрическое место точек, равноудаленных от неподвижной точки - фокуса F и неподвижной прямой - директрисы, перпендикулярной к оси симметрии параболы. Построение параболы по заданному отрезку ОО =АВ и хорде СD показано на рис.19

Рис. 19
Прямые ОЕ и ОС разделены на одинаковое число равных частей. Дальнейшее построение ясно из чертежа.
 Гипербола - геометрическое место точек, разность расстояний которых от двух неподвижных точек (фокусов) - есть величина постоянная. Представляет собой две разомкнутые, симметрично расположенные ветви.
Гипербола - геометрическое место точек, разность расстояний которых от двух неподвижных точек (фокусов) - есть величина постоянная. Представляет собой две разомкнутые, симметрично расположенные ветви.
Рис. 20
Постоянные точки гиперболы F1 и F2- это фокусы, а расстояние между ними называется фокусным. Отрезки прямых, соединяющие точки кривой с фокусами, называются радиус-векторами. Гипербола имеет две взаимно перпендикулярные оси - действительную и мнимую. Прямые, проходящие через центр пересечения осей, называются асимптотами.
Построение гиперболы по заданному фокусному расстоянию F1F2 и углу α между асимптотами показано на рис.20. Проводится ось, на которой откладывается фокусное расстояние, которое делится пополам точкой О. Через точку О проводится окружность радиуса 0,5F1F2 до пересечения в точках C, D, E, K. Соединяя точки C с D и E c K, получают точки А и В – вершины гиперболы. От точки F1 влево отмечают произвольные точки 1, 2, 3… расстояния между которыми должны увеличиваться по мере удаления от фокуса. Из фокусных точек F1 и F2 радиусами R=B4 и r=A4 проводятся дуги до взаимного пересечения. Точки пересечения 4 являются точками гиперболы. Остальные точки строятся аналогично.
Синусоида - плоская кривая, выражающая закон изменения синуса угла в зависимости от изменения величины угла.
Построение синусоиды по заданному диаметру окружности d показано
 на рис. 21
на рис. 21
Рис. 21
Для ее построения делят данную окружность на 12 равных частей; на такое же число равных частей делится отрезок, равный длине данной окружности (2pR). Проводя через точки деления горизонтальные и вертикальные прямые, находят в пересечении их точки синусоиды.
Спираль Архимеда - э то плоская кривая, описываемая точкой, которая равномерно вращается вокруг заданного центра и вместе с тем равномерно удаляется от него.
Построение спирали Архимеда заданному диаметру окружности D показано на рис.22
Окружность и радиус окружности поделен на 12 равных частей. Дальнейшее построение видно из чертежа.
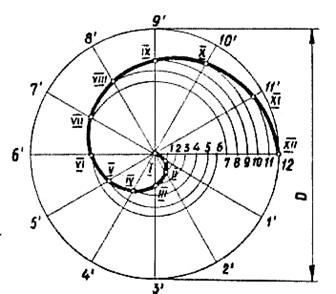
Рис. 22
При выполнении построении сопряжений и лекальных кривых приходится прибегать к простейшим геометрическим построениям - таким как деление окружности или прямой на несколько равных частей, деление угла и отрезка пополам, построение перпендикуляров, биссектрис и т.д. Все эти построения изучались в дисциплине «Черчение» школьного курса, поэтому подробно в данном пособии не рассматриваются.

 4. Методические указания по выполнению графической работы №1 «Геометрическое черчение»
4. Методические указания по выполнению графической работы №1 «Геометрическое черчение»
Задание выполняется на листе чертежной бумаги формата А3.
Содержание работы
1. Построить лекальную кривую.
2. Выполнить задание на построение сопряжений (рычаг).
3. Вычертить изображение детали «ролик» и проставить размеры.
Все задания индивидуальны и выбираются согласно своему варианту. Пример выполнения представлен в приложении на стр. 24
Порядок выполнения
1. Изучить ГОСТ 2.301-68 "Форматы", ГОСТ 2.303-68 "Линии", ГОСТ 2.307-68 "Нанесение размеров".
2. Ознакомиться с правилами построения уклона, конусности, сопряжений, лекальных кривых.
4. Выполнить рамку и основную надпись на чертеже.
5. Наметить места расположения заданий и надписей к ним.
6. Выполнить чертежи в тонких линиях, проставить размеры (шрифт 3,5), выполнить надписи (шрифт 5; 3,5). Построения выполняют чертежными инструментами при максимальной четкости и аккуратности.
7. После проверки чертежа преподавателем обвести линии
по ГОСТ 2.303-68 (0,8 - 1,00 мм).
8. Очистить поле чертежа от лишних линий и загрязнений (при этом вспомогательные построения следует сохранить).
|
|
|


