Работа и мощность тока. Закон Джоуля — Ленца в интегральной форме.

Электрическая энергия легко преобразуется в другие виды энергии — механическую, химическую, световую, внутреннюю энергию вещества, что широко применяется в промышленности и в быту. Мерой изменения энергии электрического тока служит работа источника тока, создающего и поддерживающего электрическое поле в цепи. Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения,

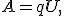
где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.

Учитывая, что q = It, где I — сила тока в проводнике, а t — время прохождения электрического тока, для работы тока получим

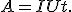
Если R — сопротивление однородного участка цепи, то, используя закон Ома для участка цепи, можно получить формулу для расчета работы тока:

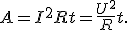
Если участок цепи не является однородным, то работу совершает не только стационарное электрическое поле, но и сторонние силы, и полная работа определяется по формуле

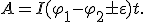
По вышеприведенным формулам можно рассчитать полную работу тока на данном участке цепи.

Если в цепи есть электродвигатель, то энергия электрического тока, во-первых, расходуется на совершение механической работы — полезная работа A _meh, во-вторых, затрачивается на нагревание обмоток электродвигателя и соединительных проводов — теряемая энергия. В этом случае коэффициент полезного действия можно рассчитать как

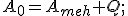
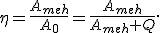
Говоря о коэффициенте полезного действия источника тока, под полезной работой подразумевают работу, совершаемую во внешней цепи постоянного тока:

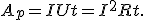
Затраченная же работа источника тока равна работе сторонних сил:

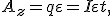
где .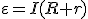

Тогда .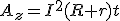

КПД источника 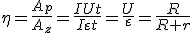, где U — напряжение во внешней цепи (напряжение на полюсах источника тока). Графическая зависимость η = f (R) при r = const приведена на рис. 1.

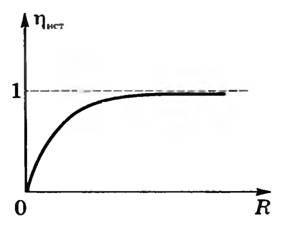
Рис. 1

Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж.

1 Дж = Кл·В = А·В·с.

Измеряют работу электрического тока счетчиками.

Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле 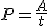или P = IU.

Используя закон Ома для участка цепи, можно записать иначе формулу для мощности тока: 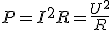. В этом случае речь идет о тепловой мощности.

Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.

Кроме того, применяют внесистемные единицы: киловатт-час или гектоватт-час: 1 кВт·ч = 3,6·10⁶ Дж = 3,6 МДж; 1 гВт·ч = 3,6·10⁵ Дж = 360 кДж.

Для измерения мощности тока существуют специальные приборы — ваттметры.

Рассмотрим однородный проводник, к кон­цам которого приложено напряжение U. За время At через сечение проводника перено­сится заряд dq = Idt. Так как ток пред­ставляет собой перемещение заряда dq под действием электрического поля, то, по формуле (84.6), работа тока

dA=Udq=IUdt. (1)

Если сопротивление проводника R, то, ис­пользуя закон Ома (1), получим

dA=I²Rdt=(U ² /r)dt. (2)

Из (99.1) и (99.2) следует, что мощ­ность тока

P=dA/dt=UI=I²R=U²/R. (3)

Если сила тока выражается в амперах, напряжение — в вольтах, сопротивле­ние — в омах, то работа тока выражается в джоулях, а мощность — в ваттах. На практике применяются также внесистем­ные единицы работы тока: ватт-час (Вт•ч) и киловатт-час (кВт•ч). 1 Вт•ч — работа тока мощностью в 1 Вт в течение 1 ч: 1 Вт•ч = 3600 Вт•с = 3,6•10³ Дж; 1 кВт•ч=10³ Вт•ч = 3,6•10⁶ Дж.

Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,

dQ=dA. (4)

Таким образом, используя выражения (4), (1) и (.2), получим

Выражение (5) представляет собой за­кон Джоуля — Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.

Выделим в проводнике элементарный цилиндрический объем dV=dSd l (ось ци­линдра совпадает с направлением тока),

сопротивление которого R= r(d l /dS). По закону Джоуля — Ленца, за время d t в этом объеме выделится теплота

Количество теплоты, выделяющееся за единицу времени в единице объема, на­зывается удельной тепловой мощностью тока. Она равна

w=rj². (6)

Используя дифференциальную форму за­кона Ома (j =gE) и соотношение r=1/g, получим

w = jE =g E ². (7)

Формулы (6) и (7) являются обоб­щенным выражением закона Джоуля — Ленца в дифференциальной форме, при­годным для любого проводника.

Тепловое действие тока находит широ­кое применение в технике, которое нача­лось с открытия в 1873 г. русским инжене­ром А. Н. Лодыгиным (1847—1923) лам­пы накаливания. На нагревании, про­водников электрическим током основано действие электрических муфельных печей, электрической дуги (открыта русским ин­женером В. В. Петровым (1761 — 1834)), контактной электросварки, бытовых элек­тронагревательных приборов и т. д.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов 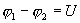, тогда работу по переносу заряда q на этом участке равна 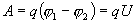По определению I= q/t. откуда q= I t. Следовательно 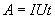Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

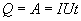(17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: