Остаточный член формулы Тейлора

Формула Тейлора

Теорема 8 (теорема Тейлора). Пусть функция f (x) имеет в точке x = a и некоторой ее окрестности производные порядка n+ 1. Тогда между точками a и x ¹ a найдется такая точка , что справедлива следующая формула:

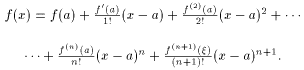
(10)

Формула (10) называется формулой Тейлора, а выражение

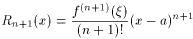
представляет остаточный член в форме Лагранжа. Заметим, что если функция f (n+ 1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x ® a более высокого порядка, чем (x-a) ⁿ. Таким образом, остаточный член можно записать в виде

R_n+ 1(x) = o ((x-a) ⁿ) при x ® a.

Данная форма записи остаточного члена называется формой Пеано.

Формулой Маклорена называется формула Тейлора при a = 0:

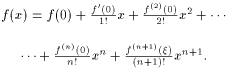
(11)

Остаточный член в форме Пеано для формулы Маклорена имеет вид

R_n+ 1 = o (xⁿ) при x ® 0.

Приведем разложения некоторых элементарных функций по формуле Маклорена

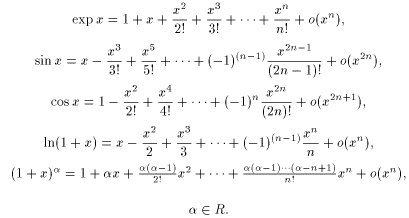
Формула Тейлора для многочленов и функций. Разложение в ряд Тейлора

Начнем изучение формулы Тейлора на примере многочленов. Пусть у нас есть многочлен 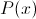степени m, также мы знаем значение данного многочлена в некоторой точке 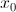и знаем значение первых m производных многочлена 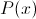, тогда мы можем представить наш многочлен в следующем виде:

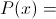
Если же к примеру нам известны значения первых n < m производных многочлена 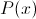, то исходный многочлен мы можем представить в виде:

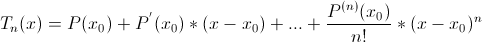- это и есть формула Тейлора степени n для многочлена 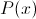. Т.е. представление многочлена по степеням 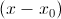с коэффициентами представимих через производные данного многочлена. Наш многочлен представим в ви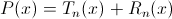де , где 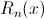остаточный членформулы Тейлора.

Способы разложения в ряд Тейлора:

Из вида формулы Тейлора сразу же приходит в голову один из способов: посчитать необходимое количество производных и найти их значения в соответствующей точке.

Разложить в ряд Тейлора используя разложения элементарных функций(разложение элементарных функций мы приведем в следующей статье). Этот способ требует своеобразной смекалки, знания разложений элементарных функций.

Остаточный член формулы Тейлора

Остаточный член формулы Тейлора может быть представлен в форме Лагранжа, Коши или Пеано. Остановимся на каждом из представлений немного подробнее.

1) - остаточный член в форме Лагранжа.

2) - остаточный член в форме Коши.

3) 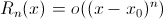- остаточный член в форме Пеано,

где с - точка из интервала 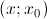либо интервала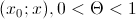

Формула Тейлора применяется при приближенном подсчете значения функции в какой-либо точке, а остаточный член посчитанный в этой точке показывает погрешность вычислений. Формулу Тейлора разложенную в окрестности нуля, т.е. когда <.noindex> называют формулой Маклорена.

Многочлен Тейлора

Многочлен , наиболее подходящий (с некоторой точки зрения) для этой цели, называется многочленом Тейлора для данной функции; найдя его по заданной функции , мы сможем вместо сложного вычисления значений функции приближённо заменять это вычисление на вычисление значений многочлена¹⁶ .

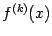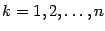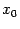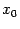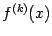Уточним теперь постановку задачи. Пусть функция определена в некоторой окрестности некоторой точки и имеет всюду в окрестности производные при . Многочленом Тейлора степени в точке называется такой многочлен степени , такой, что его значение и значение всех его производных, вычисленные в точке , равны соответствующим значениям функции и её производных до порядка в этой же точке:

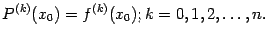
Если это условие совпадения выполнено, то графики функций и 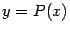, по крайней мере при 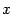, близких к 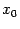, будут идти весьма тесно друг к другу. Равенство

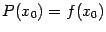
означает, что графики проходят через одну и ту же точку 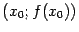; равенство

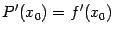
означает, что эти графики имеют в этой общей точке совпадающие касательные (так как общее значение производной -- это общий угловой коэффициент касательной); равенство

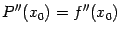
означает, как мы убедимся ниже, что эти графики имеют в общей точке одинаковую кривизну, и т. д.

Для нахождения вида многочлена Тейлора для заданной функции сделаем сначала следующее замечание. Любой многочлен степени вида

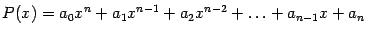
можно представить в виде, расположенном по степеням бинома :

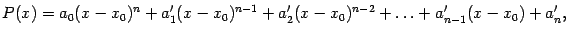
и наоборот, раскрыв скобки в последней формуле, мы можем получить многочлен по степеням .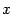

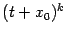Действительно, положив , мы можем подставить в правую часть формулы , раскрыть степени при 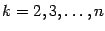по формуле бинома Ньютона, а потом привести подобные члены. Все коэффициенты 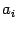(кроме 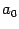) и свободный член при этом изменятся на некоторые другие ( 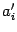в нашей формуле), но получится многочлен по степеням бинома 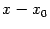, имеющий ту же степень .

Итак, будем предполагать, что многочлен Тейлора мы ищем в виде

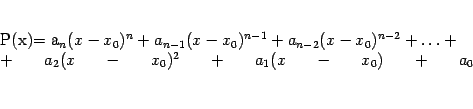
при некоторых коэффициентах 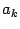, пока не известных. Отыщем значения этих коэффициентов Тейлора по значениям производных данной функции в точке .

Учтём требование к значению многочлена: 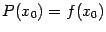. Подставив в равенство (Тейлор 1) 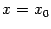, получим, что , так как все остальные слагаемые обратятся в 0. Тем самым

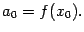
Учтём затем требование к значению первой производной многочлена: . Производная от равна

Подставив в равенство (Тейлор 2) значение 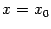, получим, что 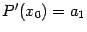, так как снова все остальные слагаемые обратятся в 0. Отсюда

Следующее требование -- к значению второй производной многочлена: 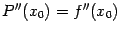. Вторая производная от равна

Снова подставив в равенство (Тейлор 3) значение 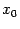, получим, что , откуда

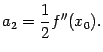
Далее нетрудно сообразить, что получится 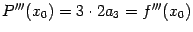, откуда

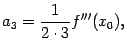
и вообще,

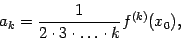
при . Учитывая, что 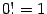, , , ,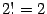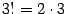..., последнюю формулу можно записать в виде

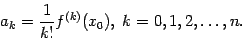
Итак, мы получили, что многочлен Тейлора для функции в точке 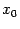имеет вид

 

Поделиться:

Воспользуйтесь поиском по сайту: