 |
Синхронные счётчики.
|
|
|
|
В рассмотренных схемах делителей частоты быстродействие всей схемы определяется временем распространения сигнала от входа до выхода самого старшего разряда. При этом получается, что чем больше требуемый коэффициент деления, тем больше двоичных разрядов счётчика требуется для реализации этого делителя. Тем большее время требуется для распространения сигнала от входа синхронизации счётчика, до его выхода, и тем меньше будет предельная частота, которую можно подавать на вход этого делителя.
Первая схема, которую мы рассмотрим - это схема кольцевого счётчика. Такой счётчик можно построить на основе сдвигового регистра. Схема кольцевого счётчика приведена на рисунке 13.4.

Рисунок 13.4 Схема кольцевого счетчика.
Рассмотрим работу этой схемы. Пусть первоначально в счетчике записано число 002. После первого же тактового импульса состояние счётчика станет равным 102, после второго - 112. Временные диаграммы этой схемы приведены на рисунке 13.5.

13.5 - Временные диаграммы к кольцевому счетчику.
В результате анализа временных диаграмм можно определить, что коэффициент деления схемы кольцевого счётчика будет равен: Кд = 2*n.
Для того чтобы избежать неправильной работы счётчика в этот счётчик можно ввести схему контроля правильной работы. В простейшем случае это может быть обычный логический элемент “И-НЕ”. Этот элемент будет контролировать состояние счётчика, соответствующее единицам во всех его разрядах. Схема 2-разрядного счётчика со схемой проверки правильности его работы приведена на рисунке 13.6.

Рисунок 13.6 - Схема 2-разрядного счетчика с проверкой правильности его работы.
В этой схеме триггеры счётчика при поступлении импульсов на тактовый вход последовательно заполняются единицами. Как только все триггеры будут заполнены единицами, на выходе логического элемента “2И-НЕ” появится уровень логического нуля. При поступлении следующего тактового импульса этот ноль будет записан в первый триггер счётчика. В дальнейшем работа счётчика повторяется. Временные диаграммы сигналов на выходах этого счётчика приведены на рисунке 13.7.
|
|
|

Рисунок 13.7 – Временные диаграммы.
Дешифратор - преобразователь кодов, выполняющий преобразование входных двоичных кодов в выходной унитарный код. Унитарный код двоичного n – разрядного числа представляется 2n разрядами, только один из разрядов которого равен 1 (или 0). Условное описание дешифратора задаётся формулой nxm (n на m), для полного дешифратора это формула nx2n. Примерами полных являются дешифраторы: 1x2, 2x4, 3x8, 4x16.
Рассмотрим пример. Составим таблицу, в которой каждому выходному сигналу сопоставляется последовательность из двух входных сигналов.

Рисунок 9.1 – Таблица истинности
На основании данной таблицы истинности составим формулу для функций A, B, C и D:

На основании полученных функций построим логическую схему. Схема должна иметь два входа и четыре выхода.

Рисунок 9.2 – Логическая схема дешифратора
Мультиплексор
Мультиплексором называется комбинационная схема, имеющая m+2m входов и один выход, где m – количество адресных входов, а 2m – количество информационных входов мультиплексора. Адреса представляются в двоичном коде и им присваивается номер j. Каждому адресу с номером j соответствует свой информационный вход Aj, сигнал с которого при данном адресе проходит на выход. Основным назначением мультиплексора является коммутация 2m входных сигналов на один выход. Таким образом, мультиплексор выполняет функцию

где X – двоичный код адреса; Aj – входные информационные сигналы мультиплексора; Kj(X) – конституенты 1, принимающие значения, равные 1 на единственном наборе переменных X = j. Условное описание мультиплексора задаётся формулой 2mx1. Примерами являются мультиплексоры: 2x1, 4x1, 8x1, 16x1.
|
|
|
В состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 10.1. Это позволяет управлять переключением информационных входов при помощи двоичных кодов, подаваемых на управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.

Рисунок 10.1 – Схема подключения мультиплексора с дешифратором
Условно графическое обозначение четырёхвходового мультиплексора с двоичным управлением приведено на рисунке 10.2. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Сами входные сигналы обозначены как X0, X1, X2 и X3.

Рисунок 10.2 - Четырёхвходовой мультиплексор
Демультиплексор
Демультиплексорами называются устройства, которые позволяют подключать один вход к нескольким выходам. Демультиплексор можно построить на основе точно таких же схем логического "И", как и при построении мультиплексора. Существенным отличием от мультиплексора является возможность объединения нескольких входов в один без дополнительных схем. Однако для увеличения нагрузочной способности микросхемы, на входе демультиплексора для усиления входного сигнала лучше поставить инвертор.
Схема демультиплексора приведена на рисунке 1.1. В этой схеме для выбора конкретного выхода демультиплексора, как и в мультиплексоре, используется двоичный дешифратор.

Рисунок 11.1 – Схема демультиплексора
Однако, если рассмотреть принципиальную схему самого дешифратора, то можно значительно упростить демультиплексор. Достаточно просто к каждому логическому элементу 'И', входящему в состав дешифратора просто добавить ещё один вход – In. Такую схему часто называют дешифратором с входом разрешения работы. Условно-графическое изображение демультиплексора приведено на рисунке 11.2.

Рисунок 11.2 Условно графическое обозначение демультиплексора с четырьмя выходами.
В этом обозначении вход In обозначен как вход E, а выходы не названы никак, оставлены только их номера.
|
|
|
Сумматор
Сумматор - логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учет знаков чисел, выравнивание порядков слагаемых и тому подобное.
Сумматоры классифицируются по разным признакам:
1. В зависимости от системы исчисления:
Двоичные
Двоично-десятичные (двоично кодированые)
Десятичные
Прочие (пример: амплитудные)
2. По количеству одновременно обрабатываемых разрядов складываемых чисел:
Одноразрядные
Многоразрядные
3. По числу входов и выходов одноразрядных двоичных сумматоров:
Четвертьсумматоры, характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
Полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом ≈ перенос в следующий (более старший разряд);
Полные одноразрядные двоичные сумматоры, характеризующиеся наличием трех входов, на которые подаются одноименные разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом ≈ перенос в следующий (более старший разряд).
4. По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:
Последовательные, в которых обработка чисел ведется поочередно, разряд за разрядом, на одном и том же оборудовании;
Параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется свое оборудование.
Построение двоичных сумматоров обычно начинается с сумматора по модулю 2. На рисунке 14.1 приведена таблица истинности этого сумматора. Ее можно получить исходя из правил суммирования в двоичной арифметике.
|
|
|

Рисунок 14.1 – Таблица истинности сумматора по модулю 2.

Схема сумматора по модулю 2 приведена на рисунке 14.2.
Рисунок 14.2 - Принципиальная схема, реализующая таблицу истинности сумматора по модулю 2.
Сумматор по модулю 2 (для двоичной арифметики его схема совпадает со схемой исключающего "ИЛИ") изображается на схемах как показано на рисунке 14.3.

Рисунок 14.3. Изображение схемы, выполняющей логическую функцию исключающего "ИЛИ".
Сумматор по модулю 2 выполняет суммирование без учета переноса. В полном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена на рисунке 14.4.

Рисунок 14.4 - Таблица истинности полусумматора.
Принципиальная схема, реализующая таблицу истинности полусумматора представлена на рисунке 14.5. Полусумматор изображается на схемах как показано на рисунке 14.6.
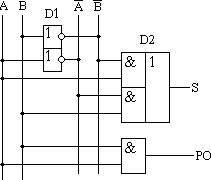
Рисунок 14.5 - Принципиальная схема, реализующая таблицу истинности полусумматора.

Рисунок 14.6 - Изображение полусумматора на схемах.
Схема полусумматора формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому она и называется полусумматором. Таблицу истинности полного двоичного одноразрядного сумматора можно получить из правил суммирования двоичных чисел. Она приведена на рисунке 14.7. В обозначении входов использовано следующее правило: в качестве входов использованы одноразрядные числа A и B; перенос обозначен буквой P; для обозначения входа переноса используется буква I (сокращение от английского слова input – вход); для обозначения выхода переноса используется буква O (сокращение от английского слова output – выход).
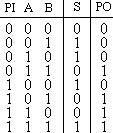
Рисунок 14.7 - Таблица истинности полного двоичного одноразрядного сумматора.
По таблице 14.7 составим схему полного двоичного одноразрядного сумматора. Эта схема приведена на рисунке 14.8. Ее можно минимизировать, но это несколько усложняет принципы построения сумматоров, поэтому вопросы минимизации рассматриваться не будут.
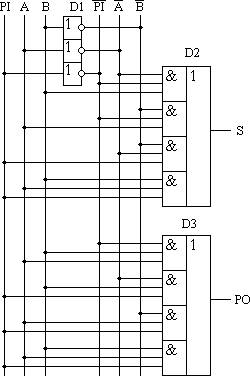
Рисунок 14.8. Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора.
Полный двоичный одноразрядный сумматор изображается на схемах как показано на рисунке 14.9.

Рисунок 14.9 Изображение полного двоичного одноразрядного сумматора на схемах.
Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов.
|
|
|


