 |
Тестовые задания 1 рубежного контроля по дисциплине «биостатистика» для студентов 3 курса по специальностям «Медико-профилактическое дело» и «Сестринское дело»
|
|
|
|
1. ~Общественная наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи их с качественной стороной:
|статистика
|математика
|обществоведение
|динамика
|кибернетика
2. ~Статистика – это наука, которая изучает:
|социальные закономерности здоровья людей
|деятельность лечебно-профилактических учреждений
|действие законов рынка в системе медицинской помощи
|количественную сторону массовых явлений в неразрывной связи с их качественной стороной
|законы распределения болезней среди разных социальных прослоек населения и причины этого распределения
3. ~Статистика как самостоятельная наука начала формироваться в... веке.
|XVII
|XVI
|XVIII
|XIX
|XX
4. ~Статистика, изучающая вопросы, связанные с биологией, медициной, фармацией, гигиеной и здравоохранением, называется:
|математикой
|биостатистикой
|обществоведением
|динамикой
|кибернетикой
5. ~Биостатистика – это:
|статистика, изучающая действие законов рынка в системе медицинской помощи
|совокупность методов, которые обеспечивают сбор, хранение и анализ медицинской информации
|медицинская и статистическая информация о законах распределения болезней среди разных социальных прослоек населения
|статистика, изучающая вопросы, связанные с биологией, медициной, фармацией, гигиеной и здравоохранением
|наука, которая изучает деятельность лечебно-профилактических учреждений
6. ~Биостатистика относится к:
|политической статистике
|экономической статистике
|социальной статистике
|статистике науки
|статистике образования
7. ~Термин «биометрия» ввел:
|Р. Фишер
|Ф. Гальтон
|К. Пирсон
|А. Кетле
|В. Уэлдон
8. ~Основы биометрии начинаются с:
|
|
|
|Ф. Гальтона
|Р. Фишера
|К. Пирсона
|А. Кетле
|В. Уэлдона
9. ~Английский ученый, который ввел в биометрию понятие стандартного отклонения и коэффициента вариации, разработал основы множественной регрессии, нелинейной корреляции и регрессии, теорию сопряженности признаков:
|Р. Фишер
|Ф. Гальтон
|К. Пирсон
|А. Кетле
|В. Уэлдон
10. ~Английский зоолог, биометрик, первый организатор журнала «Биометрика»:
|А. Кетле
|В. Уэлдон
|К. Пирсон
|Р. Фишер
|Ф. Гальтон
11. ~Английский ученый, основоположник теории выборочных распределений, методов дисперсионного и дискриминантного анализа, теории планирования эксперимента, метода максимального подобия:
|Ф. Гальтон
|К. Пирсон
|Р. Фишер
|А. Кетле
|В. Уэлдон
12. ~Первый этап статистического исследования - … данных.
|анализ
|публикация
|сбор
|представление
|обработка
13. ~... данных - процесс получения информации об элементах исследуемой совокупности и их свойствах.
|Анализ
|Представление
|Сбор
|Публикация
|Обработка
14. ~К количественным данным не относятся:
|дискретные
|дихотомические
|непрерывные
|интервальные
|относительные
15. ~К количественным данным не относятся:
|бинарные
|дискретные
|непрерывные
|интервальные
|относительные
16. ~К количественным данным не относятся:
|дискретные
|номинальные
|непрерывные
|интервальные
|относительные
17. ~К количественным данным не относятся:
|дискретные
|непрерывные
|порядковые
|интервальные
|относительные
18. ~К качественным данным не относятся:
|дискретные
|номинальные
|порядковые
|дихотомические
|ранги
19. ~К качественным данным не относятся:
|непрерывные
|номинальные
|порядковые
|дихотомические
|ранги
20. ~К качественным данным не относятся:
|интервальные
|номинальные
|порядковые
|дихотомические
|ранги
21. ~К качественным данным не относятся:
|номинальные
|порядковые
|
|
|
|относительные
|дихотомические
|ранги
22. ~Количественные данные, которые представлены только в виде целого числа, т.е. не могут иметь дробную часть:
|дискретные
|номинальные
|порядковые
|дихотомические
|ранги
23. ~Количественные данные, которые получают при измерении на непрерывной шкале, т.е. теоретически они могут иметь дробную часть:
|номинальные
|порядковые
|дихотомические
|непрерывные
|дискретные
24. ~Вид непрерывных данных, которые измеряются в абсолютных величинах, имеющих физический смысл:
|интервальные
|номинальные
|порядковые
|дихотомические
|дискретные
25. ~Вид непрерывных данных, отражающих долю значения признака по отношению к исходному значению этого признака:
|относительные
|номинальные
|порядковые
|дихотомические
|дискретные
26. ~Качественные данные, которые отражают условные коды неизмеряемых категорий:
|дискретные
|номинальные
|порядковые
|дихотомические
|ранги
27. ~Качественные данные, которые отражают условную степень выраженности какого-либо признака:
|номинальные
|порядковые
|дискретные
|дихотомические
|ранги
28. ~Качественные данные, которые имееют лишь два возможных значения какого-либо признака:
|номинальные
|дихотомические
|дискретные
|порядковые
|ранги
29. ~График, в котором статистические данные изображаются различными геометрическими фигурами:
|картограмма
|картодиаграмма
|диаграмма
|график «ящик с усами»
|график «стебель и листья»
30. ~Диаграмма, изображающая динамику явления, называется:
|столбиковой
|линейной
|внутристолбиковой
|секторной
|радиальной
31. ~Диаграммы, изображающие динамику или статику явления в соответствии с избранным масштабом:
|линейные
|столбиковые
|внутристолбиковые
|секторные
|радиальные
32. ~График, представленый на рисунке:

|график «ящик с усами»
|график «стебель и листья»
|линейная диаграмма
|внутристолбиковая диаграмма
|секторная диаграмма
33. ~Вид линейной диаграммы, применяемой для изображения динамики явления за замкнутый цикл времени (сутки, неделя, месяц, год):
|внутристолбиковая
|радиальная
|столбиковая
|линейная
|секторная
34. ~Диаграмма, представленная на рисунке:

|внутристолбиковая
|радиальная
|
|
|
|объемная
|линейная
|секторная
35. ~Диаграммы, отражающие структуру явления, выраженного экстенсивными показателями, и представляющие собой прямоугольник, в котором цветом выделены составляющие его части в соответствии с их удельным весом:
|столбиковые
|линейные
|внутристолбиковые
|секторные
|радиальные
36. ~График, который представляет собой смесь диаграммы и таблицы, эффективен для отображения данных по увеличению порядка величины:
|линейная диаграмма
|внутристолбиковая диаграмма
|график «стебель и листья»
|секторная диаграмма
|график «ящик с усами»
37. ~График, представленый на рисунке:

|столбиковый
|линейный
|внутристолбиковый
|секторный
|радиальный
38. ~График, представленый на рисунке:
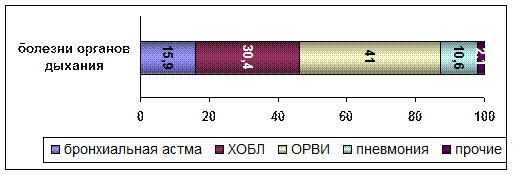
|столбиковый
|линейный
|внутристолбиковый
|секторный
|радиальный
39. ~График, представленный на рисунке:
| 1,0 | ||
| 1,1 | ||
| 1,2 | ||
| 1,3 | ||
| 1,4 | ||
| 1,5 | ||
| 1,6 | ||
| 1,7 | ||
| 1,8 | ||
| 1,9 | ||
| 2,0 | ||
| 2,1 | ||
| 2,2 |
|линейная диаграмма
|внутристолбиковая диаграмма
|график «стебель и листья»
|секторная диаграмма
|график «ящик с усами»
40. ~Необходимый, обязательный элемент измерительной процедуры:
|диаграмма
|таблица
|шкала
|гистограмма
|рисунок
41. ~График, представленый на рисунке:
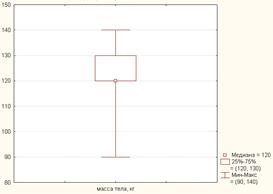
|график «стебель и листья»
|столбиковая диаграмма
|внутристолбиковая диаграмма
|график «ящик с усами»
|секторная диаграмма
42. ~Процедура сравнения объектов по определенным показателям или характеристикам:
|построение диаграммы
|определение коэффициента
|измерение
|создание таблиц
|изображение
43. ~Шкала, используемая для классификации свойств объекта:
|порядковая
|интервальная
|номинальная
|отношений
|ранговая
44. ~Номинальная шкала:
|упорядочивает значения признака
|показывает размах отдельных измерений
|используется для классификации свойств объекта
|выявляет соотношение измеренных значений
|используется для изменения формы объекта
45. ~Пол, национальность, цвет глаз и волос, диагноз пациента измеряются шкалой:
|
|
|
|порядковой
|интервальной
|номинальной
|отношений
|ранговой
46. ~Значения признака упорядочивает шкалой:
|порядковая
|интервальная
|отношений
|номинальная
|наименований
47. ~Стадии гипертонической болезни и степени сердечной недостаточности измеряются шкалой:
|номинальной
|порядковой
|интервальной
|отношений
|наименований
48. ~Порядковая шкала:
|используется для классификации свойств объекта
|показывает размах отдельных измерений
|упорядочивает значения признака
|выявляет соотношение измеренных значений
|используется для изменения формы объекта
49. ~ «Размах» отдельных измерений признака показывает … шкала.
|отношений
|интервальная
|номинальная
|порядковая
|наименований
50. ~Интервальная шкала:
|используется для классификации свойств объекта
|упорядочивает значения признака
|показывает размах отдельных измерений
|выявляет соотношение измеренных значений
|используется для изменения формы объекта
51. ~Время, температура, тестовые баллы измеряются шкалой:
|номинальной
|интервальной
|порядковой
|отношений
|ранговой
52. ~Соотношение измеренных значений признака выявляет:
|номинальная шкала
|шкала отношений
|порядковая шкала
|интервальная шкала
|шкала наименований
53. ~Рост, вес, время реакции, количество выполненных заданий теста измеряются:
|интервальной шкалой
|номинальной шкалой
|шкалой отношений
|порядковой шкалой
|ранговой шкалой
54. ~Шкала отношений:
|выявляет соотношение измеренных значений
|используется для классификации свойств объекта
|упорядочивает значения признака
|показывает размах отдельных измерений
|используется для изменения формы объекта
55. ~Измерение должно быть:
|надежным и достоверным
|адекватным и актуальным
|условным и несмещенным
|значимым и обоснованным
|правильным и своевременным
56. ~Распределение случайной величины, представленое на графике:

|показательное
|нормальное
|равномерное
|геометрическое
|биномиальное
57. ~Нормальный закон распределения – это закон:
|Гаусса
|Пуассона
|Бернулли
|Ляпунова
|Чебышева
58. ~В медико-биологических исследованиях наиболее часто встречается распределение:
|нормальное
|биноминальное
|Пуассона
|равномерное
|геометрическое
59. ~Статистическая совокупность - это:
|совокупность элементов, которая состоит из бесконечно большого числа элементов
|каждый частный случай явления, которое изучается
|совокупность однородных по какому-либо признаку объектов, ограниченных пространством и временем
|часть генеральной совокупности элементов, которая охватывается наблюдением
|
|
|
|общее число элементов наблюдения
60. ~Cовокупность однородных по какому-либо признаку объектов, ограниченных пространством и временем называется:
|генеральной совокупностью
|выборочной совокупностью
|статистической совокупностью
|объемом выборки
|элементом наблюдения
61. ~В статистике свойство объектов или явлений, которое может быть наблюдаемо или измерено:
|показатель
|особенность
|признак
|результат
|характеристика
62. ~Если невозможно провести сплошное наблюдение, то используют метод:
|одиночный
|равномерный
|нормальный
|показательный
|выборочный
63. ~Метод статистического обследования, при котором из статистической совокупности выбирают ограниченное число объектов и их подвергают изучению, называется:
|одиночным
|равномерным
|выборочным
|нормальным
|показательным
64. ~Генеральная статистическая совокупность – это:
|каждый частный случай явления, которое изучается
|критерий, который характеризует единицу наблюдения
|часть генеральной совокупности элементов, которая охватывается наблюдением
|совокупность элементов, которая состоит из бесконечно большого числа элементов
|общее число элементов наблюдения
65. ~Совокупность элементов, которая состоит из бесконечно большого числа элементов, называется:
|статистической совокупностью
|выборочной совокупностью
|генеральной совокупностью
|объемом выборки
|элементом наблюдения
66. ~Выборочная совокупность – это:
|совокупность элементов, которая состоит из бесконечно большого числа элементов
|каждый частный случай явления, которое изучается
|часть генеральной совокупности элементов, которая охватывается наблюдением
|критерий, который характеризует единицу наблюдения
|общее число элементов наблюдения
67. ~Часть генеральной совокупности элементов, которая охватывается наблюдением называется:
|генеральной совокупностью
|статистической совокупностью
|объемом выборки
|выборочной совокупностью
|элементом наблюдения
68. ~Объем выборки – это:
|часть генеральной совокупности элементов, которая охватывается наблюдением
|совокупность элементов, которая состоит из бесконечно большого числа элементов
|каждый частный случай явления, которое изучается
|общее число элементов наблюдения
|критерий, который характеризует единицу наблюдения
69. ~Общее число элементов наблюдения называется:
|выборочной совокупностью
|генеральной совокупностью
|статистической совокупностью
|объемом выборки
|элементом наблюдения
70. ~Элемент наблюдения – это:
|каждый частный случай явления, которое изучается
|общее число элементов наблюдения
|часть генеральной совокупности элементов, которая охватывается наблюдением
|совокупность элементов, которая состоит из бесконечно большого числа элементов
|критерий, который характеризует единицу наблюдения
71. ~Каждый частный случай явления, которое изучается называется:
|элементом наблюдения
|объемом выборки
|выборочной совокупностью
|генеральной совокупностью
|статистической совокупностью
72. ~Объем малой выборки:
| n ≤30
| n ≤50
| n ≤60
| n ≤100
| n ≤200
73. ~Значения варьирующего признака:
|частоты
|децили
|варианты
|доли
|квантили
74. ~Числа, показывающие сколько раз встречается каждый вариант, называются:
|вариантами
|децилями
|долями
|частотами
|квантилями
75. ~Упорядоченная выборка называется:
|законом распределения
|полигоном
|вариационным рядом
|гистограммой
|вариантом
76. ~Вариационный ряд представляется в виде:
|диаграммы
|таблицы
|шкалы
|числа
|формулы
77. ~Виды вариационных рядов:
|качественные, количественные
|полные, частичные
|дискретные, интервальные
|точные, неопределенные
|случайные, определенные
78. ~График, представляющий собой ломаную, соединяющую точки «xi», «νi» (xi - варианты признака, νi - частоты):
|гистограмма
|полигон
|радиальная диаграмма
|внутристолбиковая диаграмма
|секторная диаграмма
79. ~График, представленный на рисунке:

|гистограмма
|радиальная диаграмма
|полигон
|внутристолбиковая диаграмма
|секторная диаграмма
80. ~Формула Стерджеса применяется для определения числа:
| интервалов
| частот
| наблюдений
| признаков
| вариант
81. ~Формула Стерджеса:
| k =1-3,322lg n
| k =1+3,322lg n
| k =2+3,322lg n
| k =2-3,322lg n
| k =3+3,322lg n
82. ~Величина интервала определяется по формуле:
| 
| 
| 
| 
| 
83. ~График, представленный на рисунке:

|секторная диаграмма
|радиальная диаграмма
|внутристолбиковая диаграмма
|гистограмма
|полигон
84. ~Ступенчатая фигура, используемая для представления интервального вариационного ряда:
|полигон
|радиальная диаграмма
|гистограмма
|секторная диаграмма
|линейная диаграмма
85. ~Вариационный ряд характеризуется показателями:
|дискретными и интервальными
|полными и частичными
|центральной тенденции и разнообразия
|случайными и определенными
|качественными и количественными
86. ~Показатели центральной тенденции:
|абсолютные и относительные величины
|простые и взвешенные величины
|полигон и гистограмма
|варианты и частоты
|средние и структурные величины
87. ~Формула средней арифметической простой:
| 
| 
| 
| 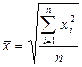
| 
88. ~  - средняя … величина.
- средняя … величина.
|арифметическая взвешенная
|геометрическая простая
|арифметическая простая
|квадратическая простая
|квадратическая взвешенная
89. ~Формула средней арифметической взвешенной:
| 
| 
| 
| 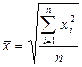
| 
90. ~  - средняя … величина.
- средняя … величина.
|арифметическая простая
|геометрическая простая
|арифметическая взвешенная
|квадратическая простая
|квадратическая взвешенная
91. ~Варианта, находящаяся в середине ряда:
|мода
|медиана
|дисперсия
|среднее квадратическое отклонение
|среднее арифметическое значение
92. ~Медиана - это варианта:
|с наибольшей частотой
|находящаяся в середине ряда
|с наименьшей частотой
|находящаяся в начале ряда
|находящаяся в конце ряда
93. ~Мода - это варианта:
|с наименьшей частотой
|с наибольшей частотой
|находящаяся в середине ряда
|находящаяся в начале ряда
|находящаяся в конце ряда
94. ~Варианта с наибольшей частотой:
|мода
|медиана
|дисперсия
|среднее квадратическое отклонение
|среднее арифметическое значение
95. ~Отдельные равные части, на которые разбивается вариационный ряд:
|квартили
|квинтили
|квантили
|децили
|процентили
96. ~Величины, делящие вариационный ряд на четыре равные части:
|квантили
|децили
|процентили
|квартили
|квинтили
97. ~Величины, делящие вариационный ряд на пять равных частей:
|квартили
|квантили
|квинтили
|децили
|процентили
98. ~Величины, делящие вариационный ряд на десять равных частей:
|квинтили
|квартили
|децили
|квантили
|процентили
99. ~Величины, делящие вариационный ряд на сто равных частей:
|децили
|квинтили
|процентили
|квартили
|квантили
100.~Процентили - это величины, делящие вариационный ряд на:
|пять равных частей
|четыре равные части
|сто равных частей
|десять равных частей
|равные части
101.~Квартили - это величины, делящие вариационный ряд на:
|сто равных частей
|пять равных частей
|четыре равные части
|десять равных частей
|равные части
102.~Децили – это величины, делящие вариационный ряд на:
|четыре равные части
|сто равных частей
|десять равных частей
|пять равных частей
|равные части
103.~Квинтили – это величины, делящие вариационный ряд на:
|десять равных частей
|пять равных частей
|четыре равные части
|сто равных частей
|равные части
104.~Квантили – это величины, делящие вариационный ряд на:
|пять равных частей
|равные части
|десять равных частей
|четыре равные части
|сто равных частей
105.~Нижний квартиль - это … процентиль.
|10-ый
|25-ый
|50-ый
|75-ый
|99-ый
106.~Верхний квартиль - это … процентиль.
|10-ый
|25-ый
|50-ый
|75-ый
|99-ый
107.~Номер нижнего квартиля:
| 
| 
| 
| 
| 
108.~ Номер верхнего квартиля:
| 
| 
| 
| 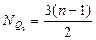
| 
109.~Мера разброса случайной величины от ее среднего значения:
|мода
|медиана
|дисперсия
|среднее квадратическое отклонение
|выборочное среднее значение
110.~Дисперсия - это:
|мера разброса случайной величины от ее среднего значения выраженная в процентах
|мера разброса случайной величины от ее среднего значения
|квадратный корень из среднего
|показатель центральной тенденции
|мера тесноты связи между признаками
111.~Среднее квадратическое отклонение - это:
|квадратный корень из дисперсии
|мера разброса случайной величины от ее среднего значения
|мера разброса случайной величины от ее среднего значения выраженная в процентах
|показатель центральной тенденции
|мера тесноты связи между признаками
112.~Квадратный корень из дисперсии - это:
|среднее квадратическое отклонение
|выборочное среднее значение
|мода
|медиана
|размах
113.~Разность между максимальным и минимальным значениями признака - это:
|размах
|среднее квадратическое отклонение
|дисперсия
|выборочное среднее значение
|медиана
114.~Если выборка задана вариационным рядом, то выборочная дисперсия определяется по формуле:
| 
| 
| 
| 
| 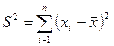
115.~Если выборка задана таблицей, то выборочная дисперсия определяется по формуле:
| 
| 
| 
| 
| 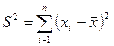
116.~  :
:
|выборочное среднее
|медиана
|выборочная дисперсия
|среднее квадратическое отклонение
|размах
117.~  :
:
|выборочное среднее значение
|медиана
|выборочная дисперсия
|среднее квадратическое отклонение
|размах
118.~ 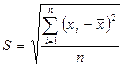 :
:
|выборочное среднее значение
|среднее квадратическое отклонение
|выборочная дисперсия
|медиана
|размах
119.~  :
:
|выборочное среднее значение
|выборочная дисперсия
|медиана
|среднее квадратическое отклонение
|размах
120.~  :
:
|среднее квадратическое отклонение
|размах
|выборочное среднее значение
|мода
|выборочная дисперсия
121.~Мера разброса случайной величины от ее среднего значения, выраженная в процентах:
|дисперсия
|коэффициент вариации
|мода
|выборочное среднее значение
|среднее квадратическое отклонение
122.~  :
:
|дисперсия
|мода
|выборочное среднее значение
|коэффициент вариации
|среднее квадратическое отклонение
123.~Если коэффициент вариации меньше 33%, то выборка:
|состоятельная
|смещенная
|однородная
|адекватная
|определенная
124.~Если коэффициент вариации больше 33%, то выборка:
|несостоятельная
|несмещенная
|неоднородная
|неадекватная
|неопределенная
125.~Характеристики генеральной совокупности:
|признаки
|параметры
|свойства
|значения
|частоты
126.~Средний вес юношей в возрасте 18 лет:
| Вес хi, (кг) | ||||||

|
|60
|63,9
|61,5
|62
|59,3
127.~Средний вес юношей в возрасте 18 лет:
| Вес хi, (кг) | ||||||
| Число обследованных νi | ||||||

| ||||||

|
|50,1
|69,8
|61,6
|46,2
|55,6
128.~Мода вариационного ряда:
| Масса хi, (кг) | ||||||
| Число обследованных νi |
|63
|61
|60
|62
|64
129.~Медиана вариационного ряда:
| Масса хi, (кг) | ||||||
| Число обследованных νi |
|63,5
|62,5
|61,5
|60,5
|64,5
130.~Средняя окружность головы у детей в возрасте от 1 до 2-х лет:
| Окружность головы хi, (см) | |||||

|
|40,2
|45,4
|50
|42,7
|47,3
131.~Средняя окружность головы у детей в возрасте от 1 до 2-х лет:
| Окружность головы хi, (см) | |||||
| Число обследованных νi | |||||

| |||||

|
|48
|45,5
|60,3
|40,9
|47,2
132.~Мода вариационного ряда:
| Окружность головы хi, (см) | |||||
| Число обследованных νi |
|46
|41
|45
|47
|48
133.~Медиана вариационного ряда:
| Окружность головы хi, (см) | |||||
| Число обследованных νi |
|41
|46
|45
|47
|48
134.~Средняя частота пульса:
| Частота пульса в 1 мин. хi | |||||||

|
|68
|72,1
|76
|70
|70,6
135.~Средняя частота пульса:
| Частота пульса в 1 мин. хi | |||||||
| Число обследованных νi | |||||||

| |||||||

|
|70,25
|68,33
|70,2
|70
|75
136.~Мода вариационного ряда:
| Частота пульса в 1 мин. хi | |||||||
| Число обследованных νi |
|70
|66
|68
|69
|72
137.~Медиана вариационного ряда:
| Частота пульса в 1 мин. хi | |||||||
| Число обследованных νi |
|66
|68
|69
|70
|72
138.~Среднее содержание сахара в крови:
| Уровень сахара в крови хi, (мг %) | ||||||||||

|
|101
|102
|100
|99
|98
139.~Среднее содержание сахара в крови:
| Уровень сахара в крови хi, (мг %) | |||||||||
| Число обследованных νi | |||||||||

| |||||||||

|
|100,1
|102,3
|105,1
|99,8
|95,2
140.~Медиана вариационного ряда:
| Уровень сахара в крови хi, (мг %) | |||||||||
| Число обследованных νi |
|100
|102
|105
|99
|95
141.~Мода вариационного ряда:
| Уровень сахара в крови хi, (мг %) | |||||||||
| Число обследованных νi |
|102
|100
|105
|99
|95
142.~К показателям разнообразия вариационного ряда не относится:
|мода
|дисперсия
|среднее квадратическое отклонение
|размах
|коэффициент вариации
143.~Некоторое предположение о параметрах известных распределений или о виде неизвестного закона распределения, выдвигаемое в качестве предварительного, условного объяснения называется:
|постулатом
|теоремой
|гипотезой
|аксиомой
|леммой
144.~Гипотеза об отсутствии различий между группами, либо об определенных значениях параметров, либо о соответствии распределения нормальному закону называется:
|проверяемой
|альтернативной
|нулевой
|ложной
|истинной
145.~Гипотеза о существовании различий между группами, либо об отличающихся от заданных значениях параметров, либо о несоответствии распределения нормальному закону, называется:
|нулевой
|проверяемой
|альтернативной
|ложной
|истинной
146.~Гипотеза о виде неизвестного закона распределения случайной величины называется:
|альтернативной
|нулевой
|непараметрической
|истинной
|параметрической
147.~Правило, которое используется для проверки нулевой гипотезы, называется:
|мощностью критерия
|статистическим критерием
|доверительной вероятностью
|уровнем значимости
|законом распределения
148.~Значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения, называется:
|табличным
|наблюдаемым
|критическим
|определенным
|средним
149.~Вероятность отвергнуть правильную нулевую гипотезу называется:
|ошибкой второго рода
|стандартной ошибкой
|ошибкой первого рода
|средней ошибкой
|доверительная ошибка
150.~Вероятность принять неправильную нулевую гипотезу называется:
|ошибкой первого рода
|стандартной ошибкой
|ошибкой второго рода
|средней ошибкой
|доверительной ошибкой
151.~Вероятность совершения ошибки первого рода называется:
|доверительной вероятностью
|мощностью критерия
|стандартной ошибкой
|уровнем значимости
|средней ошибкой
152.~Вероятность не совершить ошибку первого рода называется:
|мощностью критерия
|стандартной ошибкой
|средней ошибкой
|доверительной вероятностью
|уровнем значимости
153.~Уровень значимости обозначается:
| γ
| р
| n
| μ
| σ
154.~Доверительная вероятность обозначается:
| γ
| n
| р
| μ
| σ
155.~Величина уровня значимости для иссследований в фармации, медицине и биологии:
|0,01
|0,001
|0,05
|0,005
|0,1
156.~Величина уровня значимости для разработки стандартов:
|0,01
|0,05
|0,001
|0,005
|0,1
157.~Основная и альтернативная гипотезы выдвигаются на... этапе.
|2
|3
|1
|4
|5
158.~Уровень значимости задается на... этапе.
|3
|2
|4
|5
|1
159.~Наблюдаемое значение статистики критерия вычисляется на... этапе.
|4
|5
|3
|1
|2
160.~Табличное значение статистики критерия вычисляется на... этапе.
|3
|4
|2
|5
|1
161.~Сравнение наблюдаемого и табличного значений статистик критерия проводится на... этапе.
|3
|5
|2
|4
|1
162.~Вывод о правильности гипотезы делается на... этапе.
|3
|2
|5
|4
|1
163.~На первом этапе проверки статистической гипотезы:
|задается уровень значимости
|вычисляется наблюдаемое значение статистического критерия
|определяется табличное значение статистического критерия
|выдвигаются основная и альтернативная гипотезы
|проводится сравнение наблюдаемого и табличного значений критерия
164.~На втором этапе проверки статистической гипотезы:
|выдвигаются основная и альтернативная гипотезы
|вычисляется наблюдаемое значение статистического критерия
|задается уровень значимости
|определяется табл
|
|
|


