 |
Построение овала по двум осям
|
|
|
|
Последовательность построений (рис.2.17)
1). Заданы большая АВ и малая СD оси овала (рис.2.17а);
2).Соединим точки А и С. На этой прямой откладываем точку М: СМ=АО-ОС= СК (рис.2.17б);
3).Отрезок АМ делим пополам, и из середины этого отрезка восстанавливаем перпендикуляр до пересечения с осями овала в точках О1 и О4 (рис.2.17в);
4).Строим точки, симметричные точкам О1 и О4, получаем О2 и О3 (рис.2.17г);
5).Проводим линии центров О1О3, О1О4, О2О3, О2О4 (рис.2.17д);
6).Из центра О4 проводим дугу радиусом R1=О4С до пересечения с линиями центров О4О1 и О4О2 в точках 1 и 2. Аналогично находим точки 3 и 4 (рис.2.17е);
7).Замыкающие дуги овала проводим из центров О1 и О2 радиусом R2=О1А (рис.2.17ж).
8) Результаты построения – рис. 2.17з.
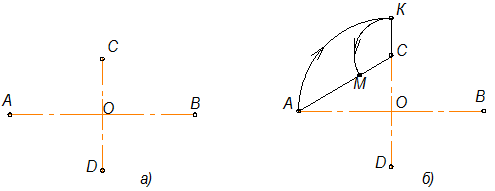
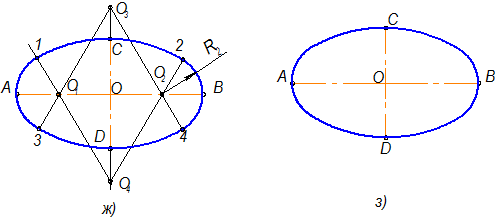
Рис.2.17
Выполнение чертежей деталей, имеющих сопряжения
Рис.2.18
Построение чертежа такой детали (рис.2.18) следует начинать с анализа геометрических элементов, составляющих изображение детали, и определения ее габаритных размеров. Затем следует продумать, какие геометрические построения нужно выполнить на чертеже. Соответственно габаритным размерам детали выбирают масштаб изображения. Построение рекомендуется выполнять в такой последовательности (рис.2.19):
1).Нанести осевые и центровые линии (рис.2.19а);
2).Провести окружности, центры которых расположены на пересечении центровых линий (рис.2.19б);
3).Выполнить сопряжения с указанием вспомогательных построений, необходимых для определения центров и точек сопряжения:
а) между окружностями Ø32 построить наружное сопряжение радиусом R24 аналогично построениям на рис.2.13;
б) между окружностями Ø32и Ø44 построить внутреннее сопряжение радиусом R76 аналогично построениям на рис.2.13;
|
|
|
в) выполнить построения для проведения касательной к окружностям Ø32 и Ø44, построить касательную аналогично построениям на рис.2.16. Построения показаны на рис. 2.19 в, г.
4).Нанести размерные линии и проставить размерные числа.
В Н И М А Н И Е!
Вспомогательные построения необходимо оставить на чертеже.
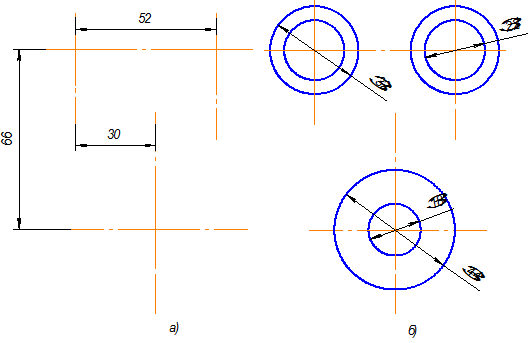
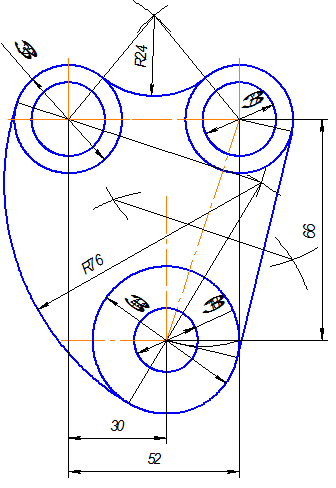
д)
Рис.2.19
Уклон
Уклон – это тангенс угла наклона одной прямой к другой (рис.2.20).
Возьмем произвольный масштабный отрезок (а). Построим прямоугольный треугольник
Рис.2.20
i = tg α =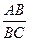 
=15:75=20%
На чертеже уклон задают или в процентах (рис.2.21) или отношением чисел (рис.2.22). Уклон 1:5 означает, что на пять единиц длины мы имеем одну единицу высоты. Т.е. прямая АС имеет уклон к ВС 20% или 1:5.
На чертежах уклоны обозначаются специальным знаком, см. ГОСТ 2.304-81. Острый угол знака уклона должен быть направлен в сторону снижения высоты, одна сторона угла параллельна полке линии-выноски.
Рис.2.21 Рис.2.22
Уклон используется, например, при изготовлении фасонного проката: швеллеров, двутавров, тавровых профилей и т.п.
Рассмотрим пример построения уклона внутренней грани нижней полки швеллера (рис.2.23).
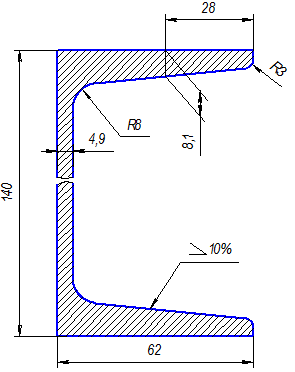
Рис.2.23
1. По данным размерам находим точку А, через которую пройдет заданный уклон (рис.2.24).
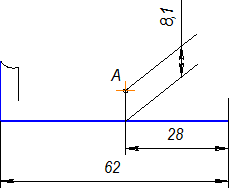
Рис.2.24
3. На свободном поле чертежа строим уклон 10% (1:10 = 10:100) и через точку А проводим прямую, параллельную линии уклона.
Выбираем масштабный отрезок любой величины.
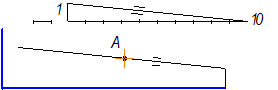
Рис.2.25
3. Дуга радиуса 3 – это сопряжение между линией уклона и вертикальной прямой. Строим по правилам построения сопряжения между прямыми (рис.2.26).
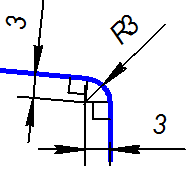
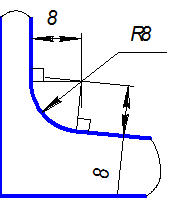
Рис.2.26 Рис.2.27
4. Дуга радиусом 8 – это сопряжение между линией уклона и вертикальной линией стойки (рис.2.27).
5. Аналогично строим верхнюю полку швеллера.
6. Так как высота стойки швеллера очень большая по сравнению с длиной полки, и стойка имеет постоянное сечение, то можно сделать разрыв, как показано на рисунке 2.28.
|
|
|
Рис.2.28
7. Проставляем размеры. Все построения на чертеже сохраняем.
2.9. Конусность 
Конусность – это отношение разности диаметров двух поперечных сечений усеченного конуса к длине между ними (рис.2.29).
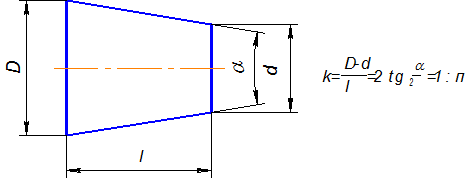
Рис.2.29
На чертеже конусность чаще всего выражается в процентах или соотношениях. Знак конусности острым углом направлен в сторону меньшего диаметра. Проставляют конусность или на полке линии-выноски (рис.2.30), или над осевой линией (рис.2.31).
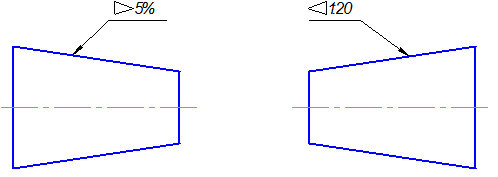
Рис.2.30
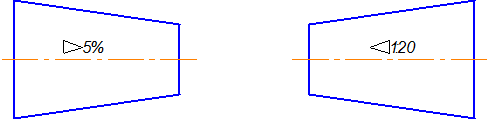
Рис.2.31
Если на чертеже указывают конусность, то на стержне и в отверстии размеры проставляют по разному, исходя из технологии изготовления конуса, так как нормальная конусность заложена на станках с программным управлением. Поэтому нормальную конусность необходимо указывать, а «лишний» размер убирать.
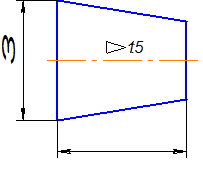
Рис.2.31
На коническом стержне из двух диаметров указывают больший, так как для изготовления детали нужно взять заготовку большего диаметра. Малый диаметр не указывают (рис.2.31).
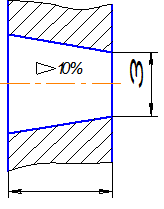
Рис.2.32
В отверстии из двух диаметров указывают меньший, так как для получения конусности нужно сначала просверлить отверстие диаметром, равным малому диаметру, а затем растачивать конусное отверстие (рис.2.32).
Конусности общего назначения стандартизованы. Их значение можно посмотреть в ГОСТ 8593-81.
В задании нужно построить конусность по размерам и вместо буквы n поставить числовое значение, полученноепри расчете по формуле на рис.2.29.Проставить размеры (рис.2.33)
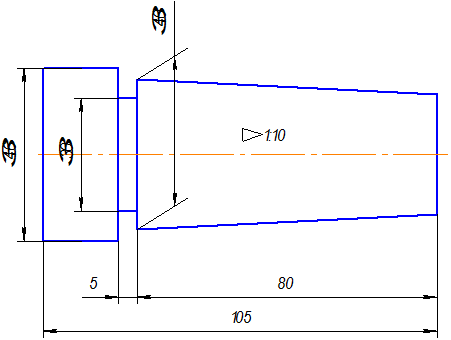
Рис.2.33
Контрольные вопросы
1. Сформулируйте понятие «сопряжение».
2. Какое сопряжение называется внешним, внутренним и смешанным?
3. Как определяются точки сопряжения?
4. Что называется уклоном и как определить величину уклона?
5. Что называется конусностью?
Нанесение размеров
(ГОСТ 2.307-68)
Основанием для определения величины изображенного изделия и его элементов служат размерные числа, нанесенные на чертеже.
Правила нанесения размеров на чертежах и других технических документах на изделия всех отраслей промышленности и строительства установлены ГОСТ 2.307 – 68. Размеры – это очень важная часть чертежа. Пропуск или ошибка хотя бы в одном из размеров делают чертеж непригодным к использованию.
|
|
|
Поэтому простановка размеров – одна из наиболее ответственных стадий при изготовлении чертежа.
При выполнении первых учебных чертежей студенту нужно знать основные правила нанесения размеров на чертежах.
|
|
|
