 |
Космические станции и космические исследования.
|
|
|
|
Цели запуска КА. Физика космического полета. Научные исследования и практическое использование КА. Космическая программа РК.
Задачи к ГЭ магистрантов
1. Получить формулу момента инерции тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня m, длина ℓ.
2. Получить формулу момента инерции тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей на расстоянии ¼ длины от одного из концов. Масса стержня m, длина ℓ.
3. Получить формулу момента инерции однородного диска относительно оси симметрии, перпендикулярной к плоскости диска. Заданы масса и радиус диска.
4. Получить формулу момента инерции тонкого проволочного кольца относительно оси, совпадающей с его диаметром. Радиус и масса кольца заданы.
5. И.1.266. Через неподвижный блок форме цилиндра массой m и радиуса R на нити перекинуты два груза массой  и
и  . Скольжения нити и трения в оси блока нет. Найти угловое ускорение цилиндра и отношение натяжения нитей
. Скольжения нити и трения в оси блока нет. Найти угловое ускорение цилиндра и отношение натяжения нитей  вертикальных участков нити в процессе движения. Показать, что при m
вертикальных участков нити в процессе движения. Показать, что при m  0
0  .+
.+
6. И.1.263. На однородный сплошной цилиндр (неподвижный блок) массы М и радиуса R плотно намотана нить, к концу которой прикреплен груз массы m. В момент t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени:
а) модуля угловой скорости цилиндра;
б) кинетической энергии всей системы.
7. И.1.288. Однородный цилиндр массы m и радиуса R в момент с намотанной нитью t = 0 отпускают, держа за конец нити. Цилиндр начинает опускаться под действием силы тяжести. Пренебрегая массой нити найти
|
|
|
а) угловое ускорение цилиндра
б) зависимость от времени мгновенной мощности, которую развивает сила тяжести.
8. И.1.81. На покоившуюся частицу массы m в момент t = 0 начала действовать сила, зависящая от времени по закону  , где
, где  – постоянный вектор,
– постоянный вектор,  - время, в течение которого действует сила. Найти
- время, в течение которого действует сила. Найти
а) импульс частицы после окончания действия силы
б) путь, пройденный частицей за время действия силы. +
9. И.1.82. Частица массы m в момент t = 0 начинает двигаться под действием силы  , где
, где  и
и  - постоянные. Найти путь, пройденный частицей, в зависимости от t.+
- постоянные. Найти путь, пройденный частицей, в зависимости от t.+
10. И.1.83. В момент t = 0 частица массой m начинает двигаться под действием силы  , где
, где  и
и  – постоянные. Сколько времени частица будет двигаться до первой остановки? Какой путь она пройдет за это время? Какова максимальная скорость частицы на этом пути?+
– постоянные. Сколько времени частица будет двигаться до первой остановки? Какой путь она пройдет за это время? Какова максимальная скорость частицы на этом пути?+
11. И.2.12. Найти максимальную температуру идеального газа в процессе
 , где
, где  и
и  - положительные постоянные, V – объем одного моля газа. +
- положительные постоянные, V – объем одного моля газа. +
12. Найти максимально возможную температуру идеального газа в процессе  =
=  , где
, где  и
и  - положительные постоянные, V – объем одного моля газа.+
- положительные постоянные, V – объем одного моля газа.+
13. И.2.13. Определить наименьшее возможное давление идеального газа в процессе, происходящем по закону  , где
, где 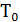 и
и  - положительные постоянные, V – объем одного моля газа.+
- положительные постоянные, V – объем одного моля газа.+
14. И.2.47. Идеальный газ с показателем адиабаты  расширяется по закону
расширяется по закону 
 , где
, где  . Первоначальный объем V0. В результате объем увеличился в
. Первоначальный объем V0. В результате объем увеличился в  раз. Найти молярную теплоемкость в этом процессе.+
раз. Найти молярную теплоемкость в этом процессе.+
15. И.2.48. Идеальный газ с показателем адиабаты  расширяют так, что сообщаемое газу тепло равно убыли его внутренней энергии. Найти молярную теплоемкость газа в этом процессе.+
расширяют так, что сообщаемое газу тепло равно убыли его внутренней энергии. Найти молярную теплоемкость газа в этом процессе.+
16. И.2.49. Один моль идеального газа с показателем адиабаты  совершает процесс, при котором давление
совершает процесс, при котором давление  , где
, где  . Найти молярную теплоемкость газа в этом процессе, При каком значении
. Найти молярную теплоемкость газа в этом процессе, При каком значении  теплоемкость становится отрицательной? Поссмотреть
теплоемкость становится отрицательной? Поссмотреть
|
|
|
17. И.2.50. Идеальный газ с показателем адиабаты  , при котором его внутренняя энергия
, при котором его внутренняя энергия  , где
, где  . Найти молярную теплоемкость в этом процессе.+ Поссмотреть
. Найти молярную теплоемкость в этом процессе.+ Поссмотреть
18. Используя теорему Остроградсского-Гаусса, определить напряженность электростатического поля равномерно по поверхности заряженной сферы. Радиус сферы R и поверхностная плотность заряда σ известны.+
19. Используя теорему Остроградсского-Гаусса, определить напряженность электростатического поля равномерно по объему заряженного шара радиуса R. Объемная плотность заряда ρ.=+
20. Используя теорему Остроградсского-Гаусса, определить напряженность электростатического поля равномерно по объему заряженного шара радиуса R. шара q.+
21. Используя теорему Остроградсского-Гаусса, определить напряженность электростатического поля равномерно по поверхности заряженной сферы радиуса R. Заряд сферы q.+
22. Получить формулу электроемкости однослойного плоского конденсатора. Параметры конденсатора заданы.
+
23. Получить формулу электроемкости однослойного сферического конденсатора. Параметры конденсатора заданы.+
24. Получить формулу электроемкости однослойного цилиндрического конденсатора. Параметры конденсатора заданы+
25. Получить формулу электроемкости двуслойного плоского конденсатора. Площадь обкладок S, расстояние между ними d. Толщина одного диэлектрика (ɛ1) равна d1. Диэлектрическая проницаемость второго диэлектирка равно ɛ 2 +
26. Получить формулу электроемкости двуслойного сферического конденсатора с диэлектирческами проницаемостями ɛ1 и ɛ 2.
Радиусы обкладок R1,R2, толщина первого диэлектрика а. +
27. Используя закон Кулона и принцип суперпозиции, определить напряженность электрического поля длинного, тонкого однорадного заряженного стержня длиной ℓ с зарядом q как функцию расстояния от одного из его концов в точках, расположенных на линии стержня. Рассмотреть условия, при котором длина стержня много меньше расстояния до точки в которой определяется поле.+
28. Используя закон Кулона и принцип суперпозиции, определить напряженность электрического поля тонкого кольца радиуса R с равномерно распределенним зарядом q в точках на оси кольца, перпендикулярной к плоскости и проходящей через его центр.
|
|
|
Рассмортреть условие удаления точки бесконечность.
29. Используя закон Кулона и принцип суперпозиции, определить напряженность электрического поля тонкого диска радиуса R, на котором равномерно распределен заряд q, в точках на оси перпендикулярной к плоскости диска и проходящей через его центр, как функцию расстояния от центра. Рассмотреть предельные случай.
30. Исследовать кинематические и энергетические характеристики электрического колебательного контура. Заряд на пластинах которого изменяется по закону q=10-6 cos 4πt. Определить момент равенства кинетической и потенциальной энергии.
31. К источнику переменного напряжения U = 300 sin 200 πt подключены последовательно катушка индуктивностью 0,5 Гн, конденсатор емкостью 10 мкФ и активное сопротивление 100 Ом. Определить амплитудное значение силы тока, сдвиг фаз между током и напряжением, коэффициент мощности и потребляемую мощность.
|
|
|


