 |
Допустимые кольца и решётки
|
|
|
|
Лукин Михаил Александрович
_____________________
Научный руководитель:
д. ф.-м. н., профессор, зав. кафедрой алгебры и геометрии
Вечтомов Евгений Михайлович
_____________________
Рецензент:
к. ф.-м. н., доцент, доцент кафедры алгебры и геометрии
Чермных Василий Владимирович
_____________________
Допущен к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой Е. М. Вечтомов
«___»___________2005 г. Декан факультета В. И. Варанкина
Киров – 2005
Содержание
Введение........................................................................................ 3
§1. Допустимые кольца и решетки.............................................. 6
§2. Допустимые полутела.......................................................... 10
§3. О единственности расширения............................................ 12
Заключение................................................................................. 14
Библиографический список........................................................ 15
Введение
Теория полуколец является активно развивающимся разделом современной алгебры, находящим применения в компьютерной алгебре, идемпотентном анализе, теории оптимального управления.
Для получения новых конструкций полуколец может оказаться полезным понятие двойного расширения полуколец (или 0-1 расширения).
В работе исследуется следующий вопрос.Для каких кольца R, полутела U и ограниченной дистрибутивной решетки L существует 0-1-расширение кольца R и полутела U с помощью решетки L?
Полукольцом называется такая алгебраическая структура á S; +, ×, 0ñ, что á S; +, 0ñ - коммутативный моноид с нулем 0, á S, ñ - полугруппа и в S выполняются тождества a (b + c)= ab + ac, (a + b) c = ac + bc и a 0=0 a =0. Неодноэлементное полукольцо с делением, не являющееся кольцом, называется полутелом (с нулем). Если из полутела S исключить 0, то получим структуру á S; +, ñ, которую будем называть полутелом без нуля, или просто полутелом. Полукольцо с квазитождеством a + b =0 Þ a =0 назовем антикольцом. Полукольцо с тождеством a + a = a называется идемпотентным. А полукольцо с квазитождеством a + b = a + c Þ b = c называется сократимым.
|
|
|
Полукольцо S назовем 0-расширением полукольца K с помощью полукольца T, если на S существует такая конгруэнция s, что K @[0]s - изоморфно нулевому ядру - и S / s @ T. Аналогично, полукольцо S с единицей 1 называется 1-расширением полукольца K, возможно без нуля, с помощью полукольца T, если на S существует конгруэнция r, для которой K @[1]r - изоморфно единичному ядру - и S / r @ T. В отличие от колец данные расширения позволяют шире представлять сами полукольца, скажем, изучить симбиоз колец и полутел, или колец и антиколец (см. [1]).
Для произвольного полукольца S обозначим через R (S)множество всех аддитивно обратимых элементов в S, а через U (S) – множество всех обратимых элементов в S в случае, когда S обладает 1. Очевидно, что R (S) является кольцом и строгим идеалом полукольца S (т.е. a + b Î R (S) Þ a, b Î R (S)).
Пусть S / R (S)– фактор-полукольцо полукольца S по конгруэнции Берна, соответствующей идеалу R (S): s конгруэнтно t Û s + a = t + b для некоторых a, b Î R (S). Положительное регулярное полукольцо, все идемпотенты которого центральны, называются arp -полукольцом [2]. При этом положительность полукольца S с 1 означает, что все элементы вида a +1, a Î S, обратимы, а его регулярность означает разрешимость в S каждого уравнения axa = a.
Справедливы следующие утверждения.
1. Любое полукольцо S является 0-расширением кольца, изоморфного R (S), с помощью положительно упорядоченного полукольца [1]
2. Полукольцо S с 1 изоморфно прямому произведению кольца и антикольца тогда и только тогда, когда его идеал R (S) имеет единичный элемент, коммутирующий с каждым элементом из S [1].
|
|
|
3. Полукольцо S служит 0-расширением кольца с помощью полутела тогда и только тогда, когда идеал R (S) полульца S простой (т.е. ab Î R (S) влечет a Î R (S) или b Î R (S)).
4. Для полукольца S с 1 фактор-полукольцо S / R (S) является полутелом с нулем тогда и только, когда R (S) есть максимальный односторонний идеал в S.
В качестве следствия утверждений 2 и 4 очевидным образом формулируется критерий разложимости полукольца с 1 в прямое произведение кольца и полутела с нулем. Отметим также, что подпрямые произведения кольца и ограниченной дистрибутивной решетки абстрактно охарактеризованы в [3].
5. Для существования 1-расширения полукольца K, возможно не имеющего нуля, с помощью полукольца T необходимо и достаточно, чтобы K имело 1, а T было идемпотентным полукольцом с 1.
6. Любое arp - полукольцо S является 1-расширением полутела U (S) с помощью ограниченной дистрибутивной решетки S / r, где r - конгруэнция на S, такая, что a r b означает aU (S)= bU (S). Для коммутативных полуколец верно и обратное утверждение. См. [2].
7. Всякое полутело является 1-расширением сократимого полутела с помощью идемпотентного полутела [4].
Полукольцо S с 1 назовем 0-1-расширением полукольца K и полукольца без нуля L с помощью полукольца T, если на S существует такая конгруэнция r, что [0]ρ@ K, [1]r@ L и S / r @ T.
Пусть для кольца R, полутела U и ограниченной дистрибутивной решетки L существует 0-1-расширение кольца R и полутела Uс помощью решетки L. Соответствующую тройку < R, P, L > будем называть допустимой.
Допустимые кольца и решётки
Речь в главе пойдёт о решётке и кольце, состоящих в допустимой тройке.
Обозначим через D двухэлементную цепь.
Пусть имеется полукольцо S с конгруэнцией r, для которой [0]r@ R, [1]r@ P, F / r @ D. Такое полукольцо S назовем дизъюнктным объединением кольца R и полутела P, и обозначим P 
R. Ясно, что " p Î P," r Î R, p × r Î R, p + r Î P.
С другой стороны, если любой элемент полукольца S с 1 либо обратим, либо имеет противоположный элемент, то S будет дизъюнктным объединением кольца R (S) и полутела U (S). При этом разбиение { R (S), U (S)} индуцирует искомую конгруэнцию r на S.
Предложение. В U 
R справедливы следующие утверждения а) аддитивная группа R делимая абелева группа. б) результат умножения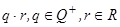 
определён единственным образом.
|
|
|
Доказательство. а) Пусть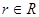 
, тогда 
, 
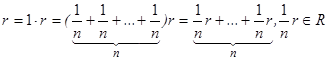ч.т.д.
б) Пусть мультипликативная операция задана. Если 
, то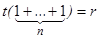 
. Умножив равенство на 
справа, получим 
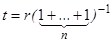, значит 
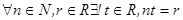. Рассмотрим результат умножения 
, пусть 
. Тогда 
, поэтому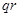 
есть элемент, складывая который 
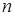раз получим 
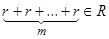. Из ранее доказанного следует, что такой элемент единственен, что завершает доказательство. 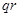есть решение уравнения 
в кольце 
.
Теорема 1. Для произвольного кольца R эквивалентны следующие условия:
1) существует допустимая тройка á R, U, L ñ, где L – любая дистрибутивная решетка с 1 ¹ 0;
2) существует полукольцо, являющееся дизъюнктным объединением кольца R и полутела U;
3) R – радикальное по Джекобсону кольцо, аддитивная группа которого есть делимая группа без кручения.
Доказательство.
1Þ2. Для данной тройки рассмотрим подходящие полукольцо S и конгруэнцию r. Поскольку D - подрешетка дистрибутивной решетки L с 0 и 1, в качестве дизъюнктного объединенияможно взять подполукольцо [1]rÈ[0]r в S.
2Þ1. Любая дистрибутивная решетка L обладает простым идеалом I, более того L \ I - дуальный идеал.
Поэтому в качестве полукольца S можно взять множество пар (i, r), i Î I, r Î R È(l, p), l Î L / I, p Î P с покоординатным сложением и умножением. Ввиду простоты I операции заданы корректно, аксиомы полукольца выполняются, поскольку они выполняются для левой координаты, как аксиомы решётки и для правой координаты, что следует из существования F, [0]r@ R, [1]r@ P, F / r @ L 2. Если в качестве конгруэнции g выбрать отношение равенства первых координат, то [0]g@ R, [1]g@ P, S / g @ L 2, что завершает доказательство.
Лемма. Пусть в кольце R " r $ r ¢ " t Î R, (r + r ¢ r + r ¢) t = 0Ù, (r + rr ¢ + r ¢) t = 0, тогда " r $ r ², r + r ² r + r ² = 0Ù r + r ² r + r ² = 0.
Доказательство. Пусть выполнено условие леммы, тогда, положим r ² =- r - r ¢ r. Имеем
r + r ² r + r ² = r +(- r - r ¢ r) r - r - r ¢ r = (r + r ¢ r + r ¢)(- r)=0
r + rr ² + r ² = r + r (- r - r ¢ r) - r - r ¢ r = (r + rr ¢ + r ¢)(- r)=0.
Кольцо R называется радикальным по Джекобсону, если оно совпадает со своим радикалом Джекобсона (см., например, [5]). Это означает, что операция «круговой композиции» r ° s = r + s + rs в R является групповой, с нейтральным элементом 0. Другими словами, в кольце R для любого элемента r существуетединственный элемент s, такой, что r + s + rs =0.
|
|
|
2)Þ3). P содержит Q +, иначе 1 + 1 = 1, умножив равенство на ненулевой элемент кольца r, имеем r + r = r Û r =0 – противоречие. Таким образом, R – полумодуль над Q + и, значит, модуль над Q. Поэтому < R,+ > - делимая абелева группа без кручения (подробно см. также предложение).
Множество T= Q + + R является подполутелом в U, поскольку
q 1 + r 1 + q 2 + r 2 = (q 1 + q 2) + (r 1 + r 2);
(q 1 + r 1)(q 2 + r 2) = (q 1 q 2 + q 1 r 2 + r 1 q 2 + r 1 r 2) = q 1 q 2 + (q 1 r 2 + r 1 q 2 + r 1 r 2);
t=q+r Þ 1=qt -1+rt -1 Þ t -1=q -1- q -1r t -1 Î Q+ + R.
Следовательно, для любого элемента 1+ r, r Î R найдётся, 1+ r ¢, r ¢ Î R что (1+ r)(1+ r ¢) = (1+ r ¢)(1+ r) = 1. Из дистрибутивности следует, что 1+ r + rr ¢ + r ¢ = 1+ r + r ¢ r + r ¢ = 1. Умножая последнее равенство на любое t Î R, имеем (r + r ¢ r + r ¢) t = 0Ù(r + rr ¢ + r ¢) t = 0, значит, в виду леммы, R радикально по Джекобсону.
3)Þ2). Поскольку R радикально по Джекобсону, алгебра Q + ´ R с операциями
(q 1, r 1) + (q 2, r 2) = (q 1 + q 2) + (r 1 + r 2), (q 1, r 1)×(q 2, r 2) = (q 1 q 2, q 1 r 2 + r 1 q 2 + r 1 r 2)
является полутелом с единичным элементом (1,0). А множество S @(Q + È{0})´ R с теми же операциями совпадает с (Q + ´ R) 
({0}´ R) = (Q + ´ R) R.
Примеры. 1. Любое ниль-кольцо радикально по Джекобсону. В частности таково кольцо с нулевым умножением.
Ещё одним частным случаем является нильпотентное кольцо R, порождённое одним элементом e.
Пусть e - образующий. Поскольку в качестве элементов R выступают p 1 e + p 2 e 2 + … + pn -1 e n -1, pi Î Q, n - наименьшая нулевая степень e, T 
R - в точности совпадает с одним из двух полуколец.
(q + q 1 e + q 2 e 2 + … + qn -1 e n -1, p 1 e + p 2 e 2 + … + pn -1 e n -1) q Î Q +, qi, pi Î Q или
(q + q 1 e + q 2 e 2 + … + qn -1 e n -2, p 1 e + p 2 e 2 + … + pn -1 e n -1) q Î Q +, qi, pi Î Q
c операциями
(q 1, r 1) + (q 2, r 2) = (q 1 + q 2) + (r 1 + r 2), (q 1, r 1)×(q 2, r 2) = (q 1 q 2, q 1 r 2 + r 1 q 2 + r 1 r 2).
2. Радикальным по Джекобсону будет кольцо, совпадающее с подмножеством гипердействительных чисел R @ m (0). Это коммутативное кольцо без делителей нуля. " a Î m (0), a + x + ax = 0Û x = (- a)/(1+ a) Î m (0)
Моделью представленного полукольца является прямое произведение двух подмножеств кольца Q [ x ]: многочленов с неотрицательным свободным членом и многочленов с положительным свободным членом. Множество пар, вида (q + q 1 e + q 2 e 2 + … + qn -1 e l, p 1 e + p 2 e 2 + … + pn -1 e m) q Î Q +, qi, pi Î
Соответственно частному функций задаются все операции в этом множестве (разумеется, берётся не всё множество пар, а множество классов факторполукольца, где две пары эквивалентны тогда и только тогда, когда равны произведения их противоположных координат).
|
|
|
Этот пример легко обобщается для многочленов от произвольного множества переменных.
Допустимые полутела
Дальнейший ряд предложений направлен на отыскание всевозможных полутел P, что P R.
Замечания. 1. Пусть дано допустимое кольцо R, тогда множество элементов M = { m Î R, " r Î R | r ∙ m = m ∙ r =0} образует в нём подкольцо.
2. Множество элементов E = { e Î R,1+ e =1 } образует в M и в R двусторонний идеал с делимой аддитивной группой.
3.Множество Q + ×(R / I) является полутелом с операциями (q 1, r 1) + (q 2, r 2) = (q 1 + q 2) + (r 1 + r 2), (q 1, r 1)×(q 2, r 2) = (q 1 q 2, q 1 r 2 + r 1 q 2 + r 1 r 2), где I - произвольный идеал с делимой аддитивной группой кольца R.
Теорема 2. Пусть á R, U, D ñ - допустимая тройка и R ненулевое. Тогда множество Q + + R есть подполутело U, изоморфное ((R / I) ´ Q +), где I некоторый идеал аннулятора с делимой аддитивной группой. И существует канонический гомоморфизм a полутела U в кольцо R -модульных эндоморфизмов End R R, образ которого содержит Q +. Если правый аннулятор кольца R нулевой, то полутело Im a содержит подполутело, изоморфное ((R / I) ´ Q +).
Доказательство. Пусть T, R - из допустимой тройки. Любой элемент T представим в виде q + r, q Î Q +, r Î R. Два элемента q + r 1 и q + r 2 равны тогда и только тогда, когда 1+ r 1 - r 2 =1. С другой стороны, если 1+ r = 1, то 1+ r 1 + r =1+ r 1. Поэтому все элементы вида q + r + e, 1+ e =1 " e сливаются в классы q ×(R / I), где I - множество всех e.
Отображение j u: R ® uR, u Î U ввиду дистрибутивности и ассоциативности в U R является R – модульнымэндоморфизмом. Пусть j u + j v: R ®(u + v) R и j u × j v: R ® uvR, тогда отображение a: U ® End R R, сопоставляющее каждому элементу u Î U эндоморфизм j u - канонический гомоморфизм.
Пусть правый аннулятор R нулевой, тогда для двух элементов q 1 + r 1, q 2 + r 2, считая без ограничения общности, q 1 = q 2 + q 3 (q 3 может равняться нулю), " r, (q 1 + r 1) r =(q 2 + r 2) r Û(q 3 + r 1 - r 2) r = 0Þ q 3 =0, r 1 = r 2. Элементы q 1 + r 1 и q 2 + r 2 одинаково действуют на R только в случае равенства. Поэтому a - мономорфизм и Im a содержит подполутело, изоморфное ((R / I) ´ Q +).
Замечание. Система (Q + ×(R / I))È({0}× R) с операциями (q 1, r 1) + (q 2, r 2) = (q 1 + q 2) + (r 1 + r 2), (q 1, r 1)×(q 2, r 2) = (q 1 q 2, q 1 r 2 + r 1 q 2 + r 1 r 2) и произвольным идеалом аннулятора с делимой аддитивной группой I является дизъюнктным объединением. Сложение класса (R / I) с элементом кольца определяется как сложение любого элемента этого класса с элементом кольца.
|
|
|
