Механизм возникновения и направление распространения излучения

Содержание

1. Эффект Вавилова - Черенкова

2. Механизм возникновения и направление распространения излучения

3. История открытия

4. Излучение Вавилова-Черенкова

5. Применение излучения Вавилова-Черенкова

Список использованной литературы

Эффект Вавилова – Черенкова

Эффе́кт  Вави́лова —  Черенко́ва, Эффект Черенкова, излуче́ние Вави́лова —  Черенко́ва, черенко́вское  излуче́ние — свечение,  вызываемое  в  прозрачной среде заряженной частицей,  движущейся  со  скоростью,  превышающей фазовую скорость распространения света в  этой  среде.

В 1958 году Павел Черенков, Игорь Тамм и Илья Франк были  удостоены Нобелевской премии по физике с  формулировкой:  «За  открытие  и  истолкование  эффекта  Черенкова».

Детекторы,  регистрирующие  черенковское  излучение,  массого  используются  в физике высоких энергий для  регистрации релятивистских частиц и  определения  их  скоростей  и направлений  движения.  Если  известна  масса  порождающих  черенковское  излучение частиц,  то  сразу  определяется  их  кинетическая  энергия. 

 

 

История открытия

В 1934 году Павел Черенков, выполнял в лаборатории С. И. Вавилова исследования люминесценции жидкостей под воздействием гамма-излучения, обнаружил слабое голубое излучение неизвестной природы. Позже было установлено, что это свечение вызывается электронами, движущимися со скоростями, превышающими фазовую скорость света в среде. Быстрые электроны выбиваются из электронных оболочек атомов среды гамма-излучением.

Уже первые эксперименты Черенкова, предпринятые по инициативе С. И. Вавилова, выявили ряд необъяснимых особенностей излучения: свечение наблюдается у всех прозрачных жидкостей, причём яркость мало зависит от их химического состава и химической природы, излучение поляризовано с преимущественным направлением электрического вектора вдоль направления распространения частиц, при этом в отличие от люминесценции не наблюдается ни температурного, ни примесного тушения. На основании этих данных Вавиловым было выдвинуто основополагающее утверждение, что обнаруженное явление — не является люминесценцией, а свет излучают движущиеся в жидкости быстрые электроны.

Теоретическое объяснение явления было дано И. Таммом и И. Франком в 1937 году.

В 1958 году Черенков, Тамм и Франк были награждены Нобелевской премией по физике «за открытие и истолкование эффекта Черенкова». Манне Сигбан из Шведской королевской академии наук в своей речи на церемонии вручения премии отметил, что «Открытие явления, ныне известного как эффект Черенкова, представляет собой интересный пример того, как относительно простое физическое наблюдение при правильном подходе может привести к важным открытиям и проложить новые пути для дальнейших исследований».

Механизм возникновения и направление распространения излучения

Теория относительности гласит: ни одно материальное тело, включая быстрые элементарные частицы с высокими энергиями, не может двигаться со скоростью, превышающей скорость света в вакууме.

Но в оптически прозрачных средах скорость быстрых заряженных частиц может быть больше фазовой скорости света в этой среде. Действительно, фазовая скорость света в среде равна скорости света в вакууме, делённой на показатель преломления среды: При этом вода, например, имеет показатель преломления 1,33, а показатели преломления различных марок оптических стёкол лежат в пределах от 1,43 до 2,1. Соответственно, фазовая скорость света в таких средах составляет 50—75 % от скорости света в вакууме. Поэтому оказывается, что релятивистские частицы, скорость которых близка к скорости света в вакууме, движутся в таких средах со скоростью, превосходящей фазовую скорость света.

Возникновение излучения Черенкова аналогично возникновению ударной волны в виде конуса Маха от тела, движущегося со сверхзвуковой скоростью в газе или жидкости, например, ударная конусообразная волна в воздухе от сверхзвукового самолёта или пули.

Пояснить это явление можно по аналогии с волнами Гюйгенса, из каждой точки вдоль траектории движения быстрой частицы исходит сферический фронт световой волны, распространяющийся по среде со скоростью света в этой среде, причём каждая следующая сферическая волна испускается из следующей точки на пути движения частицы. Если частица движется быстрее скорости распространения света в среде, то она обгоняет световые волны. Совокупность касательных прямых к сферическим волновым фронтам, проведённых из точки проходящей через частицу образуют круговой конус — волновой фронт излучения Черенкова. Механизм явления был выяснен в работе И. Е. Тамма и И. М. Франка (1937), содержавшей и количественную теорию, основанную на уравнениях классической электродинамики. К тем же результатам привело и квантовое рассмотрение (В. Л. Гинзбург, 1940).

Условие возникновения Ч.—В. и. и его направленность могут быть пояснены с помощью Гюйгенса - Френеля принципа. Для этого каждую точку траектории заряженной частицы (например, А, В, С, D, рис. 1 и 2) следует считать источником волны, возникающей в момент прохождения через неё заряда. В оптически изотропной среде такие парциальные волны будут сферическими, т.к. они распространяются во все стороны с одинаковой скоростью u = с/n (здесь с — скорость света в вакууме, а п — показатель преломления света данной среды). Допустим, что частица, двигаясь со скоростью υ, в момент наблюдения находилась в точке Е. За t секунд до этого она проходила через точку А (расстояние до неё от Е равно υt). Следовательно, волна, испущенная из А, к моменту наблюдения представится сферой радиуса R = ut (на рис. 1 и 2 ей соответствует окружность 1). Из точек В, С, D свет был испущен во всё более и более поздние моменты времени, и волны из них представляют окружности 2, 3, 4. По принципу Гюйгенса парциальные волны гасят друг друга в результате интерференции всюду, за исключением их общей огибающей, которой соответствует волновая поверхность света, распространяющегося в среде.

Пусть скорость частицы υ меньше скорости света u в среде (рис. 1). Тогда свет, распространяющийся вперёд, будет обгонять частицу на тем большее расстояние, чем раньше он испущен. Общей огибающей парциальные волны при этом не имеют — все окружности 1, 2, 3, 4 лежат одна внутри другой. Это соответствует тому очевидному факту, что электрический заряд при равномерном и прямолинейном движении со скоростью, меньшей скорости света в среде, не должен излучать свет. Однако положение иное, если

υ > u = c/n, или βn > 1 (1)

(где β = υ/c), т. е. если частица движется быстрее световых волн. Соответствующие им сферы пересекаются (рис. 2). Их общая огибающая (волновая поверхность) — конус с вершиной в точке E, совпадающей с мгновенным положением частицы, а нормали к образующим конуса определяют волновые векторы (т. е. направление распространения света). Угол, который составляет волновой вектор с направлением движения частицы (см. рис. 2), удовлетворяет соотношению:

cos θ = u/υ = c/nυ = 1/βn. (2)

Такой же метод рассмотрения можно провести и для оптически анизотропных сред. При этом нужно учитывать, что скорость света в этой среде зависит от направления его распространения, поэтому парциальные волны не являются сферами. В этом случае обыкновенному и необыкновенному лучам будут соответствовать разные конусы и излучение будет возникать под разными углами θ к направлению распространения частицы согласно соотношению (2). Условие (1) для оптически анизотропных сред формулируется несколько иначе. Во всех случаях основные формулы теории хорошо согласуются с опытом.

Теория показала, что в оптически изотропной среде частица с зарядом е, прошедшая расстояние в 1 см со скоростью υ > u, излучает энергию:

(3)

ω = 2 nc/λ — циклическая частота света, λ — длина волны излучаемого света в вакууме). Подынтегральное выражение определяет распределение энергии в спектре Ч. — В. и., а область интегрирования ограничена условием (1).

Ч. — В. и. возникает при движении не только электрона в среде, но и любой заряженной частицы, если для неё выполняется условие (1). Для электронов в жидкостях и твёрдых телах условие (1) начинает выполняться уже при энергиях Черенкова-Вавилова излучение 105 эв (такие энергии имеют многие электроны радиоактивных процессов). Более тяжёлые частицы должны обладать большей энергией, например протон, масса которого в Черенкова-Вавилова излучение2000 раз больше электронной, для достижения необходимой скорости должен обладать энергией Черенкова-Вавилова излучение 108 эв (такие протоны можно получить только в современных ускорителях).

На основе Ч. — В. и. разработаны экспериментальные методы, которые широко применяются в ядерной физике как для регистрации частиц, так и для изучения их природы (см. Черенковский счётчик). Измерение θ в среде (радиаторе) с известным п или определение порога излучения позволяют получать из уравнения (2) или условия (1) скорость частицы. Установив скорость частицы и определив её энергию по отклонению в магнитном поле, можно рассчитать массу частицы (это было, например, использовано при открытии антипротона). Для ультрарелятивистских частиц условие (1) начинает выполняться уже в сжатых газах (газовые черенковские счётчики). Ч. — В. и., возникающее в атмосфере Земли, служит для изучения космических лучей.

Ч. — В. и. может наблюдаться в чистом виде только в идеальных случаях, когда частица движется с постоянной скоростью в радиаторе неограниченной длины. При пересечении частицей поверхности радиатора возникает т. н. переходное излучение. Оно было теоретически предсказано Гинзбургом и Франком (1946) и впоследствии исследовано экспериментально. Сущность его состоит в том, что электромагнитное поле частицы в вакууме и в среде различны. Любое изменение поля частицы всегда приводит к излучению света. При тормозном излучении (См. Тормозное излучение), например, оно вызывается изменением скорости частицы, а в случае переходного излучения тем, что меняются электромагнитные свойства среды вдоль траектории частицы. В тонком радиаторе, удовлетворяющем условию (1), переходное излучение в известной мере неотделимо от Ч. —В. и. В непрозрачных для света веществах возникающее на их границе переходное излучение играет доминирующую роль, т.к. интенсивность Ч. — В. и. снижена его поглощением. Переходное излучение возникает и тогда, когда не выполнено условие (1) (например, при малых скоростях частицы или, напротив, при излучении ультрарелятивистской частицы в области частот рентгеновского спектра, где n < 1 и, следовательно, всегда βn < 1). Интенсивность переходного излучения мала и обычно недостаточна для регистрации отдельной частицы. Для эффективной его регистрации может быть использовано суммирование излучения частицы при последовательном пересечении ею нескольких границ раздела.

В 1940 Э. Ферми обобщил теорию Ч. — В. и., приняв во внимание, что реальная среда обладает способностью поглощать свет по крайней мере в некоторых областях спектра. Полученные им результаты внесли существенные уточнения в теорию т. н. ионизационных потерь заряженными частицами (эффект поляризации среды).

Ч. — В. и. является примером оптики «сверхсветовых» скоростей и имеет принципиальное значение. Ч. — В. и. экспериментально и теоретически изучено не только в оптически изотропных средах, но и в кристаллах (оптически анизотропные среды), теоретически рассмотрено излучение электрических и магнитных диполей и мультиполей. Ожидаемые свойства излучения движущегося магнитного заряда были использованы для поисков магнитного монополя. Рассмотрено излучение частицы в канале внутри среды (например, излучение пучка частиц внутри волновода). При Ч. — В. и. новые особенности приобретает Доплера эффект в среде: появляются т. н. аномальный и сложный эффекты Доплера. Можно полагать, что всякая система частиц, способная взаимодействовать с электромагнитным полем, будет излучать свет за счёт своей кинетической энергии, если ее скорость превышает фазовую скорость света.

Теоретические представления, лежащие в основе Ч. —В. и., тесно связаны с др. явлениями, имеющими значение в современной физике (волны Маха в акустике, вопросы устойчивости движения частиц в плазме (См. Плазма) и генерации в ней волн, некоторые проблемы теории ускорителей частиц, а также генерация и усиление электромагнитных волн).

Лит.: Черенков П. А., Видимое свечение чистых жидкостей под действием γ-радиации, «Докл. АН СССР», 1934, т. 2, № 8: Вавилов С. И., О возможных причинах синего λ-свечения жидкостей, там же; Тамм И. Е., Франк И. М., Когерентное излучение быстрого электрона в среде, там же, 1937, т. 14, № 3; Черенков П. А., Тамм И. Е., Франк И. М., Нобелевские лекции, М., 1960; Джелли Дж., Черенковское излучение и его применения, пер. с англ., М., 1960; Зрелов В. П., Излучение Вавилова — Черенкова и его применение в физике высоких энергий, ч. 1—2, М., 1968.

 

 

 

Излучение Вавилова-Черенкова²

Особенное значение имеет специальное свечения, наблюдаемое под действием радиоактивных излучения ( - и -лучи). Как показал Павел Алексеевич Черенков, работавший под руководством С.И.Вавилова, свечение такого рода возникает у весьма разнообразных веществ, в том числе у чистых жидкостей, причём яркость мало зависит от их химического состава. Данное излучение имеет поляризацию и направленность вдоль направления движения частицы. Обнаружив, что свечение не испытывает тушения Вавилов пришел к выводу, что оно не является люминесценцией, как считалось ранее, и связал его происхождение с движением электронов через вещество. Полное разъяснение явления было дано в теоретическом исследовании Игоря Евгеньевича Тамма¹ и Илья Михайлович² Франка, которые показали, что свечение должно иметь место, если скорость электрона превосходит фазовую скорость света в данном веществе.

Пусть электрон двигается равномерно со скоростью 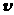вдоль линии ОL (рис. 1) сквозь некоторое вещество, к примеру воду.

При движении электрона через вещество имеется взаимодействие электрона с атомами этого вещества, в результате, которого часть энергии электрона может предаваться атомам, вызывая их ионизацию или возбуждение. Однако в данном вопросе нас не эти виды потерь энергии электроном. Как показывает детальное рассмотрение электрического поля, создаваемого движущимся электроном, могут иметь место и иные формы растраты энергии электроном. Рассмотрим случай. Пусть электрон со значительной скоростью движется по оси пустотелого канала, проделанного в веществе, так что он не испытывает непосредственных столкновений с атомами вещества. Оказывается, однако, что если диаметр канала значительно меньше длины волны света, то все же электрон теряет энергию в виде световой радиации сквозь поверхность, охватывающую ось цилиндрического канала. При этом мы можем для простоты считать среду вполне прозрачной, так что поток радиации беспрепятственно проходит через нее. Излучаемая энергия, конечно, заимствуется из энергии движущегося электрона, скорость которого должна уменьшиться вследствие торможения электрона в собственном поле. Именно это излучение представляет собой в чистом виде излучение Вавилова-Черенкова.

Расчет показывает, что рассматриваемое излучение и связанное с ним торможение возникают только в том случае, когда скорость электрона 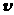больше фазовой скорости света в среде с, и прекращается когда скорость электрона уменьшается до этой скорости. Рассчитав электрическое и магнитное поля движущегося электрона со «сверхсветовой» скоростью электрона и образовав вектор Пойнтинга, можно вычислить поток радиации, излучаемой электроном.

При этом обнаруживается своеобразное распределениеизлучения в пространстве в идее узкого конического слоя, образующая которого составляет с осью движения угол , так что 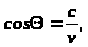где - фазовая скорость света; излучение оказывается поляризованным так, что его электрический вектор лежит в плоскости, проходящей через направление движения электрона. Все эти выводы теории оказалась в хорошем соответствии с результатами наблюдения свечения Вавилова-Черенкова.

Наиболее своеобразную особенность рассматриваемого излучения – его угловое распределение и необходимость соблюдения условия можно получить из довольно общих соображений. Представим себе электрон, движущийся со скоростью 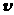вдоль линии ОL (рис.1), служащей осью узкого пустотного канала в однородном прозрачном веществе с показателем преломления n. Каждая точка линии OL, последовательно занимаемая электроном, является центром испускания света, но с запозданием, определенным величиной , где а – расстояние между 2 рассматриваемыми положениями электрона. Для того чтобы все волны, исходящие из этих последовательных положений, усиливались в результате взаимной интерференции, необходимо, чтобы разность фаз между ними была равно нулю при любом значении а. из рисунка 1 нетрудно увидеть, что это будет иметь место для направления, составляющего угол с направлением движения электрона, причем определяется из условия:

Откуда .

Действительно, фронт волны, исходящей из О, достигает положения АМ`, где А – новое положение электрона, через время ОМ`/ c = : электрон же достигнет точки А через промежуток времени . если указанные промежутки совпадают, , то волна из О и волна из А окажутся в одной фазе, какого бы ни было а.

Итак, мы видим, что направление максимальной интенсивности определиться углом образующей конуса с его осью ОL, удовлетворяющим условию . Если , т.е. скорость ниже фазовой скорости света, то соответствующие направление невозможно. Наоборот, при угол имеет вполне определенное значение, зависящие от скорости электрона и показателя преломления среды в согласии с полной теорией и опытными данными.

Легко видеть также, что если условие не соблюдается, то мы можем всегда разбить траекторию ОL на такие отрезки а, чтобы разность хода между волнами, исходящих из соответствующих двух соседних отрезков (т.е. из точек расположенных на расстоянии а) была равна 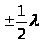. Иными словами, должно выполнятся условие

,

Откуда .

При соблюдении этого условия, свет, исходящий из соответствующих точек соседних участков, будет гаситься вследствие интерференции, и по данному направлению излучение распространяться не будет. Таким образом, единственное направление, по которому в силу взаимной интерференции волн может распространятся излучение, есть направление определяемое условием , имеющим смысл только в случае движения со сверхсветовой скоростью. Конечно, в реальном опыте световой конус не будет бесконечно тонким, ибо поток летящих электронов имеет конечную апертуру и известный разброс скоростей 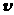, равно как и показатель преломления n имеет несколько различные значения для разных длин волн видимого интервала. Все это дает более или менее узкий конический слой около направления, определяемого условием .

Излучение Вавилова-Черенкова может вызываться не только движущимися частицами, но и каким-либо возбуждением, распространяющимся со скоростью, превышающей фазовую скорость света в среде. Допустим, например, что на границу сред падает волна с плоским фронтом АВ (рис 2). Вдоль границы раздела побежит возмущение со скоростью , где - фазовая скорость света в первой среде. Оно возбудит во второй среде излучение Вавилова-Черенова под углом к границе раздела. Угол определяется из соотношения , где - фазовая скорость света во второй среде. Замечая, что 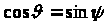, отсюда находим . Таким образом, преломление света можно трактовать, как эффект Вавилова-Черенкова, возбуждаемый во второй среде падающей волной. Также можно рассматривать и отражение света. В данном случае скорость волнового фронта V совпадает с фазовой скоростью 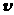. Отсюда получим, что , т.е. волновой фронт распространяется без изменения направления.

Эффекты, сходные с излучением Вавилова-Черенкова давно известны в гидро- и аэродинамике. Если, например, судно движется по поверхности спокойной воды со скоростью, превышающей, скорость распространения волн на поверхности воды, то возникающие под носом судна волны, отставая от него, образуют плоский конус волн, угол раскрытия которого зависит от соотношения скорости судна и скорости поверхностных волн. При движении снаряда или самолета со сверхзвуковой скоростью возникает звуковое излучение («вой»), законы распространения которого также связаны с образованием так называемого «конуса Маха». Явления эти осложняются сложностью уравнений аэродинамики.

Основные характеристики

Заряженная частица - электрон.

Порог

v > c/n, .

Вещество прозрачно для черенковского излучения, т.е.

|Im ε| ~<< Re .

Пороговая энергия (в МэВ)

,

n = n(ω). Так для воды при длине волны излучения ~0.4 мкм n ~1.3 и Ethr ~0.5 МэВ.

Спектр

Спектр непрерывный, практически нарастающий линейно до ωmaxпри n(ωmax) = c/v; ωmax ~< 10 - 30 эВ (ближний ультрафиолет; при больших частотах излучение происходит лишь в отдельных узких интервалах энергий). Спектральная интенсивность (на единицу пути)

.

Интегральная энергия излучения (в эВ/см)

.

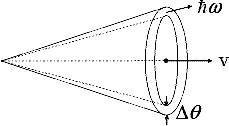Угловые характеристики

Конус с угловым раствором

.

Интервал углов

.

Поляризация излучения

Вектор электрического поля фотона лежит в плоскости скорости v и напавления излучения.

 

Поделиться:

Воспользуйтесь поиском по сайту: