 |
Порядок расчета разветвленной цепи постоянного тока
|
|
|
|
Пенза 2009
УДК 537.313(076.5)
ББК 22.33я73
И88
| Рецензент – | кандидат технических наук, старший научный сотрудник Н.Н. Григорьевский |
И88
Грейсух Г.И.
Исследование разветвленных электрических цепей. Правила Кирхгофа [Текст]: Методические указания к лабораторной работе / Г.И. Грейсух, С.А. Степанов. Пенза. 2009. – 10 с.
Дана методика и описан эксперимент по проверке первого и второго правил Кирхгофа. Эксперимент может быть проведен как на реальной лабораторной установке ЛКЭ-2П, так и на ее компьютерном имитаторе.
Предназначены для студентов всех специальностей, учебные планы которых предусматривают изучение курса физики.
Цель работы – экспериментальная проверка правил Кирхгофа по расчету разветвленных электрических цепей.
Приборы и принадлежности: лабораторный комплекс ЛКЭ-2П, включающий источник тока, мультиметр, магазин сопротивлений и комплект соединительных проводов, а также IBM-совместимый персональный компьютер и пакет компьютерных программ, имитирующих работу лабораторной установки.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Разветвленной электрической цепью называется цепь, содержащая узлы, т.е. места соединения не менее трех проводников с током. На рис. 1 дан пример разветвленной замкнутой цепи, включающей источники тока с ЭДС  ,
,  и суммарные сопротивления отдельных участков цепи
и суммарные сопротивления отдельных участков цепи  . Каждое из этих сопротивлений является суммой сопротивлений последовательно соединенных резисторов, соединительных проводов и внутренних сопротивлений источников тока.
. Каждое из этих сопротивлений является суммой сопротивлений последовательно соединенных резисторов, соединительных проводов и внутренних сопротивлений источников тока.
 |
Рис. 1. Разветвленная электрическая цепь
На рис. 2 показан выделенный из разветвленной цепи участок, содержащий сопротивление и источник тока. Такой участок называется неоднородным.
|
|
|
 |
Рис. 2. Неоднородный участок электрической цепи
В общем случае неоднородного участка цепи электрическое напряжение на концах участка вычисляется по формуле
 , (1)
, (1)
где  – разность потенциалов на концах участка;
– разность потенциалов на концах участка;
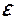 – ЭДС источника тока.
– ЭДС источника тока.
ЭДС в формуле (1) считается положительной в том случае, когда направление переноса положительных зарядов сторонними силами совпадает с направлением тока, т.е., когда ток внутри источника течет от отрицательного электрода к положительному. Этот случай представлен на рис. 2.
Зависимость между силой тока I, напряжением U на концах участка цепи и суммарным сопротивлением 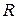 этого участка определяется законом Ома
этого участка определяется законом Ома
 . (2)
. (2)
С помощью этого закона в принципе можно выполнить расчет любой даже самой сложной разветвленной цепи. Однако задача существенно упрощается при использовании для расчета правил Кирхгофа. Они были установлены в 1847 г. применительно к электрическим цепям постоянного тока.
Чтобы сформулировать и уяснить смысл этих правил вновь обратимся к рис. 1. Представленная на нем цепь содержит два узла и три замкнутых контура. Причем под контуром понимается любая замкнутая цепь, которую можно выделить в разветвленной цепи. Если выполнять обход вдоль проводников замкнутого контура, начиная с выбранного узла, то обход завершится обязательно на том же самом узле. Токи в каждом участке цепи от узла до узла (ветви) обозначены соответственно  , а их направления выбраны произвольно. Ток, входящий в узел, принято считать положительным, а выходящий из узла – отрицательным.
, а их направления выбраны произвольно. Ток, входящий в узел, принято считать положительным, а выходящий из узла – отрицательным.
Первое правило Кирхгофа (правило узлов): алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.
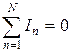 , (3)
, (3)
где  – число проводников, соединенных в узел;
– число проводников, соединенных в узел;
 – сила тока в
– сила тока в 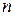 -ом проводнике, сходящемся в данном узле.
-ом проводнике, сходящемся в данном узле.
|
|
|
Это правило легко доказывается от противного. Если бы алгебраическая сумма токов была бы отлична от нуля, то в узле происходило бы накопление или уменьшение заряда, что, в свою очередь, приводило бы к изменению токов, т.е., чтобы токи во всех участках были постоянными по величине, условие (1) должно строго выполняться.
Второе правило Кирхгофа (правило контуров): в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма падений напряжений, на соответствующих участках этого контура, равна алгебраической сумме всех ЭДС в этом контуре:
 . (4)
. (4)
Данное правило является следствием закона Ома, и уравнение (4) можно получить, записав этот закон последовательно для всех участков замкнутого контура. Чтобы правильно записать суммы падений напряжения и ЭДС, необходимо выбрать направление обхода контура (произвольно, т.е. по ходу часовой стрелки или наоборот). Затем, двигаясь от какого-то узла, следует считать падения напряжения ( ), созданные токами, совпадающими по направлению с направлением обхода контура, положительными, а противоположные – отрицательными. ЭДС считаются положительными, если направление переноса положительных зарядов сторонними силами совпадает с направлением обхода контура. Данные правила знаков, конечно, условны, но безошибочный расчет возможен только при строгом применении одних и тех же правил для всех токов, напряжений и ЭДС.
), созданные токами, совпадающими по направлению с направлением обхода контура, положительными, а противоположные – отрицательными. ЭДС считаются положительными, если направление переноса положительных зарядов сторонними силами совпадает с направлением обхода контура. Данные правила знаков, конечно, условны, но безошибочный расчет возможен только при строгом применении одних и тех же правил для всех токов, напряжений и ЭДС.
Здесь отметим, что исторически сложившаяся терминология включает два эквивалентных термина – «напряжение» и «падение напряжения», которые в случае однородного участка цепи фактически характеризуют разность потенциалов, т.е. падение потенциала на данном участке.
Составляя уравнения вида (3) для узлов и вида (4) для контуров, получим систему линейных уравнений, включающую все токи, сопротивления, напряжения и ЭДС. При этом, как легко убедиться на примере любой разветвленной цепи, независимых уравнений по первому правилу можно составить только на одно меньше числа узлов, а по второму – на одно меньше числа контуров. Если число неизвестных величин, характеризующих разветвленную цепь, не превышает число независимых уравнений в системе, то все неизвестные могут быть найдены путем решения этой системы.
|
|
|
ПОРЯДОК РАСЧЕТА РАЗВЕТВЛЕННОЙ ЦЕПИ ПОСТОЯННОГО ТОКА
1. На электрической схеме обозначают токи во всех участках (ветвях) цепи, а их произвольно выбранные направления указывают стрелками.
2. Для  узлов цепи записывают (
узлов цепи записывают ( ) независимых уравнений по первому правилу Кирхгофа.
) независимых уравнений по первому правилу Кирхгофа.
3. Выделяют замкнутые контуры и после выбора направлений их обхода составляют уравнения по второму правилу Кирхгофа. Для разветвленной цепи, состоящей из  ветвей и
ветвей и  узлов, составляют (
узлов, составляют ( ) независимых уравнений по второму правилу Кирхгофа.
) независимых уравнений по второму правилу Кирхгофа.
4. Решают систему линейных уравнений относительно неизвестных параметров цепи.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
НА УСТАНОВКЕ ЛКЭ-2П
1. Включите мультиметр, установив режим измерения напряжения
20 В и, используя соединительные провода, измерьте ЭДС источника тока. Полученное значение внесите в табл. 1. При измерении отрицательная клемма источника должна соединяться с клеммой «com» мультиметра, а положительная клемма – с клеммой мультиметра « ».
».
2. Соберите электрическую цепь по схеме коммутаций (рис. 3). Отмаркированные на панели лабораторной установки, значения сопротивлений  схемы приведены в табл. 1. Более наглядная схема, эквивалентная собранной, представлена на рис. 4, где буквой
схемы приведены в табл. 1. Более наглядная схема, эквивалентная собранной, представлена на рис. 4, где буквой  обозначено внутреннее сопротивление источника тока, а стрелками показаны направления токов в каждой из ветвей цепи, соответствующие полярности источника тока и значениям сопротивлений
обозначено внутреннее сопротивление источника тока, а стрелками показаны направления токов в каждой из ветвей цепи, соответствующие полярности источника тока и значениям сопротивлений  .
.
3. Измерьте модуль падения напряжения на клеммах источника тока и на каждом из резисторов  . Результаты измерений внесите в табл. 1.
. Результаты измерений внесите в табл. 1.
Таблица 1
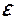 , В , В
|  , В , В
|  , В , В
| 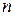
| 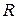 , Ом , Ом
|  , В , В
|  , А , А
|
 |
Рис. 3. Схема коммутации элементов
на панели экспериментальной установки
 |
Рис. 4. Эквивалентная схема исследуемой цепи
Внимание! Измеренное напряжение может быть как положительным, так и отрицательным. Поэтому, чтобы измеренные напряжения были положительными, необходимо обеспечить соответствие полярности при измерении напряжений на резисторах, направлениям токов через них, выбранным на рис. 4. Для этого при измерении напряжения щуп мультиметра, соединенный с клеммой «com», следует подключить к концу резистора, совпадающему с острием стрелки направления тока. Например, если на рис. 4 направление тока через резистор  выбрано от точки
выбрано от точки 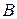 к точке
к точке  , то клемму «com» следует подключить к левой ножке резистора
, то клемму «com» следует подключить к левой ножке резистора  . Правую же его ножку следует соединить с клеммой мультиметра «
. Правую же его ножку следует соединить с клеммой мультиметра « ».
».
|
|
|
4. По формуле 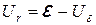 вычислите модуль падения напряжения на внутреннем сопротивлении источника тока и внесите полученный результат в табл. 1.
вычислите модуль падения напряжения на внутреннем сопротивлении источника тока и внесите полученный результат в табл. 1.
5. По закону Ома вычислите модули сил тока во всех ветвях (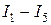 ) и внесите полученные результаты в табл. 1.
) и внесите полученные результаты в табл. 1.
6. Составьте для двух из трех узлов 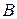 ,
,  , Е (см. рис.4) два уравнения по первому правилу Кирхгофа. При этом, как и принято, токи, входящие в узел, считайте положительными, а выходящие из узла – отрицательными. Значения алгебраических сумм для выбранных узлов внесите в соответствующую строку табл. 2.
, Е (см. рис.4) два уравнения по первому правилу Кирхгофа. При этом, как и принято, токи, входящие в узел, считайте положительными, а выходящие из узла – отрицательными. Значения алгебраических сумм для выбранных узлов внесите в соответствующую строку табл. 2.
Таблица 2
| Узел | 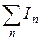 , А , А
| 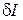 , % , %
|
7. Чтобы оценить, в какой степени экспериментально полученные результаты удовлетворяют первому правилу Кирхгофа, вычислите погрешность по формуле
 , (5)
, (5)
где  – –
| наименьший по модулю ток из набора токов  ; ;
|
 =2 – =2 –
| число уравнений, составленных по первому правилу Кирхгофа; |
 – –
| номер узла; |
 – –
| взятая по модулю левая часть уравнения, составленного по первому правилу Кирхгофа; определяющая значение абсолютной погрешности измерений, выполненных для  -го узла. -го узла.
|
8. Выберите в схеме, показанной на рис. 4, три контура, включающих ЭДС, и обозначьте стрелками направления обхода этих контуров.
9. Составьте для выбранных контуров уравнения по второму правилу Кирхгофа. При этом в уравнения, для контуров, включающих источник тока, не забудьте вместе с соответствующими напряжениями на резисторах включить и напряжение на внутреннем сопротивлении источника  . Напряжение на участке цепи, в котором направление тока совпадает с направлением обхода, считайте положительным, а в противном случае – отрицательным. Что же касается ЭДС, то ее следует взять со знаком «плюс», если при обходе контура движение осуществляется от отрицательной клеммы источника к положительной. В противном случае значение ЭДС берется со знаком «минус».
. Напряжение на участке цепи, в котором направление тока совпадает с направлением обхода, считайте положительным, а в противном случае – отрицательным. Что же касается ЭДС, то ее следует взять со знаком «плюс», если при обходе контура движение осуществляется от отрицательной клеммы источника к положительной. В противном случае значение ЭДС берется со знаком «минус».
10. Используя данные таб. 1, вычислите алгебраические суммы напряжений и ЭДС в каждом из контуров и внесите их в соответствующую строку табл. 3.
Таблица 3
| Контур |  , В , В
|  , В , В
|  , % , %
|
|
|
|
11. Чтобы оценить, в какой степени экспериментально полученные результаты удовлетворяют второму правилу Кирхгофа, вычислите погрешность по формуле
 , (6)
, (6)
где  – –
| число выбранных контуров; |
 – –
| значение абсолютной погрешности измерений, выполненных для  -го контура. -го контура.
|
|
|
|


