 |
Методика измерений и обработка результатов
|
|
|
|
Лабораторная работа № 3.06
Зависимость электропроводности полупроводников от температуры
Минск
2014
Лабораторная работа 3.06
Зависимость электропроводности полупроводников от температуры
1.Цель работы: изучение характера зависимости сопротивления полупроводников от температуры; определение энергии активации проводимости полупроводника.
2.Приборы и принадлежности: Сушильный шкаф, прибор для измерения сопротивления полупроводниковых образцов, мультиметр M890G с датчиком температуры (термопара), мультиметр M890Dдля измерения сопротивления образцов.
3.Вопросы для допуска к лабораторной работе:
1. Что представляет собой кристаллическое твердое тело?
2. Как изображаются на схемах значения энергии электронов в кристалле?
3. Выделите существенные признаки понятия «энергетическая зона».
4. Расскажите об основных идеях зонной модели твердого тела.
5. В чем различие между металлами, диэлектриками и полупроводниками с точки зрения зонной теории?
6. Что такое собственная проводимость полупроводников и как она зависит от температуры?
7. Что такое терморезистор?
8. Как получить примесные полупроводники p- и n-типа?
9. Объясните механизм образования примесной проводимости полупроводников с точки зрения зонной теории.
10. Что такое энергия активации? Как она определяется в данной работе?
11. Какова зависимость температурного коэффициента сопротивления α от температуры Т?
12. Существует ли четкая граница между полупроводниками и диэлектриками?
13. Возможна ли дырочная проводимость в металлах?
14. Может ли диэлектрик стать полупроводником? Проводником?
15. Как можно определить знак заряда основных носителей в полупроводниках?
|
|
|
16. Как можно определить знак заряда основных носителей в металлах?
17. Что называется валентной зоной, свободной зоной, запрещенной зоной.
18. При каком условии валентная зона и свободная зона являются зонами проводимости.
Теоретическое введение
В соответствии с основными положениями зонной теории электроны в атоме могут принимать только дискретные значения энергии, которые представляются в виде энергетических уровней. В одном изолированном атоме валентный электрон может иметь определенные дискретные значения энергии Е1, Е2 и т. д.
Предположим, что N одинаковых атомов, из которых состоит решетка твердого тела, удалены настолько далеко, что их взаимодействием можно пренебречь. Тогда энергетические уровни валентного электрона в каждом из N невзаимодействующих атомов одинаковы: каждый уровень в системе повторен N раз. При сближении атомов до расстояний, когда они образуют связанную систему, например кристалл, взаимодействие между атомами возрастает и приводит к «расщеплению» уровней, которые образуют энергетические зоны (на рис. 1 они заштрихованы). Вместо одного одинакового для всех атомов значения энергетического уровня возникает равная количеству атомов в кристалле совокупность очень близких, но не совпадающих между собой значений энергии. Величина расщепления уровней не одинакова. Сильнее расщепляются уровни, которые в атоме соответствуют внешним (валентным) электронам.
| Рис. 1 |
 На рис. 1 показано расщепление уровней в зависимости от расстояния между атомами. Верхние уровни начинают расщепляться при расстоянии
На рис. 1 показано расщепление уровней в зависимости от расстояния между атомами. Верхние уровни начинают расщепляться при расстоянии  , однако, образованные зоны еще не перекрываются.
, однако, образованные зоны еще не перекрываются.
| Рис. 2 |
 перекрываются. Перекрытие соседних зон происходит, начиная с расстояния
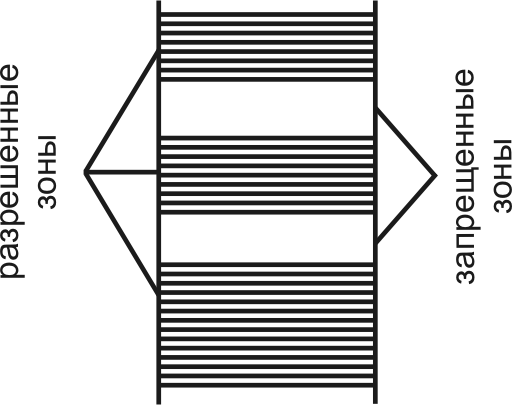
перекрываются. Перекрытие соседних зон происходит, начиная с расстояния  .Ширина зоны определяется величиной энергии связи между атомами и не зависит от числа атомов в кристалле. Так как N очень велико, то различия в энергиях между соседними уровнями в одной зоне крайне малы. Поэтому внутри зоны для перевода электрона с одного энергетического уровня на другой, соседний, требуется ничтожно малая энергия. Энергетическая область, в которой энергетические уровни отсутствуют, называется запрещенной. Электроны не могут иметь значения энергии, соответствующие запрещенной зоне (рис. 2).
.Ширина зоны определяется величиной энергии связи между атомами и не зависит от числа атомов в кристалле. Так как N очень велико, то различия в энергиях между соседними уровнями в одной зоне крайне малы. Поэтому внутри зоны для перевода электрона с одного энергетического уровня на другой, соседний, требуется ничтожно малая энергия. Энергетическая область, в которой энергетические уровни отсутствуют, называется запрещенной. Электроны не могут иметь значения энергии, соответствующие запрещенной зоне (рис. 2). |
|
|
Энергетические зоны не следует путать с пространственными зонами, т. е. областями пространства, где может находиться электрон.
Согласно принципу Паули на одном энергетическом уровне в любой разрешенной зоне не может находиться более двух электронов с противоположными значениями спина. Поэтому энергетические уровни заполняются парами электронов, начиная с «низких» уровней.
Самая верхняя разрешенная зона, полностью заполненная электронами, называется основной или валентной. Остальные, более высокие по значению энергии зоны, называются возбужденными. Первая возбужденная зона, которая примыкает к валентной, называется зоной проводимости.
В диэлектриках и полупроводниках валентные зоны целиком заполнены при температурах, близких к температуре абсолютного нуля, а зоны проводимости, отделенные от валентной запрещенной зоной, пусты (рис. 3, а, б).
У металлов либо нет запрещенной зоны, либо валентная зона не полностью заполнена даже при температуре абсолютного нуля (рис. 3, в). Поэтому даже при наличии слабого электрического поля металлические проводники начинают проводить электрический ток.
| Рис. 3 |
 Чтобы полупроводник начал проводить электрический ток, необходимо электронам из валентной зоны сообщить энергию достаточную для преодоления запрещенной зоны и попадания их в зону проводимости. Так, при нагревании электроны из валентной зоны переходят в зону проводимости, а в валентной зоне образуется свободное (вакантное) место, называемое дыркой. В это вакантное место могут переходить электроны с соседних уровней. В результате, при наложении электрического поля, и в валентной зоне, и в зоне проводимости создаются условия для возникновения тока. Наличие электронов в зоне проводимости обусловливает электронную проводимость, а наличие вакантных мест в валентной зоне – дырочную проводимость.
Чтобы полупроводник начал проводить электрический ток, необходимо электронам из валентной зоны сообщить энергию достаточную для преодоления запрещенной зоны и попадания их в зону проводимости. Так, при нагревании электроны из валентной зоны переходят в зону проводимости, а в валентной зоне образуется свободное (вакантное) место, называемое дыркой. В это вакантное место могут переходить электроны с соседних уровней. В результате, при наложении электрического поля, и в валентной зоне, и в зоне проводимости создаются условия для возникновения тока. Наличие электронов в зоне проводимости обусловливает электронную проводимость, а наличие вакантных мест в валентной зоне – дырочную проводимость.|
|
|
Чтобы оторвать электрон от атома и превратить его в электрон проводимости, атому необходимо сообщить некоторую энергию ∆Е, которую называют энергией ионизации. Тепловая ионизация происходит за счет энергии колебательного движения атомов. Возможна также ионизация путем бомбардировки потоком быстрых частиц, облучения электромагнитными волнами и т. д.
Принято считать, что если ширина запрещенной зоны при нормальной температуре больше ∆Е=2–3 эВ (1 эВ =1.6∙10-19 Дж), то кристалл является диэлектриком, а если меньше этого значения – полупроводником. Так, у алмаза, который является диэлектриком, ширина запрещенной зоны ∆Е= 5,2 эВ. К примеру, у наиболее распространенных полупроводников германия и кремния ширина запрещенной зоны составляет соответственно 0,72 эВ и 1,09 эВ.
Эта энергия, т.е. ширина запрещенной зоны ∆Е, заметно больше средней кинетической энергии теплового движения атома (кТ) при комнатной температуре. Например, при температуре Т=300К, kT =1,38∙10-23∙300 = 4,1∙10-21 Дж ≅0,025 эВ.
| Рис. 4 |
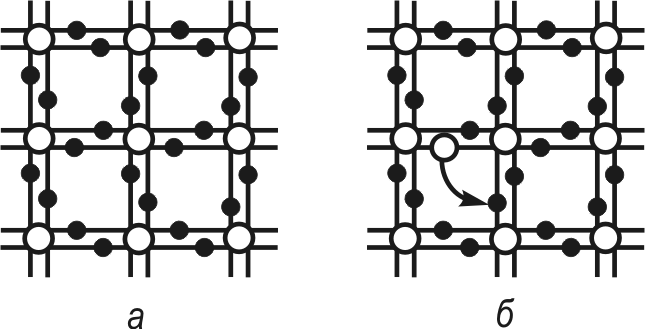 Рассмотрим схематично механизм проводимости чистого полупроводника на примере германия (рис. 4). На последней оболочке атома германия находятся четыре валентных электрона. Связь с соседними атомами создана путем обобщения одного электрона с соседним атомом. В результате такого обобщения последняя оболочка каждого атома заполняется до 8 электронов, что приводит к образованию ковалентной связи. Если при Т=0 К все электроны задействованы в связях между атомами (рис.6.4,а), то при
Рассмотрим схематично механизм проводимости чистого полупроводника на примере германия (рис. 4). На последней оболочке атома германия находятся четыре валентных электрона. Связь с соседними атомами создана путем обобщения одного электрона с соседним атомом. В результате такого обобщения последняя оболочка каждого атома заполняется до 8 электронов, что приводит к образованию ковалентной связи. Если при Т=0 К все электроны задействованы в связях между атомами (рис.6.4,а), то при  K часть электронов переходит в пространство между узлами кристаллической решетки, а на местах их пребывания образуются дырки (рис 4,б). Электроны могут рекомбинировать с ними, т. е. совершать переходы из каких-то квантовых состояний на незаполненные уровни (т. е. дырки).
K часть электронов переходит в пространство между узлами кристаллической решетки, а на местах их пребывания образуются дырки (рис 4,б). Электроны могут рекомбинировать с ними, т. е. совершать переходы из каких-то квантовых состояний на незаполненные уровни (т. е. дырки).
В отсутствие внешнего электрического поля по всему объему полупроводника установится равновесная концентрация дырок и свободных электронов. При наложении внешнего электрического поля на хаотичное движение электронов и дырок накладывается направленное движение, что приводит к упорядоченному движению носителей заряда. Электроны движутся в сторону, противоположную полю, а дырки – по его направлению. Согласно зонной теории, электроны из валентной зоны переходят в зону проводимости и полупроводник становиться электропроводящим. Рассмотренную электропроводность чистых полупроводников называют собственной.
|
|
|
При наличии в полупроводнике примесей картина электропроводности заметно меняется. Под примесями понимают атомы и ионы других элементов, различные дефекты и искажения в кристаллической решетке.

| Рис. 5 |
Один из его валентных электронов этого примесного атома является «лишним» и не может участвовать в связях с четырехвалентным и основными атомами (рис. 5,а). Небольшие изменения температуры способны оторвать этот электрон от «чужеродного» атома (рис. 5, б). В результате в полупроводнике возникает проводимость, которую называют электронной или проводимостью n-типа. Примесь, которая образует такую электропроводность, называют донорной.
В зонной теории возникновение проводимости n-типа выглядит следующим образом. Примесь с большей валентностью (в данном случае, мышьяк), чем у основного полупроводника, образует донорные примесные уровни, размещенные в запрещенной зоне и вблизи нижней границы зоны проводимости (рис. 5, в).
Энергия, отделяющая эти уровни от зоны проводимости, невелика, порядка 0,01 эВ (для германия с небольшой концентрацией примеси мышьяка  эВ). При температуре абсолютного нуля эти уровни так же, как и уровни валентной зоны, полностью заполнены. С повышением температуры с большей вероятностью происходит переход электронов с примесных уровней в зону проводимости, чем с уровней валентной зоны.
эВ). При температуре абсолютного нуля эти уровни так же, как и уровни валентной зоны, полностью заполнены. С повышением температуры с большей вероятностью происходит переход электронов с примесных уровней в зону проводимости, чем с уровней валентной зоны.
Если валентность примеси меньше валентности основного полупроводника, то создаваемая ими проводимость называется дырочной или проводимостью p-типа.
Механизм ее образования рассмотрим на примере все того же германия и трехвалентного индия (In). При замещении одного из основных атомов(Ge) примесным (In) с тремя валентными электронами одна из четырех связей является свободной, т.е. представляет собой место способное захватить электрон (рис. 6, а).
| Рис. 6 |
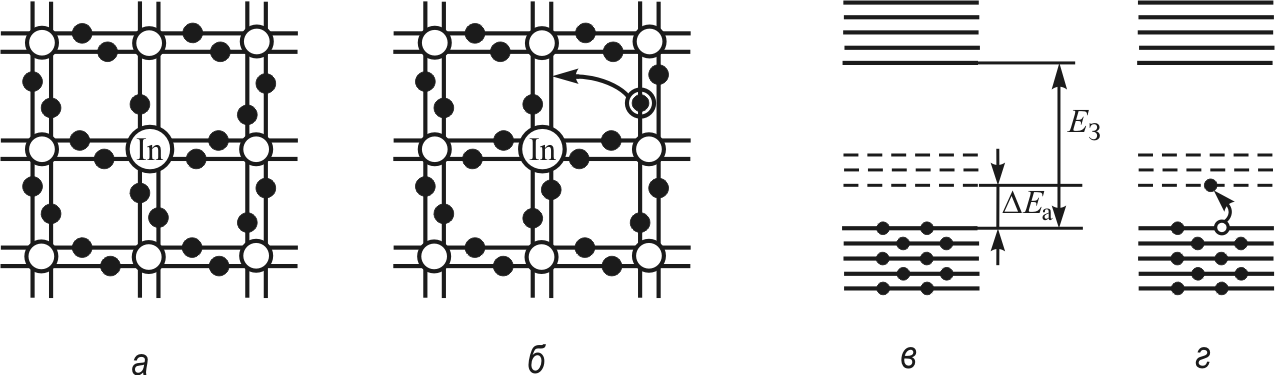 по всему кристаллу (рис. 6, б). Индий в германии обусловливает дырочную проводимость.
по всему кристаллу (рис. 6, б). Индий в германии обусловливает дырочную проводимость.|
|
|
Примеси, которые обеспечивают дырочную проводимость, называются акцепторными, а полупроводники с такой проводимостью – полупроводниками p-типа.
Согласно зонной теории трехвалентные примеси приводят к возникновению в нижней части запрещенной зоны дополнительных энергетических уровней, не занятых электронами при абсолютном нуле температуры.
При повышении температуры электроны с большей вероятностью будут переходить на них, чем на уровни зоны проводимости, так как ширина этих уровней намного меньше ширины запрещенной зоны и составляет сотые доли электронвольта (рис. 6, в, г).
Удельная электропроводность вещества зависит от концентрации носителей заряда и их подвижности. Под подвижностью носителей зарядов понимают отношение скорости их направленного движения, вызванного электрическим полем, к напряженности этого поля, т.е. скорость, которую получает электрон в электрическом поле, модуль напряженности которого  .
.
Для металлов удельная электропроводность  , где
, где  — заряд электрона;
— заряд электрона;  — концентрация электронов; µn — их подвижность.
— концентрация электронов; µn — их подвижность.
В полупроводниках с собственной проводимостью носителями заряда являются электроны и дырки, поэтому  , гдеµn и μp — подвижности электронов и дырок, соответственно.
, гдеµn и μp — подвижности электронов и дырок, соответственно.
Поэтому температурная зависимость удельной электропроводности  полупроводников обусловлена зависимостью от температуры концентрации свободных носителей заряда
полупроводников обусловлена зависимостью от температуры концентрации свободных носителей заряда  и их подвижностейµn(T) и µp(T).
и их подвижностейµn(T) и µp(T).
В металлах изменение температуры не влияет на концентрацию свободных электронов, поэтому зависимость  определяется только температурной зависимостью подвижности электронов µn(T).
определяется только температурной зависимостью подвижности электронов µn(T).
В полупроводниках же при изменении температуры изменяются и концентрация носителей заряда и их подвижности. Величина подвижности носителей заряда в кристаллических твердых телах определяется характером их рассеяния на дефектах кристаллической решетки. Дефекты кристаллической решетки могут быть вызваны разными причинами: наличием примесей, дислокациями, тепловыми колебаниями атомов относительно положения равновесия и др.
Температурная зависимость подвижности определяется тепловыми колебаниями атомов. При повышении температуры кристалла возрастает энергия тепловых колебаний, которая пропорциональна 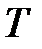 , а, следовательно, и амплитуда колебаний атомов в узлах кристаллической решетки. Чем больше амплитуда колебаний атомов, тем больше отклонение от идеальности кристаллической решетки и тем меньше подвижность носителей заряда.
, а, следовательно, и амплитуда колебаний атомов в узлах кристаллической решетки. Чем больше амплитуда колебаний атомов, тем больше отклонение от идеальности кристаллической решетки и тем меньше подвижность носителей заряда.
Зависимость подвижности от температуры µ (T)~ 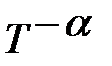 . Для полупроводников
. Для полупроводников  .
.
При изменении температуры полупроводника изменяется не только подвижность, но и концентрация электронов и дырок. Если повысить температуру бес примесного полупроводника, то часть атомов ионизируется, вследствие чего возникают свободные электроны и дырки в одинаковом количестве. Зависимость концентрации электронов и дырок от температуры имеет вид:  , где
, где 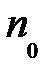 — наибольшая возможная концентрация электронов проводимости в данном полупроводнике (при
— наибольшая возможная концентрация электронов проводимости в данном полупроводнике (при  );
);  — энергия активации (ширина запрещенной зоны);
— энергия активации (ширина запрещенной зоны);  — постоянная Больцмана;
— постоянная Больцмана;  — абсолютная температура.
— абсолютная температура.
В примесном полупроводнике температурная зависимость концентрации носителей заряда, связанная с ионизацией примесей, также определяется формулой (3). Однако энергия ионизации примесей значительно меньше этой же энергии атомов основного вещества, и поэтому примесная проводимость наблюдается при значительно более низких температурах.
Общая удельная электропроводность примесного полупроводника  , где
, где  – концентрация электронов и дырок собственной проводимости,
– концентрация электронов и дырок собственной проводимости,  и
и  – их подвижности соответственно,
– их подвижности соответственно, 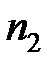 и
и  – концентрация и подвижность носителей заряда примесной проводимости. При смешанной проводимости носители зарядов, которые в большей степени влияют на проводимость, называются основными, а другие же – неосновными.
– концентрация и подвижность носителей заряда примесной проводимости. При смешанной проводимости носители зарядов, которые в большей степени влияют на проводимость, называются основными, а другие же – неосновными.
 Зависимость электропроводности полупроводника от температуры представлена в виде графика
Зависимость электропроводности полупроводника от температуры представлена в виде графика  на рис. 7.
на рис. 7.
Здесь  – удельная электропроводность полупроводника. Качественно эта зависимость разбивается на три участка. Участок ab соответствует примесной электропроводности при низких температурах.
– удельная электропроводность полупроводника. Качественно эта зависимость разбивается на три участка. Участок ab соответствует примесной электропроводности при низких температурах.
| Рис. 7 |
Таким образом, удельная электропроводность полупроводника
 , где σ0 – постоянная величина. Следовательно, удельное сопротивление полупроводника:
, где σ0 – постоянная величина. Следовательно, удельное сопротивление полупроводника:  , где
, где  — постоянная величина.
— постоянная величина.
Экспериментально обычно определяют не  , или
, или  , а сопротивление полупроводникового образца
, а сопротивление полупроводникового образца  .
.
Если учесть, что  , получим что сопротивление полупроводникового образца при температуре
, получим что сопротивление полупроводникового образца при температуре  :
:  , где
, где  постоянная величина. По этой формуле с достаточной степенью точности можно рассчитать сопротивление чистых полупроводников при
постоянная величина. По этой формуле с достаточной степенью точности можно рассчитать сопротивление чистых полупроводников при  500 К. Формула
500 К. Формула  может быть использована для определения энергии активации
может быть использована для определения энергии активации  . После ее логарифмирования, получим:
. После ее логарифмирования, получим:
 .
.
Следовательно, если экспериментально определить значения сопротивление полупроводника  при разных температурах и построить график
при разных температурах и построить график  , то по тангенсу угла наклона прямой
, то по тангенсу угла наклона прямой  можно определить энергию активации:
можно определить энергию активации: 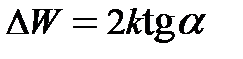 .
.
Отношение сопротивлений полупроводника  и
и  при двух значениях температуры
при двух значениях температуры  . Логарифмируя, получим
. Логарифмируя, получим  . Откуда
. Откуда 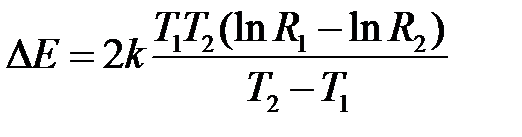 .
.
Методика измерений и обработка результатов
Лабораторная установка (рис. 8) состоит из сушильного шкафа СШУ 20, в который помещается зонд в виде пробирки с исследуемым образцом (терморезистором) и термопарой, приборов для измерения сопротивления (мультиметр M890D) и температуры (мультиметр M890G с термопарой).
| к образцу |
| к образцу |
| СШУ 20 с исследуемым образцом |
| M890G с термопарой |
| M890D для измерения R |
| Рис. 8 |

Сушильный шкаф (рис.6.9) представляет собой термокамеру объемом 10 л, с электронагревателем, мощность (рмах=150 Вт) которого можно регулировать реостатом расположенном на боковой стороне шкафа. Максимальная температура в термокамере не менее 150оС.
| Рис. 9 |

| Рис. 10 |
смеси порошкообразных оксидов металлов. Он имеет форму цилиндрического стержня 6 длиной 12 мм и диаметром 2 мм. На концы стержня надеты металлические колпачки с выводами, а боковая поверхность покрыта слоем эмалевой краски. Выводы терморезистора припаяны к двум медным проволокам 5; концы проволок подведены к двум винтовым зажимам 1, укрепленным на пластмассовой панели 2. В середине панели сделано отверстие, в которое вставлена картонная трубка 4, на верхний конец трубки надето резиновое кольцо 5, а на кольцо — стеклянная пробирка 7.
Пробирка с исследуемым об разцом помещается в изолированный сушильный шкаф типа СШ, в который вмонтирован реостат для регулировки тока нагрева. Температура измеряется термопарой подключенной к мультиметру M890G. Термопара вставляется в отверстие колодки, а к ее клеммам присоединяется прибор для измерения сопротивления.
Порядок выполнения работы
Задание 1
1. Подготовьте экспериментальную установку к работе. Включите мультиметр M890 D и установите переключатель рода работы в положение «измерение сопротивления 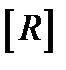 »; переключатель пределов измерения поставьте на значение 200 Ом при измерениях на медном образце или на значение 20 кОм при измерении сопротивления термистора.
»; переключатель пределов измерения поставьте на значение 200 Ом при измерениях на медном образце или на значение 20 кОм при измерении сопротивления термистора.
2. Соблюдая полярность, подключите термопару к гнездам на передней панели мультиметра M890G предназначенным для измерения температуры, установите переключатель рода работы в положение «измерение температуры  ».
».
3. Включите мультиметры, измерьте температуру и сопротивление образца при комнатной температуре.
4. Включите сушильный шкаф в сеть и, передвигая подвижный контакт реостата, отрегулируйте скорость его нагревания.
5. Нагревание исследуемого образца осуществляйте в интервале температур (20÷100) °С, измеряя его температуру и сопротивление с шагом ∆t= 10 °С.
Задание 2
1. Вычислите натуральный логарифм сопротивления  для каждого измерения и рассчитайте не менее пяти значений энергии активации (ширины запрещенной зоны)
для каждого измерения и рассчитайте не менее пяти значений энергии активации (ширины запрещенной зоны)  , полупроводниковоготермистора по формуле:
, полупроводниковоготермистора по формуле: 
2. Постройте в логарифмическом масштабе график зависимости  . Убедитесь, что зависимость близка к линейной и проведите аппроксимирующую прямую.
. Убедитесь, что зависимость близка к линейной и проведите аппроксимирующую прямую.
3. Вычислите угловой коэффициент наклона прямой к оси абсцисс и определите ширину запрещенной зоны 
4. Рассчитайте температурный коэффициент сопротивления термистора при нескольких значениях температуры и проверьте выполнимость теоретического соотношения 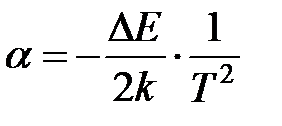 .
.
5. Результаты измерений и вычислений запишите в таблицу 1.
Таблица1
|
| ||||||
| № | Т, К | R, Ом | 
| 
| 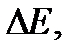 эВ эВ
|  , К-1 , К-1
|
| 1 | ||||||
|
|  эВ эВ
|  , К-1 , К-1
| ||||
По результатам выполнения каждого задания запишите ответы и сформулируйте выводы.
4. Выключите электрооборудование и приведите рабочее место в порядок
Вопросы для самоконтроля
1. Что представляют собой термометры сопротивления?
2. Почему и как изменяется сопротивление: а) металлов, б) полупроводников с ростом температуры?
3. Изобразите графически температурную зависимость удельного сопротивления а) чистого, б) примесного полупроводника.
4. Приведите схему энергетических уровней электронов в кристалле и укажите на ней соответствующие зоны.
5. Выделите существенные признаки понятий: «валентная зона», «зона проводимости».
6. Выведите выражение для расчета ширины запрещенной зоны ∆ Е.
7. Как создают донорные и акцепторные уровни в полупроводниках?
Литература
1. Физика. Учебник/И.Н. Наркевич, Э.И. Волмянский, С.И. Лобко.–Мн: Новое знание, 2004.
2. Физика. Учебное пособие/В.А. Бондарь, А.А. Луцевич, О.А. Новицкий и [др.]; Под общ. ред. В.А. Яковенко.–Мн: БелЭн, 2002.
3. Луцевич А.А. Физика: Весь школьный курс в таблицах/ А.А. Луцевич.– Мн: Юнипресс, 2010.
4. Общая физика. Практикум: Учеб. Пособие/ В.А. Бондарь и [др.]; под общ. ред. В.А. Яковенко.–Мн: Высшая школа, 2008.
5. Физический практикум/А.М. Саржевский, В.П. Бобрович, Г.Н. Борздов и [др.]; под ред. Г. С. Кембровского. Мн.; Университетское, 1986.
6. Савельев И.В. Курс физики: Учеб.: В 3-х т. Т. 2: Электричество. Колебания и волны. Волновая оптика. − М.: Наука. Гл. ред. физ.-мат. лит., 1989.
.
Пробирки с исследуемыми образцами помещаются в изолированный сушильный шкаф типа СШ, в который вмонтирован реостат для регулировки тока нагрева. Для измерения сопротивления образцов используется мультиметр типа мультиметр M890D, в режиме измерения сопротивления R. Температура измеряется термопарой подключенной к мультиметру M890G.Термопара вставляется в отверстие колодки, а к ее клеммам присоединяется прибор для измерения сопротивления.
Порядок выполнения работы
Задание 1
1. Подготовьте экспериментальную установку к работе. Включите мультиметр M890 D и установите переключатель рода работы в положение «измерение сопротивления 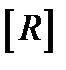 »; переключатель пределов измерения поставьте на значение 200 Ом при измерениях на медном образце или на значение 20 кОм при измерении сопротивления термистора.
»; переключатель пределов измерения поставьте на значение 200 Ом при измерениях на медном образце или на значение 20 кОм при измерении сопротивления термистора.
2. Соблюдая полярность, подключите термопару к гнездам на передней панели мультиметра M890G предназначенным для измерения температуры, установите переключатель рода работы в положение «измерение температуры  ».
».
3. Включите мультиметры, измерьте температуру и сопротивление образца при комнатной температуре.
4. Включите сушильный шкаф в сеть и, передвигая подвижный контакт реостата, отрегулируйте скорость его нагревания.
5. Нагревание исследуемого образца осуществляйте в интервале температур (20÷100) °С, измеряя его температуру и сопротивление с шагом ∆t= 10 °С.
6.Результаты измерений и вычислений запишите в таблицу 1.
Таблица 1
|
| ||||||
| № | Т, К | R, Ом | 
| 
| 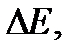 эВ эВ
|  , К-1 , К-1
|
| 1 | ||||||
|
|  эВ эВ
|  , К-1 , К-1
| ||||
Задание 2
5. Вычислите натуральный логарифм сопротивления  для каждого измерения и рассчитайте не менее пяти значений энергии активации (ширины запрещенной зоны)
для каждого измерения и рассчитайте не менее пяти значений энергии активации (ширины запрещенной зоны)  , полупроводниковоготермистора по формуле:
, полупроводниковоготермистора по формуле: 
6. Постройте в логарифмическом масштабе график зависимости  . Убедитесь, что зависимость близка к линейной и проведите аппроксимирующую прямую.
. Убедитесь, что зависимость близка к линейной и проведите аппроксимирующую прямую.
7. Вычислите угловой коэффициент наклона прямой к оси абсцисс и определите ширину запрещенной зоны 
4. Рассчитайте температурный коэффициент сопротивления термистора при нескольких значениях температуры и проверьте выполнимость теоретического соотношения 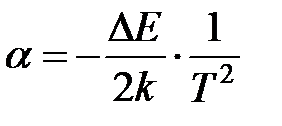 .
.
По результатам выполнения каждого задания запишите ответы и сформулируйте выводы.
|
|
|


