По результатам выполнения каждого задания сделайте соответствующие выводы.

Теоретическое введение

   Всякий реальный контур обладает активным сопротивлением. Энергия заряженного конденсатора при замыкании RLC-цепи постепенно расходуется на нагревание сопротивления. Поэтому свободные электромагнитные колебания (колебания заряда конденсатора, напряжения между обкладками конденсатора, силы тока в цепи) в RLC-контуре постепенно затухают. Для получения незатухающих колебаний в таком контуре необходимо подводить извне к нему энергию, компенсирующую тепловые потери. Для этого колебательный контур разрывают и подают на образовавшиеся контакты переменное напряжение от источника переменного тока (генератора):

                                                , где - амплитудное значение переменного напряжения; - циклическая частота.

Рис. 1

    Под действием приложенного напряжения в контуре устанавливаются электромагнитные колебания с частотой, равной частоте колебаний подведенного к контуру переменного напряжения , называемые вынужденными электромагнитными колебаниями. Такая схема подключения источника к контуру называется последовательным колебательным контуром (рис.1), так как все элементы RLC- контура и источник переменного напряжения соединены между собой последовательно.

По второму правилу Кирхгофа с учетом возникающей ЭДС самоиндукции  для этой цепи имеем:                                    .          С учетом того, что , а , получим

                                              .                            

                      

Разделив последнее выражение на L с учетом того, что - коэффициент затухания, а - циклическая частота собственных колебаний, получим дифференциальное уравнение второго порядка для вынужденных колебаний:

                         .                                       Полное решение неоднородного дифференциального уравнения, равно сумме решения соответствующего однородного линейного дифференциального уравнения и частного решения для. 

  Величина первого слагаемого этой суммы, т.е. общее решение однородного уравнения, имеет вид: ,                                      где q₀ – амплитуда заряда на конденсаторе;   - частота затухающих колебаний не равная циклической частоте источника (вынуждающей силы). Величина первого слагаемого этой суммы очень быстро убывает с течением временем, так как оно описывает свободные затухающие колебания в контуре.

Для того чтобы фаза тока равнялась , запишем частное решение уравнения в виде: , где 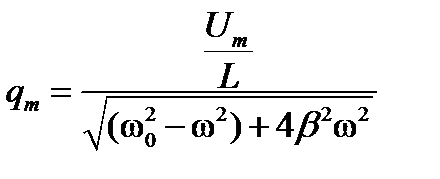                   , причем 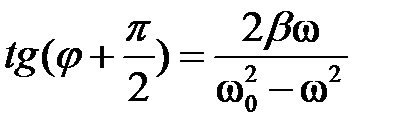. Подставив значения  и  в последнюю формулу получим   . 

Сила тока при установившихся вынужденных колебаниях:

, где     . Следовательно, , где                             

 

называется импедансом, т.е. полным сопротивлением электрической цепи, а

 и       называются и н д у к т и в н ы м и е м к о с т н ы м сопротивлениями (реактивными сопротивлениями).

                                     

 

Формула , соответствует закону Ома для амплитудных значений переменного тока. Амплитудное значение силы тока I_m зависит от ω, L, C и R. При ω→0, как и при ω→∞, I_m также стремится к нулю.

Резонансная частота не зависит от R, и равна:                                . При этой частоте максимальное значение амплитуды силы тока равно:                                          

                  

С ростом R, а следовательно, и коэффициента затухания , I_m уменьшается.

Зависимость амплитудных значений тока от частоты периодической вынуждающей разности потенциалов –    - для различных коэффициентов затухания  показана на рис. 2. Такие кривые называются резонансными амплитудно-частотными характеристиками.

 

Резонансные кривые амплитудных значений напряжения отличаются от резонансных кривых амплитуды тока. На рис. 3 приведены резонансные кривые изменения амплитудного значения напряжения на конденсаторе от частоты ω для разных значений коэффициента затухания , которые иллюстрируют увеличение остроты кривых с уменьшением , а также – уменьшение резонансной частоты с увеличением этого же коэффициента.

 

Из рис. 3 видно, что при ω→0 амплитудное значение напряжения U_mc стремится к U_m. Резонанс колебаний напряжения U_mc  наступает при частоте:

        

значение которой смещается в сторону меньших частот с ростом коэффициента затухания .

5. Методика измерений и обработка результатов

1.Соберите электрическую цепь по схеме, представленной на рис. 4.

 

Рисунок 4

2. Установите на звуковом генераторе начальное значение частоты

3. Регулятором напряжения установите на выходе звукового генератора напряжение, равное 30 мВ.

4. Включите в цепь последовательно с катушкой L и конденсатором C резистор R₁.

5. Измерьте значения силы тока I₁, I₂, I₃, изменяя частоту в интервале от 200 до 2,0 кГц через каждые 200 Гц, поддерживая напряжение в цепи неизменным с помощью регулятора напряжения для резистора R₁.

6. Замените резистор R₁ сначала резистором R₂, а затем резистором R₃ и повторите измерения при других значениях напряжения на выходе звукового генератора.

7. Результаты измерений занесите в таблицу.

                                                                                              Таблица

Частота , Гц			200	400	600	800	….	1600	1800	2000
1	R1=…... Ом	Сила тока I, мкА
	U1=……. В
2	R2=….. Ом
	U2=……. В
3	R3=….. Ом
	U3=……. В

 

8. По результатам измерений на миллиметровой бумаге постройте семейство амплитудно-частотных резонансных кривых.

9. По полученному графику зависимости I = I() и по максимальному значению силы тока I_m определите резонансную частоту .

10. По формуле     рассчитайте  значение резонансной частоты ν₀, подставляя значения L и C электрической цепи.

11. Сравните экспериментальное  и рассчитанное по формуле  значения резонансной частоты.

 

 

Частота , Гц			200	400	600	800	….	1600	1800	2000
1	R1=…... Ом	Сила тока I, мкА
	U1=……. В
2	R2=….. Ом
	U2=……. В
3	R3=….. Ом
	U3=……. В

 

  Вопросы для самоконтроля

1. Что называется колебательным контуром? Объясните возникновение вынужденных электрических колебаний в цепи переменного тока.

2. Выведите закон Ома для электрической цепи переменного тока, содержащей омическое сопротивление, емкость и индуктивность.

3. Получите дифференциальное уравнение вынужденных электрических колебаний.

4. Выведите формулу для резонансных частот колебаний силы тока и напряжения.

5. Изобразите и поясните ход резонансных кривых (амплитудных и фазовых).

6. Что такое полное сопротивление (импеданс) переменной электрической цепи?

7. Покажите, что при резонансе подводимая к контуру мощность равна мощности, рассеянной на омическом сопротивлении контура.

8. Чему равен сдвиг фаз между амплитудными значениями тока и напряжения на различных элементах RLC-цепи? Приведите векторные диаграммы.

9. Какова разность фаз между колебаниями напряжений на индуктивности и конденсаторе в последовательном контуре?

10. Выведите формулы для емкостного и индуктивного реактивных сопротивлений.

11. Чему равна амплитуда напряжений на индуктивности и конденсаторе при резонансе в последовательном контуре, если напряжение источника меняется по гармоническому закону?

12. Покажите, что при ω = ω₀ добротность колебательного контура равна коэффициенту усиления напряжения на конденсаторе, т.е. Q = Uс/E₀.

 

По результатам выполнения каждого задания сделайте соответствующие выводы.

Поделиться:

Воспользуйтесь поиском по сайту: