Равносильность предложений

Цель: сформировать понятие равносильности, научиться применять на практике полученные знания.

Эту тему дают обычно уже в конце 5 класса, когда ученики уже знакомы со знаком равносильности, который они использовали для краткой записи свойств делимости.

 Следует отметить, что понятие равносильности предложений относится не столько к математике, сколько к естественному языку. Как в обычном, так и в математическом языке одну и ту же мысль можно выразить несколькими разными способами. Например:

1) 32 < 64, 64 > 32.

2) Саша – брат Кати, Катя – сестра Саши. 

3) 5 x + 10 = 15,   x = 1.

 Обратите внимание на знак равносильности, который употребляется для краткой записи утверждения и обозначает, что два предложения означают одно и то же. Например:

3 < 5  5 > 3

 Обратите внимание на то, что если убрать из него стрелки слева и справа, то останется знак равенства. Знак равенства между двумя числовыми выражениями показывает, что эти выражения имеют одно и то же значение. Точно так же, как при преобразованиях числовых выражений мы пишем цепочку равенств:

Так же следует отметить, что равносильные высказывания одновременно истинны или ложны. Например, высказывания «Некоторые цветы бывают синими» и «Встречаются синие цветы» истинны. Но даже очень похожие по виду выказывания могут быть одно истинным, а другое ложным. Например, высказывания «Все кошки четвероногие» и «Все четвероногие - кошки», не являются эквивалентными, так как первое высказывание истинное, а второе ложное.

На этом этапе следует закрепить материал. Задания могут быть следующего содержания:

2) Выяснить, какие из приведенных пар высказываний являются эквивалентными:

а) Число x делится на 2.

Число x оканчивается на 2.

б) Хищники не едят траву.

Нет хищников, которые не едят траву.

в) Не все металлы тонут в воде.

Есть металлы, которые не тонут в воде.

 

3) Используя знак равносильности, записать решение уравнений:

а) 2 а – 3 = 25

б) 34 + 18 * в = 43

 

3) Записать в виде равенств утверждения, равносильные следующим:

а) Число m на 5 больше числа р.

б) При делении числа а на число b получается в частном с.

 

4) Какие из следующих утверждений верны:

а) Число x в 2 раза больше y x = y + 2

б) Число m составляет 30 % числа n m = n / 100 * 30

в) Углы А и В смежные Сумма углов А и В равна 180 градусов.

 

 

Отрицание высказываний

Эту тему можно ввести в начале 6 класса, т. к. здесь ученики начинают решать более сложные задачи, которые требуют правильности в рассуждениях.

Цель: сформировать понятие отрицания, научиться строить отрицание высказываний, изучить закон исключенного третьего, научиться применять на практике полученные знания.

Мотивация: нередко в жизни людям приходится спорить. Каждый в споре, доказывая свою правоту, убеждает собеседника, что тот не прав. Но всегда в споре кто-то прав, а кто-то ошибается. Тогда говорят, что их утверждения отрицают друг друга. Каждое из них называется отрицанием другого.

Приведем примеры предложений, в которых в каждой паре высказываний одно является отрицанием другого.

№	Высказывание	Отрицание
1.	У Маши есть котенок.	У Маши нет котенка.
2.	100 больше, чем 50.	100 не больше, чем 50.
3.	Верно, что все птицы летают.	Неверно, что все птицы летают.
4.	10 делится на 4.	10 не делится на четыре.
5.	Щенок Миши спит на кресле.	Щенок Миши не спит на кресле.

 

Вывод:  из таблицы ясно, что как высказывание, так и отрицание может быть ложным. Если высказывание – истина (ложь), то его отрицание - ложь (истина).

Далее необходимо переключить внимание учеников на математику, отметив, что в математике также нередко встречаются задачи, в которых приходится строить отрицания. Это необходимо для того, чтобы отбросить все лишние, «ненужные» случаи и получить единственно правильное решение.

Так как с отрицаниями нам приходится встречаться и в математике, и в жизни, очень важно научиться правильно формулировать отрицание любого заданного предложения. И на этом этапе необходимо дать определение отрицанию.

 Отрицание есть логическая операция, превращающая истинное высказывание в ложное, а ложное высказывание в истинное.

Символически отрицание записывается как 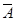 , где  – сложное или простое высказывание, а символы означают операцию отрицания. Читается: неверно, что А. Например:

В нашем доме живет белая кошка.

Его отрицание будет звучать следующим образом:

Неверно, что в нашем доме живет белая кошка.

Делаем вывод о том, что для формулировки отрицания сначала «мысленно» присоединяем к предложению слова «Неверно, что», а затем «обрабатываем» полученное отрицание так, чтобы оно звучало грамотно. Для этого рассмотрим таблицу:

№	Предложение	Первая формулировка отрицания	Вторая формулировка отрицания.
1.	Полуостров Таймыр – родина апельсинов.	Неверно, что полуостров Таймыр – родина апельсинов.	Полуостров Таймыр не является родиной апельсинов.
2.	У бабушки в деревне живут только куры.	Не верно, что у бабушки в деревне живут только куры.	У бабушки в деревне живут не только куры, но и гуси.
3.	Оля и Вася учатся в одной школе.	Не верно, Оля и Вася учатся в одной школе.	Оля и Вася учатся в разных школах.
4.	Все спотрсмены ловкие.	Не верно, что все спотрсмены ловкие.	Не все спотрсмены ловкие.
5.	Есть дома, которые имеют больше десяти этажей.	Не верно, что есть дома, которые имеют больше десяти этажей.	Нет домов, которые имеют больше десяти этажей.

 

Необходимо сформулировать закон исключенного третьего: если данное предложение истинно, то его отрицание ложно, и наоборот, если данное предложение ложно, то его отрицание истинно.

Примерные задания:

1. Скажите то же самое по-другому:

а) Неверно, что все млекопитающие живут на суше.

б) Неверно, что 5 делится на 2.

в) Неверно, что некоторые рыбы летают.

2. Построить отрицание предложений с помощью слова неверно и в более простой форме.

а) Сегодня будет солнечно.

б) Все собаки любят кошек.

в) Курица – домашняя птица.

г) Весной снег всегда тает.

д) 150 меньше 200.

е) Математика – точная наука.

3) Придумать свои предложения и построить их отрицание.

4) Доказать, что высказывание является ложным и построить его отрицание:

а) Число 0 является натуральным.

б) Между числами 4 и 5 нет натуральных чисел.

в) Неправильная дробь меньше единицы.

 

Логическое следование

Так как эта тема не входит в минимум содержания обучения, ее следует давать на кружках в 6 классе.

Цель: сформировать понятие логического следования, научиться применять на практике полученные знания.

Мотивация: Вспомните такие знаменитые высказывания:

Тише едешь – дальше будешь.

Подальше положишь – поближе возьмешь.

Или совсем простой пример из жизни:

Если вода нагревается, то она испаряется.

Что объединяет эти предложения?

Во всех трех предложениях мы из чего-то делаем вывод.

Рассмотрим следующее высказывание:

Если прошел дождь (А), то асфальт мокрый (В).

1) Если дождь на самом деле прошел, то асфальт действительно будет мокрым. В этом случае высказывание будет истинным.

2) Допустим, что А - ложное, т.е. дождя не было, но асфальт сырой. Сырым он мог оказаться после того как прошла поливочная машина. В этом случае высказывание А истинно.

3) Если дождя не было, то асфальт остался сухим. Высказывание истинно.

4) Представьте, что дождь прошел, а асфальт остается сухим. Это не возможно. Высказывание ложно.

Составим таблицу истинности:

№	А	В	А-В
1	и	и	и
2	и	л	л
3	л	и	и
4	л	л	и

 

Исходя из таблицы, можем дать определение логического следования.

Логическое следование – это логическая операция, которая объединяет два высказывания в такое новое высказывание, которое является ложным при истинности первого высказывания и ложности второго, во всех остальных случаях высказывание истинно.

В математике есть специальный знак следования , который соединяет два предложения с переменными и делает из них новое высказывание общего вида: из первого предложения следует второе. Первое предложение называют условием, а второе – заключением, или следствием первого.

«Если Р, то Q» или «Из Р следует Q».

Примерные задания:

1) Сформулировать предложения, используя глагол «следует»:

а) если животное млекопитающее, то оно кормит детей молоком;

б) если вода превратилась в лед, то ее температура отрицательная.

2) Назови условие и заключение:

а) Если число оканчивается на 0, то оно кратно 5.

б) Если сумма цифр числа делится на 3, то и само число делится на 3.

в) Если каждое слагаемое делится на некоторое число, то их сумма тоже делится на это число.

3) Прочитай высказывания и определи, истинны они или ложны. В каких высказываниях условие и заключение поменялись местами?

а) n кратно 8 n   кратно 4;

б) n кратно 4 n кратно 8;

 

Конъюнкция высказываний А В

Так как данная тема не входит в минимум содержания обучения, то ее можно дать ученикам на кружках в 6 классе.

Цель: сформировать понятие конъюнкции, отработать на практике полученные знания, научиться применять на практике.

Мотивация: Представьте себе такую ситуацию:

Ваша бабушка ходила в магазин и купила пряники и конфеты. На ваш вопрос, что она купила, она ответила: «Я купила пряники и конфеты.»

В этом случае бабушка сказала правду и ее высказывание – истина. Если бы бабушка солгала, она бы могла ответить следующим образом:

1) Я купила пряники, а конфет не было.

2) Я не купила пряники, но купила конфеты.

3) Я не купила ни конфет, ни пряников.

В этих высказываниях хотя бы одно составляющее ложно, и поэтому бабушка сказала неправду.

Конъюнкция – это логическая операция «и», объединяющая высказывания в такое новое высказывание, которое является истинным, если каждое из составляющих истинно, и является ложным, если хотя бы одно из составляющих его высказываний ложно.

Высказывание, полученное при помощи конъюнкции, называется конъюнктивным или соединительным.

Символическая запись соединительн6ого высказывания: А В.

Знаком конъюнкции можно объединить два или более высказываний.

Построим таблицу для уже рассмотренного случая.

Бабушка купила в магазине пряники и конфеты.

№	Высказывание А	Высказывание В	Конъюнкция А В	Истинность (ложность) конъюнкции
1.	Бабушка купила пряники.	Бабушка купила конфеты.	Бабушка купила пряники и конфеты.	И
2.	Бабушка купила пряники.	Бабушка купила макароны.	Бабушка купила пряники и макароны.	Л
3.	Бабушка купила яблоки.	Бабушка купила конфеты.	Бабушка купила яблоки и конфеты.	Л
4.	Бабушка купила яблоки.	Бабушка купила макароны.	Бабушка купила яблоки и макароны.	Л

 

Таблицу истинности можно составить в краткой форме:

№	А	В	АВ
1	и	и	и
2	и	л	л
3	л	и	л
4	л	л	л

 

Примерные задания:

1) Заполните пропуск так, чтобы полученное предложение было

а) истинно;

б) ложно.

Число 15 делится 3 и на...

2)Сформулируйте с помощью союза и утверждения.

а) Белый пушистый снег покрыл все дороги.

б) Сегодня солнечный, теплый день.

 

 

Дизъюнкция высказывания А 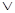В

Т. к. данная тема не входит в минимум содержания обучения, то ее можно дать ученикам в качестве факультатива в 6 классе.

Цель: сформировать понятие дизъюнкции высказывания, научиться применять на практике.

Мотивация: Для того, чтобы дать новое понятие, рассмотрим такую ситуацию.

Турист хочет добраться до Красной площади, но он не знает на чем ему лучше поехать: на метро или на автобусе.

В этом случае возможны 4 случая:

1) Если турист поедет сначала на метро, а затем на автобусе. В этом случае утверждение:

Турист поедет на метро или на автобусе.

является истинным.

2) Если турист поедет на метро, но не поедет на автобусе, то утверждение будет выглядеть так:

Турист поехал на метро или на автобусе.

В этом случае турист все-таки поехал на метро, поэтому утверждение истинно.

3) Если турист поехал на автобусе. В этом случае турист все-таки поехал на автобусе. Утверждение также истинно.

4) Если же турист решил идти пешком, то утверждение будет ложным.

Дадим определение:

Дизъюнкция – это логическая операция «или», объединяющая высказывания в такое новое высказывание, которое является истинным, если хотя бы одно его составляющее является истинным, и является ложным, лишь когда обе его составляющие ложные.

Символическая запись дизъюнктивного объединения: А 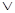 В. Читается А дизъюнкция В.

Знаком дизъюнкции можно объединить два или более высказывания.

Вернемся к высказыванию. Все рассуждения оформим в виде таблицы.

№	Высказывание А	Высказывание В	Дизъюнкция А В	Истинность (ложность) дизъюнкции
1.	Турист поехал на метро.	Турист поехал на автобусе.	Турист поехал на метро или на автобусе.	И
2.	Турист поехал на метро.	Турист не поехал на автобусе.	Турист поехал на метро или не поехал на автобусе.	И
3.	Турист не поехал на метро.	Турист поехал на автобусе.	Турист не поехал на метро или поехал на автобусе.	И
4.	Турист не поехал на метро.	Турист не поехал на автобусе.	Турист не поехал на метро или не поехал на автобусе.	Л

 

Таблицу истинности можно составить в краткой форме.

№	А	В	АВ
1	и	и	и
2	и	л	и
3	л	и	и
4	л	л	л

 

Примерные задания:

1) Заполните пропуск так, чтобы полученное предложение было

а) истинно;

б) ложно.

Число 8 делится 3 или на...

2)Истинно или ложно предложение?

Значение выражения 5-2 равно 3 или 4.

 

Библиографический список

1) Ненашев, М. И.  Введение в логику. М. И. Ненашев // г. Киров. Кировская областная типография, 1997-240с.

2) Дорофеев, Г. В. Математика. 6 класс. Часть 1. Л. Г. Петерсон// М.: «Баласс», «С-инфо», 1998. –С. 112.

3) Дорофеев, Г. В. Математика. 6 класс. Часть 2. Л. Г. Петерсон// М.: «Баласс», «С-инфо», 1999. –С. 128.

4) Дорофеев, Г. В. Математика. 6 класс. Часть 3. Л. Г. Петерсон// М.: «Баласс», «С-инфо», 2002. –С. 176.

5) Дорофеев, Г. В. Математика. 5 класс. Часть 1. Л. Г. Петерсон// М.: «Баласс», «С-инфо», 1996. –С. 176.

6) Дорофеев, Г. В. Математика. 5 класс. Часть 2. Л. Г. Петерсон// М.: «Баласс», «С-инфо», 1997. –С. 240.

7) Ончукова, Л. В. Введение в логику. Логические операции. Л. В. Ончукова // Учебное пособие для 5 класса. – 2-е изд.- Киров: Изд-во ВятГГУ, 2004. – С. 124.

8) Ончукова, Л. В. Элементы логики. Логические операции. Л. В. Ончукова // Учебное пособие для 6 класса.- Киров: Изд-во ВятГГУ, 2002. – С. 88.

9) Игошин, В. И. Математическая логика и теория алгоритмов. В. И. Игошин //Саратов: Изд-во Сарат. ун-та, 1991. – С. 256.

10) Дорофеев, Г. В. Математика. 5 класс. Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова// Под ред. Г. В. Дорофеева, И. Ф. Шарыгина. – 3-е изд.- М.: Просвещение, 2000. –С. 368.

11) Дорофеев, Г. В. Математика. 6 класс. Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова// Под ред. Г. В. Дорофеева, И. Ф. Шарыгина. – 2-е изд.- М.: Дрофа, 1997. –С. 416.

12) Никольская, И. Л. Учимся рассуждать и доказывать. И. Л. Никольская, Е. Е. Семенов // Книга для учащихся 6 – 10 кл. сред. шк.-М.: Просвещение, 1989. –С. 192.

12	Поделиться:

Воспользуйтесь поиском по сайту: