 |
Основные сведения о движении жидкостей
|
|
|
|
Расход Q - объем жидкости в единицу времени; единицы измерения расхода: м3/с, л/с, м3/час, м3/сут. и т.д.
Живое сечение  – площадь поперечного сечения потока, м2.
– площадь поперечного сечения потока, м2.
Смоченный периметр  – суммарная длина стенок поперечного сечения потока, смоченных водой, м.
– суммарная длина стенок поперечного сечения потока, смоченных водой, м.
Гидравлический радиус 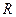 – отношение живого сечения к смоченному периметру
– отношение живого сечения к смоченному периметру
 (2.1)
(2.1)
Уравнение неразрывности записывается в следующем виде:
 (2.2)
(2.2)
где  – скорость движения воды.
– скорость движения воды.
Различают:
- равномерное движение – движение, при котором скорости в различных сечениях потока равны. Установившееся движение – это движение, при котором параметры потока (расход, живое сечение, скорость и т.д.) не изменяются со временем.
При неравномерном движении скорости в различных сечениях отличаются друг от друга. При неустановившемся движении параметры потока изменяются во времени.
Задача 2.1. Для канала (рис. 2.1) определить площадь живого сечения, смоченный периметр и гидравлический радиус.

Рис. 2.1. Схема к задаче
Решение.
Площадь живого сечения равна площади трапеции
 м2
м2
Смоченный периметр равен  =2,7м.
=2,7м.
Гидравлический радиус 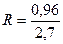 = 0,36м
= 0,36м
Задача 2.2. Определить параметры потока в прямоугольном канале и расход воды. Ширина канала a =2 м, глубина воды в канале h =1 м. Скорость движения воды в канале V =1 м/c.
Решение.
Площадь живого сечения канала w = a х h = 2х1 = 2м2. Смоченный периметр c = 2 h + a = 2х1 + 1 = 3м. Гидравлический радиус R = w/c = 2/3 = 0,667м. Расход воды определяется по формуле Q = w х V = 2х1 = 2м3/с.
Задача 2.3. Для канала, рис.2.1. определить среднюю скорость воды при расходе Q =0,5 м3/с.
Решение.
Из выражения (2.2) V = 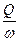 = 0,8/0,96 = 0,83 м/с
= 0,8/0,96 = 0,83 м/с
Задача 2.4. Подобрать диаметр напорного водовода, по которому необходимо пропустить расход 35 л/с. Рекомендуемая скорость 0,8-1 м/с.
|
|
|
Решение.
Площадь живого сечения круглого трубопровода определится по формуле 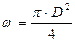 . Из уравнения неразрывности (2.2)
. Из уравнения неразрывности (2.2) 
 = 0,22м. Принимается ближайший стандартный диаметр d = 200 мм. Тогда средняя скорость будет равна V =
= 0,22м. Принимается ближайший стандартный диаметр d = 200 мм. Тогда средняя скорость будет равна V =  =
=  = 1.11 м/c.
= 1.11 м/c.
Уравнение Бернулли
Идеальной жидкостью называют жидкость, которая не сопротивляется касательным напряжениям (не вязкая), таких жидкостей в природе нет, поэтому ее и называют идеальной.
Для реальной жидкости уравнение Бернулли записывается в следующем виде:
 +
+ 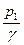 +
+  =
=  +
+  +
+  + hпот (2.3)
+ hпот (2.3)
В уравнении Бернулли  – расстояние от плоскости сравнения до центра тяжести сечения;
– расстояние от плоскости сравнения до центра тяжести сечения;
 - пьезометрическое давление,
- пьезометрическое давление,  - скоростной напор;
- скоростной напор;
hпот - потери напора на участке трубопровода (канала) от сечения 1 до сечения 2.
Из уравнения следует, что при увеличении в трубопроводе или в канале скорости давление падает.
Если в сечениях потока установить скоростную трубку Пито-Прандтля (с изогнутым концом) и пьезометр, то в скоростной трубке вода поднимается на величину пьезометрического и скоростного напора, в пьезометре – только на величину пьезометрического напора.
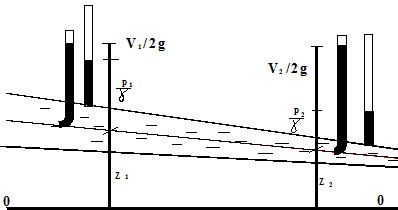
Рис. 2.2. Параметры уравнения Бернулли
Задача 2.5. Определить расход воды, проходящий через водомер Вентури, если перепад показаний пьезометров составляет 20 см, диаметры трубопроводов D1=200мм, D2= 100мм.
Решение.
На схеме рис.2.3. показаны основные параметры задачи. Плоскость сравнения 0-0 проводим через ось потока, сечения располагаем в местах расположения пьезометров. Запишем уравнение Бернулли для заданных сечений:

2.3. Схема водомера Вентури
 +
+ 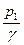 +
+  =
=  +
+  +
+  + hпот
+ hпот
z1 = z2; принимаем потери равными нулю hпот = 0, тогда выражение (2.3) примет вид
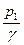 +
+  =
=  +
+  (2.4)
(2.4)
Разница показаний пьезометров  . Выражение (2.4) преобразуется к виду h =
. Выражение (2.4) преобразуется к виду h =  -
-  . Скорость определяется по формуле
. Скорость определяется по формуле 
h = 

Q =  =
= 
 = 0,0162 м3/с = 16,2 л/с
= 0,0162 м3/с = 16,2 л/с
Потери напора
|
|
|
При движении жидкости ее энергия уменьшается за счет потерь на преодоление сопротивлений. Различают потери напора по длине и местные потери напора. Потери напора по длине определяются по формуле Дарси-Вейсбаха:
 (2.5)
(2.5)
где  - коэффициент гидравлического трения;
- коэффициент гидравлического трения;
 - длина трубопровода, м;
- длина трубопровода, м;
 - скорость движения воды, м/с;
- скорость движения воды, м/с;
 - диаметр трубопровода, м;
- диаметр трубопровода, м;
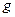 - ускорение свободного падения, м/с2.
- ускорение свободного падения, м/с2.
Потери напора по длине в значительной степени зависят от режима движения. Критерий Рейнольдса, который определяет режим движения, можно найти по формуле:
 (2.6)
(2.6)
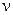 - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.
При значении Re < 2320 движение в потоке относят к ламинарному (струйному), в противном случае говорят о турбулентном движении (вихревом). При ламинарном движении
 (2.7)
(2.7)
При турбулентном движении коэффициент гидравлического трения зависит от двух безразмерных параметров: числа Рейнольдса и относительной шероховатости  ,
,
где  – эквивалентная равномерно-зернистая абсолютная шероховатость, мм.
– эквивалентная равномерно-зернистая абсолютная шероховатость, мм.
Эквивалентная шероховатость принимается по справочным данным. Например, для новых стальных труб эквивалентная шероховатость равна 0,05 мм, для старых – 1 мм.
Коэффициент гидравлического трения при турбулентном движении определяют по формуле Альтшуля:
 (2.8)
(2.8)
Чтобы вычислить потери напора по длине вначале определяют скорость течения, число Рейнольдса Re, а затем коэффициент гидравлического трения.
Потери напора по длине выражают также через расход
 (2.9)
(2.9)
где S – полное гидравлическое сопротивление (м с2/л2), определяется
 (2.10)
(2.10)
So - удельное гидравлическое сопротивление линии, зависит от материала труб и диаметра; для неновых металлических и пластмассовых труб приводится в приложении 4;
 - коэффициент, учитывающий неквадратичность зависимости потерь напора от средней скорости движения воды V, м/с; для металлических труб при скорости V
- коэффициент, учитывающий неквадратичность зависимости потерь напора от средней скорости движения воды V, м/с; для металлических труб при скорости V  1,2м/с
1,2м/с  =1;
=1;
при меньшей скорости  определяется по формуле
определяется по формуле
 =
=  (2.11)
(2.11)
для пластмассовых труб  =
=  (2.12)
(2.12)
Задача 2.6. Определить потери напора по длине в новом стальном трубопроводе диаметром 200мм и длиной 400м. По трубопроводу пропускается вода с температурой 10оС, расход воды 38 л/с.
Решение.
Определяется скорость движения воды в трубопроводе
|
|
|
 1,21 м/с
1,21 м/с
Из приложения 1 эквивалентная шероховатость – 0.5 мм; из приложения 2 кинематическая вязкость ν =1.31*10-6. Вычисляется значение критерия Рейнольдса
Re =  =
=  = 184732
= 184732
Коэффициент гидравлического трения определяется по формуле (2.8)
 = 0.044
= 0.044
Для определения потерь напора используется формула Дарси-Вейсбаха
 = 6,57 м
= 6,57 м
Задача 2.7. Определить потери напора по длине в трубопроводе из полиэтиленовых труб диаметром 110мм и длиной 400м. По трубопроводу пропускается расход воды 8 л/с.
Решение.
Определяется скорость движения воды в трубопроводе
 0,84 м/с
0,84 м/с
Вычисляется коэффициент, учитывающий неквадратичность зависимости потерь напора от средней скорости движения воды V, м/с для пластмассовых труб по формуле (2.12)  =
=  =
=  = 1,04. Из приложения 4 для трубопровода диаметром 110мм удельное сопротивление S0=323.9х10-6. Потери напора вычисляются по формуле (2.9) с учетом формулы (2.10)
= 1,04. Из приложения 4 для трубопровода диаметром 110мм удельное сопротивление S0=323.9х10-6. Потери напора вычисляются по формуле (2.9) с учетом формулы (2.10)
hд = 323,9·10-6· 400 ·1,04· 82 = 8,97 м.
Местными потерями напора называют потери напора, сосредоточенные на коротких участках потока, обусловленные изменением направления движения потока воды (скорости), потери в арматуре (задвижке, вентиле, кране и др.), при соединении или разделении потоков, при сужении или расширении сечения трубы (канала), при поворотах.
Местные потери напора определяют по формуле Вейсбаха:
 (2.13)
(2.13)
ζ - коэффициент местного сопротивления, принимается по справочным данным; выборочно приведен в приложении 3.
Порядок вычисления местных сопротивлений: определяют скорость течения воды в трубопроводе или канале, как правило, после сопротивления (поворот, сужение, расширение трубопровода или канала), по значению отношения площади сечения или угла поворота определяют значение коэффициента местных сопротивлений, а затем подсчитывают величину местного сопротивления.
Общие потери напора в трубопроводе
 (2.14)
(2.14)
Потери напора по длине и местные потери определяются в метрах водного столба.
В зависимости от длины и диаметра трубопровода различают «длинные» и «короткие» трубопроводы. Если местные потери незначительны по сравнению с потерями напора по длине (Σhм < Σhдл), то такие трубопроводы воды считаются «длинными»; суммарные потери напора в них принимаются на 5-10% больше потерь напора по длине
|
|
|
 (2.15)
(2.15)
В гидравлически коротких трубопроводах местные сопротивления сравнимы по величине с местными потерями напора, в этих трубопроводах общие потери напора определяют по формуле (2.14).
Задача 2.8. Определить глубину слоя воды в резервуаре при следующих исходных данных: Расход воды q = 24 л/с. Длины трубопроводов L1 = 100 м, L2= 50 м. Диаметры D1=150 мм, D2 = 100 мм. Вода из трубопровода через задвижку (полностью открытая) изливается в атмосферу. Трубы стальные. Температуру воды принять 10 оС.
Решение.
Для решения задачи необходимо воспользоваться уравнением Бернулли. Плоскость сравнения проведем через ось потока. Сечение 1-1 и 2-2 в начале и в конце системы. Уравнение Бернулли имеет вид:
 +
+ 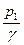 +
+  =
=  +
+  +
+  + hпот
+ hпот
В сечениях 1-1 и 2-2 давление атмосферное, поэтому 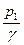 =
=  . Так как плоскость сравнения проходит через ось потока
. Так как плоскость сравнения проходит через ось потока  =0,
=0,  =H.
=H.

Рис. 2.4. Резервуар и система трубопроводов
После такой замены уравнение примет вид
Н +  =
=  + hпот
+ hпот
При известных диаметрах и расходах скорости движения воды будут равны:
 1,36м/с
1,36м/с
 3,06 м/с
3,06 м/с
Скоростные напоры соответственно равны:
 =
=  = 0,09
= 0,09  =
=  = 0,48
= 0,48
Н + 0,09 = 0,48 + hпот → Н = (0,48 - 0,09) + hпот = 0,39 + hпот
Потери напора в данном случае складываются из потерь напора по длине на участках трубопровода L1 и L2 из местных потерь напора: вход в трубу, резкое сужение, задвижка.
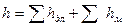 =
=  +
+  +
+ 
Коэффициенты местных сопротивлений ξ определяются из приложения 5:
ξвх= 0,5; ξзад = 0,12
ξсуж=  или ξсуж=
или ξсуж=  =
=  = 0.225.
= 0.225.
Чтобы вычислить потери напора по длине предварительно определяются:
- число Рейнольдса (коэффициент кинематической вязкости  принимается по приложению 1,
принимается по приложению 1,  =1.31*10-6. шероховатость kэ принимается по приложению 2, kэ=0.5 мм);
=1.31*10-6. шероховатость kэ принимается по приложению 2, kэ=0.5 мм);
Re1 =  =
=  = 155725 Re2 =
= 155725 Re2 =  =
=  = 233588
= 233588
- коэффициент гидравлического трения
 =
=  = 0,027
= 0,027
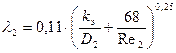 =
=  = 0,030
= 0,030
Тогда суммарные потери в трубопроводах
 =
= 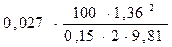 +
+  +
+  =
=
= 9,11(м)
 =9,11 м; Н = 0,39 + 9,11 = 9,5 (м)
=9,11 м; Н = 0,39 + 9,11 = 9,5 (м)
|
|
|


