Основные физические свойства

Основные механические характеристики

 

Плотностью жидкости называют массу жидкости заключенную в единице объема.

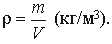
Удельным весом называют вес единицы объема жидкости, который определяется по формуле:

С увеличением температуры удельный вес жидкости уменьшается.

Основные физические свойства

1. Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия, который определяется по формуле

где V - первоначальный объем жидкости,
dV - изменение этого объема, при увеличении давления на величину dP.

Величина обратная βV называется модулем объемной упругости жидкости:

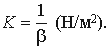
2. Температурное расширение - относительное изменение объема жидкости при увеличении температуры на 1°С при Р = const. Характеризуется коэффициентом температурного расширения

3. Сопротивление растяжению. Особыми физическими опытами было показано, что покоящаяся жидкость (в частности вода, ртуть) иногда способна сопротивляться очень большим растягивающим усилиям. Но в обычных условиях такого не происходит, и поэтому считают, что жидкость не способна сопротивляться растягивающим усилиям.

4. Силы поверхностного натяжения - эти силы стремятся придать сферическую форму жидкости.

5. Вязкость жидкости - свойство жидкости сопротивляться скольжению или сдвигу ее слоев. Суть ее заключается в возникновении внутренней силы трения между движущимися слоями жидкости, которая определяется по формуле Ньютона

где S - площадь слоев жидкости или стенки, соприкасающейся с жидкостью, м²,
μ- динамический коэффициент вязкости, или сила вязкостного трения,
d /dy - градиент скорости, перпендикулярный к поверхности сдвига.

Отсюда динамическая вязкость равна

где τ - касательные напряжения жидкости, τ = T/S.

6. Пенообразование. Выделение воздуха из рабочей жидкости при падении давления может вызвать пенообразование.

7. Химическая и механическая стойкость. Характеризует способность жидкости сохранять свои первоначальные физические свойства при эксплуатации и хранении.

8. Совместимость. Совместимость рабочих жидкостей с конструкционными материалами и особенно с материалами уплотнений имеет очень большое значение. 9. Испаряемость жидкости. Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий в которых она находится: от температуры, от площади испарения, от давления, и от скорости движения газообразной среды над свободной поверхностью жидкости (от ветра).

10. Растворимость газов в жидкостях характеризуется объемом растворенного газа в единице объема жидкости и определяется по закону Генри:

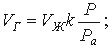
где V_Г - объем растворенного газа; V_Ж - объем жидкости; k - коэффициент растворимости; Р - давление; Р_а - атмосферное давление.

1. Основные уравнения гидростатики.

P = P₀ + ρ gh = P₀ + hγ

где р1 – абсолютное давление, Па;

рo – давление на свободную поверх- ность, Па;

ρ – плотность, кг/м3;

g – ускорение свободного падения, м/с 2;

h – глубина погружения, м.

1. Сила гидростатического давления на плоские и кривые стенки

Fж = ρg (H₀ +h_c)S = P_cS, (3.12)

Полная сила давления жидкости Fж на плоскую стенку равна произведению площади стенки S на гидростатическое давление Р_с в центре тяжести этой площади.

1.В частном случае, когда давление Р₀ является атмосферным и действует также с другой стороны стенки, сила F_{изб ж} избыточного давления жидкости на плоскую стенку равна лишь силе Fж давления от веса жидкости, т. е.

Fизб ж =Fж = P_cS= ρgh_cS.

2. В общем случае давление Р₀ может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку 6удем рассматривать как сумму двух сил: F₀ от внешнего давления Р₀ и силы Fж от веса жидкости, т. е.

F= F₀ + Fж = (P₀+Pс)S. (3.13.)

 

1. Закон Паскаля, закон Архимеда.

Закон Архимеда о подъёмной (архимедовой) силе Fn, действующей на погружённое в жидкость тело, имеет вид

Fn = g Vт

где g — удельный вес жидкости;

Vm — объём жидкости, вытесненной телом.

Закон Паскаля звучит так: внешнее давление, приложенное к жидкости, находящейся в замкнутом резервуаре, передаётся внутри жидкости во все её точки без изменения.

1. Виды движения

Основные виды движения жидкости:

· равномерное и неравномерное;

· установившееся и неустановившееся;

· напорное и открытое (безнапорное); Напорным называется движение жидкости со всех сторон ограниченное твердыми стенками. Безнапорное - часть периметра жидкости не ограничено твердыми стенками, т.е. имеется свободная поверхность.

 

1. Виды потоков, режимов.

различают два основных режима движения: ламинарный и турбулентный. Ламинарным называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь. Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.

Турбулентным называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом.

Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока

, (82)

где 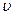– скорость, м/сек; R - гидравлический радиус, м; v - кинематический коэффициент вязкости, м2/сек.

Это отношение называется числом Рейнолъдса. Значение числа Re, при котором турбулентный режим переходит в ламинарный, называют критическим числом Рейнолъдса ReKp.

Если фактическое значение числа Re, вычисленного по формуле (82), будет больше критического Re > ReKp – режим движения турбулентный, когда Re < ReKp – режим ламинарный.

 

 

1. Уравнение неразрывного потока и постоянства расхода.

Учитывая, что 1. проникновение жидкости через боковую поверхность невозможно (т.к. поверхность образована линиями тока) 2. жидкость несжимаема 3. жидкость является сплошной средой (отсутствуют разрывы) можно записать

u1dω 1dt = u2dω 2dt Q = const

u1/u2 = dω 2/dω 1 v1/v2 = ω 2 / ω 1

1. Уравнение Бернулли.
2. Потери напора по длине

При равномерном движении в трубах потери напора по длине, как при турбулентном, так и при ламинарном движении определяются для круглых труб по формуле Дарси

(3.11)

а для труб любой другой формы сечения по формуле

(3.12)

В некоторых случаях также используют формулу

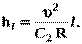(3.13)

Потери давления на трение по длине , Па, определяются по формуле

(3.14)

где ─ длина участка трубы или канала, м;

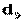─эквивалентный диаметр, м;

─средняя скорость течения, м/с;

─гидравлический радиус трубы, м;

─коэффициент гидравлического трения;

─коэффициент Шези, связанный с коэффициентом гидравлического трения зависимостями

 

1. Что такое напор.

Гидродинамический напор H (м) — это энергетическая характеристика движущейся жидкости. Понятие гидродинамического напора в гидравлике имеет фундаментальное значение.

Гидродинамический напор H (рис. 11) определяется по формуле:

(20)

где z — геометрический напор (высота), м; hp — пьезометрический напор (высота), м; hV = V 2 / (2 g) — скоростной напор, м; V — скорость потока, м/c; g — ускорение свободного падения, м 2 /с.

 

1. Уравнение Шизи. Безнапорные потоки.

 

1. Гидравлический удар.

Поделиться:

Воспользуйтесь поиском по сайту: