 |
Схема расположения полей допусков
|
|
|
|
Отклонения отверстия и вала по ГОСТ 25347-82
ЕS=+0.027мм еs= 0мм
ЕI=-0,027мм еi= -0,054мм
Схема расположения полей допусков
1. Предельные размеры:
Dmax = N+ ES= 95+0,027=95,027 мм
Dmin = N + EI =95-0,027=94,973 мм
dmax = N + еs =95+0=95мм
dmin = N + ei =95-0,054=94,946мм
2. Допуски отверстия и вала:
ТD = Dmax – Dmin =95,027-94,973=0,054 мм
Тd = dmax – dmin =95-94,946=0,054мм
3. Зазоры:
Smax = Dmax – dmin =95,027-94,946=0,081мм
Imax= dmax-dmin = 95- 94.973=0,027мм
4. Средний зазор:
Sc = (Smax +Imin)/2 = (0.081-0.027)/2=0.027 мм.
5. Допуск зазора (посадки):
Тs = ТD + Тd = 0.054+0.054=0.108мм
6. Обозначение предельных отклонений размеров на конструкторских чертежах:
| а) условное обозначение полей допусков: |
| б) числовые значения предельных отклонений: | |
| в) условное обозначение полей допусков и числовых значений предельных отклонений: |
7. Обозначение размеров на рабочих чертежах:
8.Расчет калибров для проверки итверстия и вала
а)Для калибров пробок
z=0.008 y=0.006 H=0.006
б)для калибр скоб
z=0.008 y=0.006 H=0,01
Калибр для проверки отверстия
Пробка ПР
Исполнительный размер пробки:
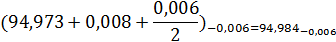
Средневероятный износ:
Износ рабочим:
94,973-0,006+0,3*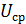 
=94,973-0,006+0,0042=94,9712мм
Износ цеховым контролером:
94,973-0,006=94,967мм
Непроходная сторона:
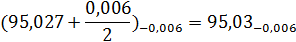
Калибр для проверки вала
Скоба ПР
Исполнительный размер скобы ПР:
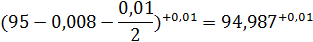
Средневероятный износ:
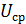=0,008+0,006=0,014*0,3=0,0042мм
Износ рабочим:
95+0,006-0,3* 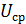=95+0,006-0,3*0,014=950,018мм
Износ цеховым контролером:
95+0,006=95,006мм
Непроходная сторона:
Задание.
Рассчитать параметры посадки ÆH7/f7; написать все виды обозначения предельных отклонений размеров на конструкторских и рабочих чертежах; рассчитать калибры для проверки отверстия и вала заданной посадки; дать рабочие чертежи калибров.
|
|
|
Для расчета дана посадка c зазором
Отклонения отверстия и вала по ГОСТ 25347-82
ЕS=+0.03мм еs= -0,03мм
ЕI= 0 мм еi= -0,06мм
Схема расположения полей допусков
1. Предельные размеры:
Dmax = N+ ES= 55+0,03=55,03мм
Dmin = N + EI = 55 + 0= 55 мм
dmax = N + еs = 55-0,03=54,97 мм
dmin = N + ei = 55-0,06=54,94 мм
2. Допуски отверстия и вала:
ТD = Dmax – Dmin = 55,03-55=0,03 мм
Тd = dmax – dmin = 54,97-54,94=0,03мм
3. Зазоры:
Smax = Dmax – dmin = 55,03-54,94=0,09мм
Smin = Dmin - dmax = 55-54,97=0,03мм
4. Средний зазор:
Sc = (Smax + Smin)/2 = (0,09+0,03)/2= 0,06мм.
5. Допуск зазора (посадки):
Тs = ТD + Тd = 0,03+0,03=0,06 мм
6. Обозначение предельных отклонений размеров на конструкторских чертежах:
| а) условное обозначение полей допусков: |
| б) числовые значения предельных отклонений: |
| в) условное обозначение полей допусков и числовых значений предельных отклонений: |
7. Обозначение размеров на рабочих чертежах:
8.Расчет калибров для проверки отверстия и вала
а)Для калибров пробок
z=0.004 y=0.003 H=0.005
б)для калибр скоб
z=0.004 y=0.003 H=0,005
Калибр для проверки отверстия
Пробка ПР
Исполнительный размер пробки:
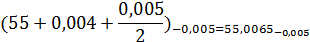
Средневероятный износ:
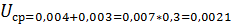
Износ рабочим:
55-0,003+0,3* 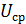=55-0,003+0,0021=54,9991мм
Износ цеховым контролером:
55-0,003=54,997мм
Непроходная сторона:
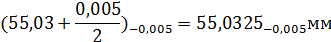
Калибр для проверки вала
Скоба ПР
Исполнительный размер скобы ПР:
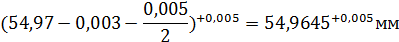
Средневероятный износ:
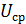=0,004+0,003=0,007*0,3=0,0021мм
Износ рабочим:
54,97+0,003-0,3* 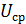=54,97+0,003-0,3*0,007=54,9709мм
Износ цеховым контролером:
54,97+0,003=54,973мм
Непроходная сторона:
2 ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ
В таблице 2.1 приведены 100 независимых числовых значений результата измерений напряжения U цифровым вольтметром, каждое из которых повторилось m раз. Определить значение измеряемого напряжения.
|
|
|
Таблица 2.1
Решение:
1 Используя полученные данные, найдем значение среднего арифметического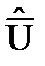 
и оценки среднего квадратического отклонения Su:
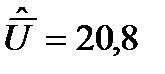В; 
В.
2 С помощью правила «трех сигм» проверим наличие грубых промахо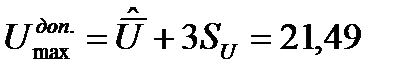в:
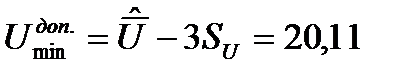В
В
Ни один из результатов не выходит за границы интервала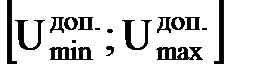 
, следовательно, с вероятностью 0.134 принимается гипотеза об отсутствии грубых промахов.
3 Предположим, что вероятность результата измерений подчиняется нормальному закону. Проверим правдивость этой гипотезы с помощью критерия Пирсона. Все расчеты сведем в таблицу 2.2.
4 Определим значение аргумента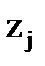 
интегральной функции нормированного нормального распределения:
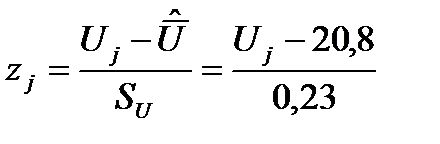
Таблица 2.2
Расчет критерия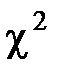 
Пирсона
| i | Интервалы |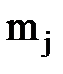 
| 
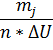
| tj-1 | tj | Фj-1 | Фj | Pj |  =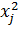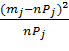 
| |
| 
| |||||||||
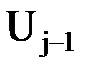
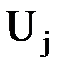
| 20,30 | 20,4 | 0,4 | -2,2 | -1,3 | -0.4868 | -0.4032 | 0.0836 | |||
| 20,4 | 20,5 | 0,4 | -2,2 | -1,3 | -0,4868 | -0,4032 | 0.0836 | |||
| 20,5 | 20,6 | -1,3 | -0.8 | -0.4032 | -0.2881 | 0.1151 | ||||
| 20,6 | 20,7 | 1,4 | -0.8 | -0,4 | -0.2881 | -0.1554 | 0.1327 | |||
| 20,7 | 20,8 | 2.3 | -0,4 | -0.1554 | 0.1554 | |||||
| 20,8 | 20,9 | 1.1 | 0.4 | 0.1554 | 0.1554 | |||||
| 20,9 | 1,5 | 0.4 | 0,8 | 0.1554 | 0.2881 | 0.1327 | ||||
| 21,1 | 0,8 | 1,3 | 0.2881 | 0.4032 | 0.1151 | |||||
| 21,1 | 21,2 | 0,2 | 1,3 | 2,6 | 0.4032 | 0.4953 | 0,0921 | |||
| 21,2 | 21,3 | 0,2 | 1,3 | 2,6 | 0,4032 | 0.4953 | 0,0921 | |||
| 21,30 | 21,4 | 0,2 | 1,3 | 2,6 | 0,4032 | 0.4953 | 0,0921 | |||
a. По последнему столбцу рассчитаем значение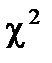 
-критерия:
.
b. Определим табличное (критическое) значение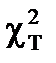 
-критерия Пирсона, задавшись доверительной вероятностью, равной 0,97 и вычислив по формуле число степеней свободы:
r = 8 – 3 = 5
; 
.
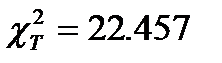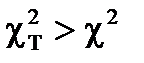Таким образом, с вероятностью 0,92 гипотеза о нормальности закона распределения вероятности результата измерений напряжения принимается.
5 Представим результаты в виде доверительного интервала с доверительной вероятностью Р = 0,92.
a. Для этого определим среднее квадратическое отклонение среднего арифметического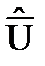 
значения напряжения по формуле:
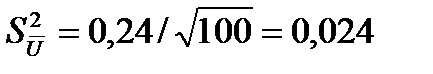В
b. Исходя из того, что закон распределения вероятности результата измерения с вероятностью 0,92 соответствует нормальному, считаем, что, и закон распределения вероятности среднего арифметического тоже соответствует нормальному. Поэтому выбираем параметр t по таблице нормированного нормального распределения вероятности. Для доверительной вероятности Р=0.92 параметр t=2.18
|
|
|
Тогда результат измерения запишется следующим образом:
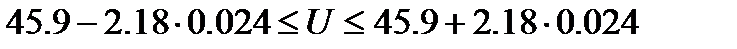
или с вероятностью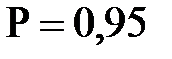 
.
45.8476 В ≤ U ≤ 45.95232 В
Учитывая то обстоятельство, что среднее квадратическое отклонение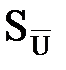 
может быть оценено экспериментально с точностью до двух значащих цифр, округлим границы доверительного интервала до тысячных долей вольта. В итоге получим:
45.848 В ≤ U ≤ 45.952 В
Если же есть основания полагать, что среднее арифметическое 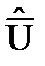имеет неизвестное, отличное от нормального распределение вероятности, то относительную ширину доверительного интервала рассчитаем по формуле:
, 
.
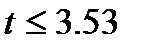Окончательно результат измерения примет вид (см. формулу (2.17)):
или с вероятностью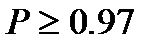 
или после округления
6 Строим саму гистограмму (рис.2.1).
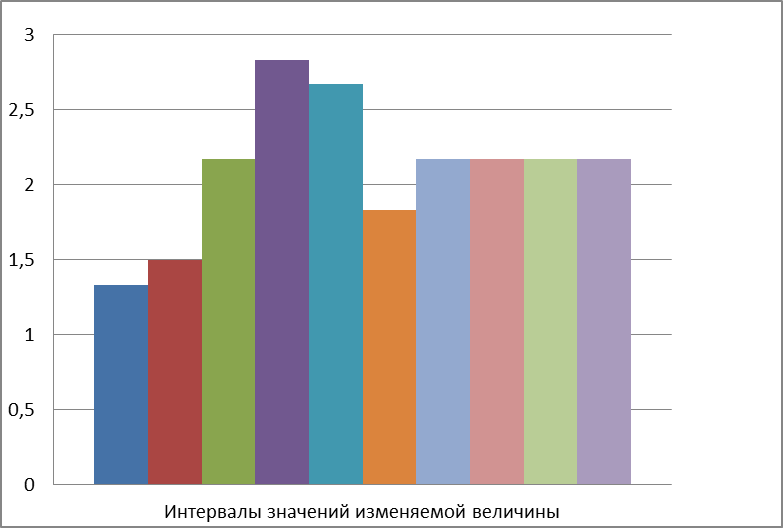
Рисунок 2.1. Гистограмма и выравнивающая нормальная кривая, иллюстрирующая гипотезу о виде ЗРВ
|
|
|
