Расчёт множественных коэффициентов корреляции

РЕАЛИЗАЦИЯ ЗАДАЧ МНОГОМЕРНОГО КОРРЕЛЯЦИОННОГО АНАЛИЗА

С ИСПОЛЬЗОВАНИЕМ ПАКЕТА MS EXCEL

 

Проведение корреляционного анализа рассмотрим на примере.

С целью анализа взаимосвязи показателей эффективности производства продукции бы­ли рассмотрены параметры производственно-хозяйственной деятельности 30 предприятий машиностроения.

Необходимо провести анализ взаимосвязи следующих экономических показателей:

Результативный признак:

Y₁ – производительность труда

Факторные признаки:

Х₁₀ - фондоотдача;

Х₁₄ - фондовооруженность труда;

Х₁₅ - оборачиваемость нормируемых оборотных средств;

X₁₆ - оборачиваемость ненормируемых оборотных средств.

Исходные данные представлены в файле Коррел. анализ.xls.

Предположим, что рассматриваемые признаки Y₁, Х₁₀, Х₁₄, Х₁₅, X₁₆ в генеральной совокупности подчиняются нормальному закону распределения, и указанные данные представляют выбор­ку из этой генеральной совокупности. Для решения данной задачи воспользуемся программным продуктом MS EXCEL.

1. Скопируйте в свою папку или на Рабочий стол файл Коррел. анализ.xls с диска U:\Общая информация\Эконометрика;

2. Откройте файл Коррел. анализ.xls иперейдите на лист Задание;

3. Подключите в Excel пакет анализа:

Меню СЕРВИС – Надстройки – Пакет анализа – ОК;

Меню СЕРВИС – Анализ данных – Корреляция – ОК;

4. Укажите следующие параметры диалогового окна «Корреляция»:

1. Входной интервал

Укажите массив исходных показателей, выделив мышкой все значения ис­следуемых переменных (Y₁, Х₁₀, Х₁₄, Х₁₅, X₁₆).

2. Группирование

Установите переключатель в положение по столбцам.

Метки в первой строке

Поставьте флажок в опции Метки в первой строке, чтобы добавить во входной диапазон верхнюю строку, содержащую названия переменных, тогда корреляци­онная матрица будет выведена с названиями переменных.

Выходной интервал

Поставьте точку в опции Выходной интервал, затем щелкните мышью в строке напротив надписи Выходной интервал и щелкните мышью в ячейку G1 листа Задание.

После установки указанных параметров нажмите на кнопку ОК.

 

Получим корреляционную матрицу в следующем виде:

Таблица 1

 

	Y1	X10	Х14	Х15	X16
Y1
X10	-0,02152
Х14	0,577299	-0,03604
Х15	0,334637	0,153663	0,077981
X16	-0,2042	-0,34832	-0,16676	-0,25017

 

5. Для дальнейших расчётов необходимо привести корреляционную матрицу к обычному виду, заполнив верхний треугольник таблицы. При этом надо учесть, что матрица парных коэффициентов корреляции является симметричной, и коэффициенты r_ij = r_ji. Скопируйте нужные парные коэффициенты корреляции в соответствующие ячейки.

В результате мы получим матрицу парных коэффициентов корреляции размерности 5x5:

Таблица 2

	Y1	X10	Х14	Х15	X16
Y1		-0,02152	0,577299	0,334637	-0,2042
X10	-0,02152		-0,03604	0,153663	-0,34832
Х14	0,577299	-0,03604		0,077981	-0,16676
Х15	0,334637	0,153663	0,077981		-0,25017
X16	-0,2042	-0,34832	-0,16676	-0,25017

6. Далее необходимо проверить значимость полученных коэффициентов корреляции, т.е. гипотезу Hо: r_ij = 0. Для этого рассчитаем наблюдаемые значения t -статистики для всех ко­эффициентов корреляции по формуле:

Для этого скопируйте предыдущую таблицу и вставьте ее под самой собой, отступив две строки. Удалите из таблицы все числовые данные и установите курсор в ячейку на пересечении переменных Y₁ и Х_10. Находясь в указанной ячейке, введите в строку формул выражение для записи вышеуказанной формулы в следующем виде:

=(H3/КОРЕНЬ(1-H3*H3))*КОРЕНЬ(49).

При вводе данного выражения необходимо щелкать мышью в ячейку с соответствующим коэффициентом, для которого рассчитывается значение t -статистики, в данном случае в ячейку H3. Введя указанное выражение, нажмите ENTER. Растяните введенную формулу с помощью черного крестика по соседним ячейкам, в результате у вас должна получиться следующая матрица наблюдаемых значений t -статистики:

Таблица 3

tнабл	Y1	X10	Х14	Х15	X16
Y1
X10	-0,15071
Х14	4,949094	-0,25242
Х15	2,485769	1,088567	0,547536
X16	-1,4602	-2,60115	-1,18391	-1,80872

 

Мы вычислили наблюдаемые значения t -статистики только для нижнего треугольника таблицы, поскольку матрица парных коэффициентов корреляции является симметричной.

7. Наблюдаемые значения t -статистик необходимо сравнить с критическим значением t_кр, найденным для уровня значимости α=0,05 и числа степенен свободы ν =п-2. Для этого используем встроенную функцию Excel ВСТАВКА – Функция – Статистические – СТЬЮДРАСПОБР.

Для расчета t_кр выделите пустую ячейку, затем вызовите функцию СТЬЮДРАСПОБР, введите в поле Вероятность число 0,05, а в поле Степени_свободы – число 49, поскольку всего мы имеем 51 наблюдение, поэтому ν =п-2=51-2=49. Нажав на кнопку ОК, мы получим следующее значение t_кр = 2,009574.

Сравним рассчитанные нами наблюдаемые значения t -статистики с критическим (табличным) и опреде­лим, какие коэффициенты значимы, а какие нет. Коэффициент значим, если его | t_набл | > t_кр.

8. Отметьте жирным шрифтом в таблице значимые коэффициенты корреляции:

Таблица 4

Матрица парных коэффициентов корреляции исследуемых показателей с выделением зна­чимых коэффициентов (при α=0,05)

 

 

	Y1	X10	Х14	Х15	X16
Y1		-0,02152	0,577299	0,334637	-0,2042
X10	-0,02152		-0,03604	0,153663	-0,34832
Х14	0,577299	-0,03604		0,077981	-0,16676
Х15	0,334637	0,153663	0,077981		-0,25017
X16	-0,2042	-0,34832	-0,16676	-0,25017

9. Для значимыхпарных коэффициентов корреляции построим с заданной надёжностью γ=0,95 интервальную оценку r_min< r < r_тах с помощью Z-преобразования Фишера (см. формулы в лекции). Z' можно найти, используя функцию Excel:

ВСТАВКА – Функция – Статистические – ФИШЕР, в качестве аргумента вводится значение соответствующего выборочного коэффициента корреляции r.

10. Значение t_γ рассчитаем, используя функцию Excel: ВСТАВКА – Функция – Статистические – НОРМСТОБР, где в поле Вероятность вводится значение 0,95.

Z_min = 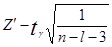; Z_max =

Для обратного преобразования используем функцию Excel: ВСТАВКА – Функция – Статистические –ФИШЕРОБР, где в поле Y вводятсяячейки со значением Z_min, Z_max, т.е. для расчета r_min вводим Z_min, а для расчета r_тах вводим Z_max.

Расчеты представим в виде следующей таблицы:

Таблица 5

Расчёт доверительных интервалов для парных генеральных коэффициентов корреляции ис­следуемых экономических показателей с надёжностью γ = 0,95

	r	Z’	Zmin	Zmax	rmin	rтах
Y1X14	0,577299	0,658403	0,413403	0,903403	0,3913583	0,71795081
Y1X15	0,334637	0,348041	0,103041	0,593041	0,10267786	0,5320792
Х10Х16	-0,34832	-0,36353	-0,60853	-0,11853	-0,5430915	-0,11797801

Таким образом, доверительные интервалы с надёжностью γ = 0,95найдены для всех значимых парных коэффициентов корреляции.

По полученным данным можно сделать следующие выводы:

Между исследуемыми показателями выявлены значимые корреляционные зависимости.

1). Значимая обратная корреляционная взаимосвязь обнаружена между изучаемым при­знаком Х₁₀ - фондоотдача и факторным признаком X₁₆ - оборачиваемость ненормируемых оборотных средств.

2). Между производительностью труда (Y₁) и фондовооруженностью труда (Х₁₄) имежду производительно­стью труда (Y₁) иоборачиваемостью нормируемых оборотных средств (Х₁₅) существует прямая связь.

3). Наиболее сильная связь существует между результативным признаком производительность труда (Y₁) и факторным признаком фондовооруженность труда (Х₁₄), причем отмеченная связь прямая.

Расчёт частных коэффициентов корреляции. Сравнение частных и парных коэф­фициентов корреляции.

 

Частные коэффициенты корреляции характеризуют взаимосвязь между двумя выбран­ными переменными при исключении влияния остальных показателей (т.е. характеризуют «чистую» связь только между этими признаками) и важны для понимания взаимодействия всего комплекса показателей, т.к. позволяют определить механизмы усиления-ослабления влияния переменных друг на друга.

Частный коэффициент (k-2)- гo порядка между переменными, например, между Y₁ и Х₁₀, равен:

,

где R_ij - алгебраическое дополнение элемента r_ij корреляцион­ной матрицы R, равное , где M_ij – минор-определитель матрицы, полученный из матрицы R путем вычеркивания i- той строки и j- го столбца.

11. Для расчета частных коэффициентов корреляции нужно сформировать в Excel соответст­вующие матрицы размерности 4*4.

 

Например, алгебраическое дополнение R₁₂ рассчитывается путем вычеркивания из нашей корреляционной матрицы первой строки и второго столбца:

 

	Y1	X10	Х14	Х15	X16
Y1		-0,02152	0,577299	0,334637	-0,2042
X10	-0,02152		-0,036036	0,153663	-0,34832
Х14	0,577299	-0,03604		0,077981	-0,16676
Х15	0,334637	0,153663	0,077981		-0,25017
X16	-0,2042	-0,34832	-0,166761	-0,25017

 

-0,02152	-0,036036	0,153663	-0,34832
0,577299		0,077981	-0,16676
0,334637	0,077981		-0,25017
-0,2042	-0,166761	-0,25017

 

 

 

Аналогично

	-0,036036	0,153663	-0,34832
-0,03604		0,077981	-0,16676
0,153663	0,077981		-0,25017
-0,34832	-0,166761	-0,25017

 

 

	0,577299	0,334637	-0,2042
0,577299		0,077981	-0,16676
0,334637	0,077981		-0,25017
-0,2042	-0,166761	-0,25017

 

 

 

Чтобы найти определители этих матриц используем функцию Excel: ВСТАВКА - Функция - Математические - МОПРЕД (указать в качестве массива соот­ветствующую матрицу переменных). Воспользовавшись функцией получаем:

-(-0,05438)

0,786557

0,528443

Подставив значения в формулу, получаем = - 0,084348

Аналогично проводятся расчеты для всех остальных частных коэффициентов корреляции:

R₁₃=(-1)¹⁺³ * M₁₃ = - 0,42585 R₃₄=(-1)³⁺⁴ * M₃₄ = - (-0,1)

R₁₄=(-1)¹⁺⁴ * M₁₄ = - 0,225305 R₃₅=(-1)³⁺⁵ * M₃₅ = 0,063223

R₁₅=(-1)¹⁺⁵ * M₁₅ = 0,05218 R₄₅=(-1)⁴⁺⁵ * M₄₅ = - (-0,08965)

R₂₃=(-1)²⁺³ * M₂₃ = - (-0,02282) R₃₃=(-1)³⁺³ * M₃₃ = 0,702903

R₂₄=(-1)²⁺⁴ * M₂₄ = - 0,05483 R₄₄=(-1)⁴⁺⁴ * M₄₄ = 0,551944

R₂₅=(-1)²⁺⁵ * M₂₅ = - (-0,18526) R₅₅=(-1)⁵⁺⁵ * M₅₅ = 0,561651

 

r_13/245 = 0,572722 r_25/134 = - 0,340055

r_14/235 = 0,341947 r_34/125 = - 0,160548

r_15/234 = - 0,078507 r_35/124 = - 0,100622

r_23/145 = - 0,037443 r_45/123 = - 0,161016

r_24/135 = 0,101525

В результате получим матрицу следующего вида:

Таблица 6 Матрица частных коэффициентов корреляции исследуемых экономических показателей

 

	Y1	X10	Х14	Х15	X16
Y1		- 0,084348	0,572722	0,341947	- 0,078507
X10	- 0,084348		- 0,037443	0,101525	- 0,340055
Х14	0,572722	- 0,037443		- 0,160548	- 0,100622
Х15	0,341947	0,101525	- 0,160548		- 0,161016
X16	- 0,078507	- 0,340055	- 0,100622	- 0,161016

 

12. Далее необходимо проверить значимость полученных частных коэффициентов корреля­ции. Для этого рассчитаем наблюдаемые значения t -статистик для всех коэффициентов по формуле:

где l - порядок частного коэффициента корреляции, совпадающий с количеством фиксируе­мых переменных случайных величин (в нашем случае l =3),

n - количество наблюдений.

Построим матрицу наблюдаемых значений t -статистик для всех коэффициентов r_ij:

Таблица 7

Матрица наблюдаемых значений t-статистик для частных коэффициентов корреляции исследуе­мых экономических показателей

tнабл	Y1	X10	Х14	Х15	X16
Y1
X10	-0,574122
Х14	4,7385072	-0,254129
Х15	2,4679682	0,692152	-1,103200
X16	-0,534109	-2,452522	-0,685933	-1,106502

 

 

Наблюдаемые значения t -статистик необходимо сравнить с критическим значением t_кр, най­денным для уровня значимости α =0,05 и числа степеней свободы v=n-l-2.

Для этого используем встроенную статистическую функцию Excel СТЬЮДРАСПОБР, введя в диалоговое окно функции вероятность α =0,05 и число степеней свободы v=n-l-2=51-3-2=46.

13. Сравним расчетные значения с критическим и определим, какие коэффициенты значимы. По­лучим матрицу частных коэффициентов корреляции с выделенными значимыми коэффициента­ми:

Таблица 8

Матрица частных коэффициентов корреляции исследуемых показателей с выделением значи­мых коэффициентов (при α=0,05)

	Y1	X10	Х14	Х15	X16
Y1		-0,084348	0,572722	0,341947	-0,078507
X10	-0,084348		-0,037443	0,101525	-0,34006
Х14	0,572722	-0,037443		-0,160548	-0,100622
Х15	0,341947	0,101525	-0,160548		-0,161016
X16	-0,078507	-0,34006	-0,100622	-0,161016

 

14.Для значимых частных коэффициентов корреляции построим с заданной надёжностью γ интервальную оценку r_min< r < r_тах с помощью Z-преобразования Фишера (см. формулы в лекции). Получим следующий результат:

Таблица 9

Расчёт доверительных интервалов для частных генеральных коэффициентов корреляции иссле­дуемых экономических показателей с надёжностью γ = 0,95

	r	Z’	Zmin	Zmax	rmin	rтах
Y1X14	0,572722	0,651564	0,406564	0,896564	0,385551	0,714621
Y1X15	0,341947	0,356296	0,111296	0,601296	0,110838	0,537971
Х10Х16	-0,340055	-0,354155	-0,599155	-0,109155	-0,536448	-0,108723

 

15. Построим таблицу сравнения выборочных парных и частных коэффициентов корреляции для всех переменных.

Таблица 10

Таблица сравнения выборочных оценок парных и частных коэффициентов корреляции исследуе­мых показателей с выделением значимых коэффициентов (при α=0,05)

 

Между переменными	Коэффициент корреляции
парный	частный
Y1X10	-0,0215248	-0,084348
Y1X14	0,5772995	0,572722
Y1X15	0,3346368	0,341947
Y1X16	-0,2042044	-0,078507
Х10Х14	-0,03604	-0,037443
Х10Х15	0,153663	0,101525
Х10Х16	-0,34832	-0,34006
Х14Х15	0,077981	-0,160548
Х14Х16	-0,166761	-0,100622
Х15Х16	-0,25017	-0,161016

По полученным данным можно сделать следующие выводы:

1. Значимые корреляционные зависимости, полученные на этапе расчёта парных коэффициентов корреляции, подтвердились и при вычислении частных коэффициентов корреляции. При этом выявлены следующие механизмы воздействия переменных друг на друга: наиболее тесная связь наблюдается между изучаемым признаком Y₁ – производительность труда и факторными признаками Х₁₄ - фондовооруженность труда и Х₁₅ - оборачиваемость нормируемых оборотных средств (прямые зависимости) и между факторными признаками Х₁₀ – фондоотдача и X₁₆ - оборачиваемость ненормируемых оборотных средств(обратная зависимость).

2. Воздействие других переменных, что характерно для частного коэффициента корреляции (для парного коэффициента корреляции рассматриваются только две переменные без прочих посторонних), несколько ослабляет положительную взаимосвязь между производительностью труда (Y₁) и фондовооруженностью труда (Х₁₄), т.к. величина частного коэффициент корреляции r_y1x14/_x10x15x16 = 0,573 меньше величины парного коэффициента корреляции r_y1x14 = 0,577.

3. Аналогичная ситуация наблюдается и для обратной связи между фондоотдачей (Х₁₀) и
оборачиваемостью ненормируемых оборотных средств (X₁₆) - при исключении воздействия других
переменных абсолютная величина (взятая по модулю) парного коэффициент корреляции превышает абсолютное
значение частного коэффициента корреляции.

4. Для связи между производительностью труда (Y₁) и оборачиваемостью нормируемых оборотных средств (Х₁₅) характерна об­ратная ситуация: воздействие других переменных усиливает эту взаимосвязь (величина част­ного коэффициента корреляции больше величины парного коэффициента корреляции).

5. Наиболее сильная связь, выявленная на этапе расчёта парных коэффициентов корреляции,
между производительностью труда (Y₁) и фондовооруженностью труда (Х₁₄) остаёт­ся наиболее тесной и значимой и при расчете частных коэффициентов корреляции. Направление связи между данными показателями, как и в случаях с двумя другими значимыми коэффициентами, совпадает для парных и частных коэффициентов корреляции.

 

Расчёт множественных коэффициентов корреляции

 

Множественные коэффициенты корреляции служат мерой связи одной переменной с совме­стным действием всех остальных показателей.

16.Вычислим точечные оценки множественных коэффициентов корреляции. Множествен­ный коэффициент корреляции, например, для 1-го показателя Y₁ вычисляется по формуле:

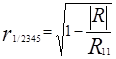
где | R | - определитель корреляционной матрицы R;

R_ij - алгебраическое дополнение элемента r_ij корреляцион­ной матрицы R.

Все алгебраические дополнения R_ij были найдены ранее, на этапе расчёта частных коэф­фициентов корреляции, поэтому осталось вычислить только определитель самой корреляцион­ной матрицы.

Чтобы найти определитель корреляционной матрицы, воспользуемся встроенной математи­ческой функцией Excel МОПРЕД. Получим |R|= 0,453494.

Подставляя полученное значение определителя в формулу, получаем значения множественных коэффициентов корреляции:

= 0,650726

= 0,376603

= 0,595674

= 0,422338

= 0,438828

 

 

Множественный коэффициент детерминации получается возведением коэффициента корре­ляции в квадрат.

17. Проверим значимость полученных множественных коэффициентов корреляции и детерми­нации. Проверка осуществляется с помощью F -критерия:

где k - количество рассматриваемых факторов (в нашем случае k = 5),

п - количество наблюдений.

Произведя расчёты, получим следующую таблицу:

Таблица 11

Множественные коэффициенты корреляции и детерминации исследуемых показателей с выде­лением значимых коэффициентов (на уровне значимости α = 0,05)

Множественный коэффициент корреляции	Множественный коэффициент детерминации r2	Значение стати­стики Fнабл
ry1/x10x14x15x16	0,650726	0,42344433	8,44603564
rx10/y1x14x15x16	0,376603	0,14182982	1,90060545
rx14/y1x10x15x16	0,595674	0,35482751	6,32469069
rx15/y1x10x14x16	0,422338	0,17836939	2,49655734
rx16/y1x10x14x15	0,438828	0,19257001	2,74272097

 

 

18. Для определения значимости множественных коэффициентов корреляции и детерминации нужно найти критическое значение F -распределения для заданного уровня значимости α и числа степеней свободы числителя v1=k-1 и знаменателя v2=n-k.

Для определения F_кр воспользуемся встроенной функцией Excel: ВСТАВКА - Функция - Статистические - FРАСПОБР, введя в диалоговое окно функции вероятность α = 0,05 и число степеней свободы v1=k-1=5-1=4 и v2=n-k=51-5-46.

Получаем F_кр = 2,574033

Если наблюдаемое значение F -статистики превосходит ее критическое значение, то гипотеза о равенстве нулю соответствующего множественного коэффициента корреляции отвергается.

Следовательно, в рассматриваемом примере значимыми являются множественные коэффициенты корреляции r_{y1/x10x14x15x16,} r_{x14/y1x10x15x16,} r_{x16/y1x10x14x15}. Множественные коэффициенты корреляции r_{x10/y1x14x15x16} и r_{x15/y1x10x14x16} являются незначимыми.

Результаты проведенного анализа позволяют сделать следующие выводы:

1.Множественный коэффициент корреляции r_{y1/x10x14x15x16} = 0,651 значим и имеет достаточно высокое значение, что говорит о том, показатель Y₁ – производительность труда имеет тесную связь с многомерным массивом факторных признаков Х₁₀ - фондоотдача, Х₁₄ - фондовооруженность труда, Х₁₅ - оборачиваемость нормируемых оборотных средств и X₁₆ - оборачиваемость ненормируемых оборотных средств. Это даёт ос­нование для проведения дальнейшего регрессионного анализа.

2.Множественный коэффициент детерминации r_{y1/x10x14x15x16}² = 0,423 показывает, что 42,3% доли дисперсии Y₁ – производительности труда, обусловлены изменениями факторных призна­ков.

3.Факторные признаки Х₁₄ - фондовооруженность труда и X₁₆ - оборачиваемость ненормируемых оборотных средств, также имеют значимые значения множественных коэффици­ентов корреляции и детерминации, что свидетельствует о их достаточно сильной взаимосвязи с рассматриваемыми признаками. Однако, хотя множественные коэффициенты фактора X₁₆ и значимы, но только 19,3% доли его дисперсии обусловлены изменениями переменных, включённых в рассматриваемую мо­дель, а, соответственно 80,7% его дисперсии обусловлены влиянием других, не включённых в модель факторов.

4.Полученные результаты корреляционного анализа, показавшие, что показатель Y₁ – производительность труда, имеет тесную связь с многомерным массивом факторных признаков, позволяют пе­рейти ко второму этапу статистического исследования - построению регрессионной модели.

 

Поделиться:

Воспользуйтесь поиском по сайту: