 |
Геометрическая вероятность
|
|
|
|
Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно.
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область.
Пусть эксперимент состоит в случайном выборе точки из некоторой области. Полагаем выбор любой точки равновозможным. Заданную в пространстве область обозначим W. В эксперименте, связанном со случайным выбором только одной точки из W, множество W является пространством элементарных событий. Случайными событиями в этом случае можно считать разные подмножества из W. Будем говорить, что случайное событие А наступило, если наугад выбранная точка x принадлежит подмножеству А, т.е.
Определение 18.2.4.
Пусть W – некоторый отрезок, L – его длина. А – отрезок длины l, принадлежащий W. Событие А состоит в попадании точки, брошенной в большой отрезок в А. Тогда
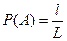
Аналогично, если множествомW элементарных исходов случайного эксперимента является фигура на плоскости площади S, а область А, ее подмножество, куда может попасть случайно брошенная на W точка, имеет площадь s, соответствующая вероятность события А – попадания в область А тогда
,
И, наконец, если речь идет об объемных фигурах, соответственно, W объема V и входящей в нее области А объема v
,
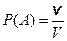Замечание 18.2.3.. Строго говоря, рассматриваемый здесь подход требует введения более общей характеристики (функции) множества – его меры (mes (A)), частными случаями которой являются длина, площадь и объем, и тогда вероятность события А будет отношением меры множества А к мере множества W
|
|
|
Пример 1. В квадрат вписан круг. Точка случайным образом бросается в квадрат. Какова вероятность того, что она попадет в круг? Согласно приведенной формуле соответствующая вероятность будет отношением площади круга к площади квадрата.
Пример 2. Два человека обедают в кафе в обеденный перерыв, который начинается у них в одно время и продолжается 1 час, от 12 до 13 часов. Каждый из них приходит в произвольный момент времени и обедает в течение 10 минут. Какова вероятность их встречи?
Пусть x — время прихода в кафе первого, а y — время прихода второго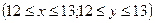 
. Встретиться они могут только тогда, когда оба находятся в кафе.
|
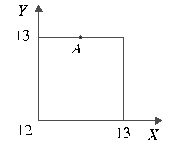
| Рис.1 |
Можно установить взаимно-однозначное соответствие между всеми парами чисел (x; y) (или множеством исходов) и множеством точек квадрата со стороной, равной 1, на координатной плоскости, где начало координат соответствует числу 12 по оси X и по оси Y, как изображено на рисунке 1. Здесь, например, точка А соответствует исходу, заключающемуся в том, что первый пришел в 12.30, а второй - в 13.00. В этом случае, очевидно, встреча не состоялась.
Если первый пришел не позже второго (y ³ x), то встреча произойдет при условии 0 £ y - x £ 1/6 (10 мин.- это 1/6 часа).
|
Если второй пришел не позже первого (x ³ y), то встреча произойдет при условии 0 £ x - y £ 1/6..
Таким образом, в первом случае нас будет удовлетворять условие y £ x + 1/6, а во втором
y ≥ x - 1/6. Область, удовлетворяющая этим двум условиям заштрихована на рис. 2
Рис. 2
Иными словами, в терминах геометрической вероятности, вероятность встречи есть отношение площади заштрихованной «полосы» между прямыми y = x + 1/6 и y = x - 1/6 внутри квадрата к площади самого квадрата.
Искомая вероятность p равна отношению площади заштрихованной области к площади всего квадрата.. Площадь квадрата равна единице, а площадь заштрихованной области можно определить как разность единицы и суммарной площади двух треугольников, изображенных на рисунке 7. Отсюда следует:
|
|
|
|
|
|
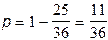
