 |
Общая характеристика работы
|
|
|
|
ТЕМПЕРАТУРНЫЕ ПОЛЯ, ИНИЦИИРОВАННЫЕ ХИМИЧЕСКИМИ РЕАКЦИЯМИ В ПОРИСТОЙ СРЕДЕ
01.04.14 – теплофизика и теоретическая теплотехника
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Стерлитамак
2006
Работа выполнена на кафедре теоретической физики Стерлитамакской государственной педагогической академии и в лаборатории физики и астрофизики Стерлитамакского филиала АН РБ
| Научный руководитель: | доктор технических наук, профессор Филиппов Александр Иванович |
| Научный консультант: | кандидат физико-математических наук, доцент Михайлов Павел Никонович |
| Официальные оппоненты: | доктор физико-математических наук, профессор Спивак Семен Израилевич кандидат физико-математических наук, доцент Ильясов Айдар Мартисович |
| Ведущая организация: | Уфимский государственный нефтяной технический университет |
Защита состоится «28» декабря 2006 г. в 10.00 часов на заседании диссертационного совета Д 212.013.04 при Башкирском государственном университете: 450074, г. Уфа, ул. Фрунзе, 32, ауд. 218.
С диссертацией можно ознакомиться в библиотеке Башкирского государственного университета
Автореферат разослан «28» ноября 2006 г.
 Ученый секретарь
Ученый секретарь
диссертационного совета,
д. ф.-м. н., профессор ____Р.Ф. Шарафутдинов
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность проблемы. Одной из наиболее актуальных проблем современной физики является разработка теории температурных полей, инициированных химическими реакциями в пористой среде. При этом возникают краевые задачи для нелинейных дифференциальных уравнений, отыскание решений которых представляет значительные трудности. Такие задачи широко распространены в химической кинетике. Особую значимость они приобретают в связи с различными технологическими приложениями. Например, в последнее время возрос интерес к кислотной обработке нефтяных пластов с карбонатосодержащим скелетом как к одному из способов повышения эффективности нефтедобычи. При кислотной обработке из-за разрушения скелета увеличивается проницаемость пористых сред, вследствие чего возрастает нефтеотдача. Для решения практических задач необходимо знать зависимость температуры и пористости от времени при различных концентрациях кислоты. Однако теория этих процессов до настоящего времени не создана.
|
|
|
Расчёт пространственно-временных распределений температуры и концентрации растворов химически реагирующих веществ в глубоко залегающих пластах сводится к решению краевых задач конвективной диффузии в пористых средах. Соответствующие задачи обладают большим разнообразием, и решение их зачастую сопряжено со значительными трудностями, которые обусловлены сложностью системы уравнений, описывающих взаимосвязанные процессы тепло- и массообмена с учетом химических реакций.
В настоящее время новые перспективы в исследовании динамики полей концентраций радиоактивных веществ открывает использование модификации асимптотических методов, созданной применительно к задачам скважинной термодинамики (А.И. Филиппов). Она была использована О.И. Коркешко (для создания теории температурных и массообменных процессов при закачке жидкости в пласты), Е.М Девяткиным, М.Р. Минлибаевым, Г.Я. Хусаиновой, П.Н. Михайловым, Г.Ф. Ефимовой, Н.П. Миколайчуком, О.В. Ахметовой (для исследования фильтрации газожидкостных смесей и аномальной жидкости, движения жидкости по скважине, термического воздействия на пласт на основе фильтрационно-волновых процессов).
|
|
|
С исследованием температурных полей в нефтегазовых пластах связано большое число работ научных школ Башкирского, Казанского, Латвийского госуниверситетов, научно-исследовательских и проектных институтов нефтегазовой промышленности, а также зарубежных исследователей. В подавляющем большинстве этих работах в основу исследований положена “схема сосредоточенной ёмкости”, которая предполагает, что поле температуры в интервале пласта не зависит от вертикальной координаты.
Все вышесказанное свидетельствует об актуальности выбранной проблемы исследования.
Целью диссертационной работы является построение модели физико-химического процесса взаимодействия соляной кислоты и карбонатной составляющей скелета и разработка методов расчётов полей температуры и плотности раствора кислоты в подземных горизонтах на основе применения метода асимптотического разложения к многослойным краевым задачам теплопроводности, описывающим взаимосвязанные поля температуры и концентрации кислоты при закачке жидкости в глубоко залегающие проницаемые пласты и изучение особенностей пространственно-временных распределений на этой основе.
Основные задачи исследования:
· анализ вклада основных физических процессов, обуславливающих динамику распространения раствора кислоты при воздействии на нефтегазовые пласты с целью увеличения нефтеотдачи, и постановка соответствующих математических задач; построение квазисолитонных решений для реакций первого и второго порядков и изучение зависимостей плотности кислоты от пористости и времени, пористости от времени и коэффициента химической реакции;
· применение метода асимптотического разложения к многослойным задачам о температурных полях, получение системы уравнений для коэффициентов разложения искомого решения в виде ряда по параметру разложения;
· получение аналитических решений для коэффициентов разложения нулевого и первого порядков;
· сопоставление полученных результатов с экспериментальными данными и результатами других исследователей;
· изучение особенностей формирования полей концентрации и температуры на основе результатов расчетов по разработанной теории и анализа экспериментальных данных.
|
|
|
Научная новизна. Получены новые аналитические решения задач, описывающих динамику и распространение раствора кислоты и температуры в проницаемых пластах. Установлены закономерности формирования температурных полей, обусловленных химическими реакциями. Построены квазисолитонные решения для реакций первого и второго порядков.
Достоверность полученных результатов обосновывается тем, что в основу исследований положены уравнения, выведенные из фундаментальных законов сохранения, согласованием полученных решений в частных случаях с результатами других исследователей, а также удовлетворительным согласием расчётных кривых с результатами экспериментальных исследований, опубликованными в печати.
Практическая ценность работы заключается в возможности использования результатов исследования в физике пористых сред, в нефтедобывающей промышленности. Полученные аналитические зависимости позволяют произвести оценку эффективности кислотной обработки и выбрать оптимальный режим. На основе полученных решений созданы новые методы расчётов полей температуры и концентрации кислоты в растворе, а изученные закономерности могут быть использованы для совершенствования способов исследования скважин и пластов.
Основные положения, выносимые на защиту:
1. Построенная с использованием модификации асимптотического метода математическая модель, описывающая взаимосвязанные поля температуры и концентрации раствора кислоты в жидкости, текущей по проницаемому пласту, окружённому непроницаемой средой, при воздействии на нефтяные и газовые карбонатосодержащие коллекторы нефти и газа.
2. Аналитические выражения для расчётов полей концентрации химически активных растворов веществ в естественных условиях при закачке в подземные пласты.
3. Результаты расчётов пространственно-временных распределений температуры, плотности раствора кислоты и пористости в естественных условиях, которые описывают особенности возникновения и формирования температурных аномалий в зонах реакции.
|
|
|
Апробация работы. Результаты работы докладывались и обсуждались на Международной конференции «Тихонов и современная математика», (г. Москва, 2006 г.), Международной научной конференции по математическому моделированию (г. Херсон, 2006 г.); V и VI Региональной школе-конференции для студентов, аспирантов и молодых ученых по математике и физике, БашГУ (г. Уфа, 2005 и 2006 гг.); IV Региональной научно-практической конференции «ЭВТ в обучении и моделировании», БГСПА (г. Бирск, 2005 г.); Всероссийской научной конференции «Современные проблемы физики и математики» (г. Стерлитамак 2004 г.); на научном семинаре кафедры математического анализа СГПА (научные руководители – д. ф.- м. н., проф. К.Б. Сабитов и д. ф.- м. н., проф. И.А. Калиев); объединенном научном семинаре кафедр геофизики и прикладной физики БашГУ (научные руководители – д. т. н., проф. Р.А. Валиуллин, д. т. н., проф. Л.А. Ковалева); научном семинаре кафедры теоретической физики СГПА (научный руководитель – д. т. н., проф. А.И. Филиппов).
Публикации. Основные результаты диссертации опубликованы в 8 научных работах, список которых приведен в конце автореферата. В работах [1] – [7] постановка задачи принадлежит профессору Филиппову А.И. В остальном вклад авторов равнозначный. Результаты, выносимые на защиту, принадлежат автору.
Структура и объём работы. Диссертация состоит из введения, трёх глав, заключения и списка литературы, состоящего из 235 наименований. Работа изложена на 149 страницах и иллюстрирована 21 рисунком.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность темы диссертационного исследования, сформулированы цель и задачи, обоснованы научная новизна и практическая ценность, приведены основные положения, выносимые на защиту.
Первая глава начинается с описания условий и геометрии задачи. Представлен обзор основных физических эффектов, имеющих место при кислотной обработке нефтегазовых пластов. Задача о температурном поле в скважинах при кислотном воздействии осложнена разнообразием практических условий. Произведён обзор основных физических процессов, происходящих при фильтрации жидкостей в глубокозалегающих пластах, дана оценка вкладов указанных физических процессов, и на этой основе осуществлена постановка задачи о фильтрации химически активной жидкости в глубоко залегающих пластах.
Выписаны уравнения, определяющие изменение температурного поля. После обезразмеривания произведена оценка вклада радиальной температуропроводности в процессы теплопереноса и делается вывод о возможности пренебрежения соответствующей составляющей в уравнении теплопереноса. Обоснована необходимость решения задачи, определяющей зависимость плотности кислоты от времени и координат.
|
|
|

|
| Рис. 1. Геометрия задачи. 1, 2 - непроницаемые области, I – зона движения кислоты, II – зона движения нефти |
Рассмотрена общая задача тепло- массопереноса (рис. 1), получающаяся в результате введения (вообще говоря, произвольного) параметра  , по которому проводится асимптотическое разложение, путем замены
, по которому проводится асимптотическое разложение, путем замены 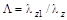 на
на  . В безразмерных координатах в предположении осевой симметрии параметризованная температурная задача имеет вид
. В безразмерных координатах в предположении осевой симметрии параметризованная температурная задача имеет вид
 , ,  , ,
| (1) |
 , ,  , ,
| (2) |

 , ,
| (3) |
 , ,  , ,
| (4) |
 , , 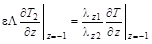 , ,
| (5) |
 , ,
| (6) |
 , , 
| (7) |

| (8) |
где  ,
, 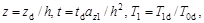
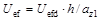 ,
, 
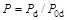 ,
,  ,
,  .
.
В качестве 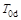 использовано максимальное повышение температуры. Функция плотности источников тепла q находится из решения химико-гидродинамической задачи. Нижний индекс «d» соответствует размерным величинам.
использовано максимальное повышение температуры. Функция плотности источников тепла q находится из решения химико-гидродинамической задачи. Нижний индекс «d» соответствует размерным величинам.
Искомые решения задачи представляются в виде усеченных асимптотических рядов по e

| (9) |
где нижние индексы относятся к номеру области, а верхние соответствуют порядковому номеру коэффициента разложения. При этом исходная задача является частным случаем более общей задачи при  =1.
=1.
После подстановки разложения по степеням параметра разложения ε в обезразмеренную систему уравнений и группировки коэффициентов при каждой степени параметра ε, получена бесконечная система уравнений, из которой следуют постановки задач для приближений требуемого порядка. Эти уравнения для пласта оказываются “зацепленными”, так как в них входят коэффициенты разложения соседних порядков  и
и  .
.
Процедура “расцепления” уравнений заключается в следующем. Из равенства нулю второй производной температуры в пласте для нулевого приближения по координате  , а также первых производных на границах
, а также первых производных на границах  , делается вывод, что в пределах пласта температура в нулевом приближении является функцией только двух переменных
, делается вывод, что в пределах пласта температура в нулевом приближении является функцией только двух переменных  и
и  и не зависит от
и не зависит от  . Слагаемые, содержащие нулевые и первые коэффициенты разложения в соответствующем уравнении, разбиваются на две группы. Все слагаемые, включающие температурное поле в нулевом приближении, не зависят от
. Слагаемые, содержащие нулевые и первые коэффициенты разложения в соответствующем уравнении, разбиваются на две группы. Все слагаемые, включающие температурное поле в нулевом приближении, не зависят от  и являются функциями только переменных
и являются функциями только переменных  и
и  . В результате по
. В результате по  получается обыкновенное дифференциальное уравнение второго порядка, которое легко интегрируется. Из соответствующих граничных условий построены соотношения, связывающие первые коэффициенты разложения в области
получается обыкновенное дифференциальное уравнение второго порядка, которое легко интегрируется. Из соответствующих граничных условий построены соотношения, связывающие первые коэффициенты разложения в области  (в пласте) с нулевыми приближениями в области
(в пласте) с нулевыми приближениями в области  (в окружающих породах). После подстановки полученных соотношений в исходное уравнение исключаются слагаемые первого порядка, которые заменяются граничными значениями производных в соседних областях. Это усложняет краевую задачу, но упрощает получение аналитических решений. Аналогичным образом производится “расцепление” последующих уравнений для коэффициентов более высокого порядка разложения.
(в окружающих породах). После подстановки полученных соотношений в исходное уравнение исключаются слагаемые первого порядка, которые заменяются граничными значениями производных в соседних областях. Это усложняет краевую задачу, но упрощает получение аналитических решений. Аналогичным образом производится “расцепление” последующих уравнений для коэффициентов более высокого порядка разложения.
В результате применения метода параметрического разложения получена бесконечная последовательность краевых задач для приближения соответствующего порядка. Осуществлена постановка задач теплопереноса для нулевого и первого коэффициентов разложения.
Установлено, что для получения решения задачи в первом приближении необходимо дополнительное интегральное условие, вывод которого также приводится в данной главе. Дополнительное интегральное условие получено на основе простых физических соображений и приводит к тривиальному решению осредненной задачи для остаточного члена усеченного асимптотического разложения.
Во второй главе осуществлена постановка задачи для общего случая, рассмотрены модели воздействия кислоты на скелет пористой среды, поставлены задачи, описывающие поля плотности раствора кислоты и пористости для реакций первого и второго порядков в цилиндрической и прямоугольной декартовой системах координат. Найдено аналитическое решение нелинейных задач химической кинетики, возникающих при кислотной обработке нефтяных пластов, и на этой основе построены функции плотности источников для продуктов химических реакций и градиента давления, входящие в уравнение энергии. Построены квазисолитонные решения для реакций первого и второго порядка в декартовых и цилиндрических координатах. Построены зависимости плотности кислоты от пористости среды, плотности кислоты от времени и коэффициента скорости реакции, пористости от времени и коэффициента скорости реакции, которые представляют аналитические выражения для расчётов полей концентрации химически активных растворов веществ в естественных условиях при закачке в подземные пласты.
Осуществлены расчеты пространственно-временных зависимостей плотности кислоты и пористости. Установлено, что размеры зоны активного кислотного воздействия в случае реакции первого порядка значительно превышают соответствующие размеры для реакции второго порядка. Показано, что размеры зоны реакции в пласте при больших временах неограниченно возрастают. Установлено, что значительные изменения пористости достигаются только многократными закачками кислоты.
Важной для практического использования является так называемая критическая пористость m = 0.910, которая соответствует случаю, когда однократная закачка соляной кислоты с максимальной плотностью ra0 = 212.5 кг/м3 полностью разъедает карбонатный пласт.
Третья глава посвящена решению задачи теплообмена в нулевом и первом приближениях. Для получения решений использован метод интегральных преобразований Лапласа–Карсона. Получено решение задачи теплообмена в нулевом приближении. Рассмотрены условия, позволяющие упростить задачу в нулевом и первом приближении, оценена погрешность асимптотического приближения.
Рассмотрены две группы задач, соответствующих практически важным случаям. Первая соответствует нахождению температурного поля в процессе закачки кислоты в пласт. Вторая описывает температурные поля после мгновенной закачки, когда основные процессы взаимодействия кислоты со скелетом происходят после прекращения движения раствора в пласте.
Найдены аналитические решения смешанных трехслойных краевых задач сопряжения со следами производных из внешних областей и дополнительным интегральным условием для нулевого и первого коэффициентов асимптотического разложения. Эти решения представляют формулы для расчетов температурных полей в пласте и окружающих породах в нулевом и первом приближениях. Показано, что в частном случае из нулевого приближения следуют известные решения, которые были построены ранее М.А.Пудовкиным, Л.И. Рубиншейном, Х.А. Ловерье и др. в предположениях «схемы сосредоточенной емкости». Поэтому полученное решение рассматриваемой задачи даже в нулевом приближении является более общим, чем все построенные ранее. Первое приближение, рассмотренное в следующем разделе, вообще ранее не было известно. Это доказывает, что построенные решения являются новыми.
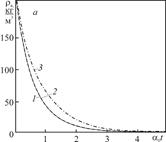
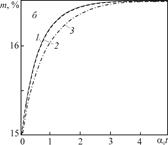
Проанализированы результаты расчётов пространственно-временных распределений концентраций кислоты и температурных полей в глубоко залегающих пористых пластах. На основе приведенных решений осуществлены расчеты химико-гидродинамических и температурных полей при различных коэффициентах реакции a(m). На рис. 2 показана зависимость плотности кислоты и пористости от безразмерного времени a0 t d (t d – размерное время). Расчеты проводились при следующих значениях параметров: rs = 2930 кг/м3, ra0 = 212.5 кг/м3, m 0 = 0.15, k = 0.73. Из рис. 2 видно, что с течением времени плотность закачиваемой кислоты падает, а пористость возрастает.
Для реакции первого порядка скорости изменения пористости при малых ее значениях и плотности кислоты минимальны для случая, когда коэффициент реакцииопределяется по формуле  , соответствующей случаю сферических полостей в начальном и в конечном
, соответствующей случаю сферических полостей в начальном и в конечном
| 
|
| Рис. 2. Зависимость плотности кислоты ra и пористости m от времени для реакции первого порядка: 1 – | |
состояниях (кривая 3); в то же время кривые 1 и 2 практически совпадают. Характерное безразмерное время процесса здесь составляет a0 t d ≈ 3. В остальных случаях характерное время реакции меньше; в частности, для реакции второго порядка оно составляет a0 t d ≈ 0.1. С учетом влияния ингибиторов соответствующие характерные времена возрастают. Из рис. 2 также следует, что изменение пористости при одном цикле закачки составляет приблизительно 2%; с увеличением начальной пористости соответствующие ее приращения возрастают.
Из вышеизложенного следует, что значительные изменения пористости достигаются только многократными закачками кислоты. На рис. 3 приведена зависимость конечной пористости от числа закачек. Например, при начальной пористости 10% необходимо 24 цикла закачки кислоты для полного разрушения карбонатного скелета.
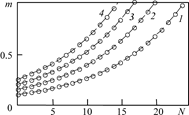
| Рис. 3. Зависимость пористости m от числа закачек N при различных ее начальных значениях m 0: 1 – m 0=0.1; 2 – 0.15; 3 – 0.2; 4 – 0.25 |
Важной для практического использования является так называемая критическая пористость m = 0.910, которая соответствует случаю, когда однократная закачка соляной кислоты с максимальной плотностью ra0 = 212.5 кг/м3 полностью разъедает карбонатный пласт. Это означает, что при меньших пористостях в результате однократной закачки кислоты скелет не может быть растворен полностью.
Для использования термических измерений при контроле кислотной обработки пластов важно знать величину максимальной температурной аномалии, обусловленной кислотным воздействием без учета теплообмена пласта с окружающими породами (рис. 4).
 
|
| Рис. 4 Зависимость максимальной величины термоаномалии D T однократного кислотного воздействия от начальной пористости m 0 – а и плотности закачиваемой кислоты ra0 – б: а) 1 – ra0 =212.5 кг/м3; 2 – 150; 3 – 100; 4 – 50; 5 – 20; б) 1 – m 0= 0.1; 2 – 0.2; 3 – 0.5; 4 – 0.91; 5 – 0.95; 6 – 0.98 |
Из рис. 4 а следует, что максимальная величина термоаномалии достигается при пористости m = 0.91 и плотности закачиваемой кислоты в растворе ra0 = 212.5 кг/м3 и соответствует D T = 53.9 K. Расчеты произведены при следующих значениях параметров: M = 0.1 кг/моль (СаСО3); rs=2930 кг/м3, c s = 1.67·106 Дж/(К×м3), с w = 4.19·106Дж/(К×м3), rw=1000 кг/м3, L = 830 кДж/кг. Зависимость величины термоаномалии от плотности закачиваемой кислоты – линейная (рис. 4, б). При начальной пористости выше критической m >0.91 на кривых имеются участки, когда с ростом плотности кислоты температура достигает максимального значения и при дальнейшем повышении плотности остается неизменной; физически это соответствует полному растворению скелета.
На рис. 5 представлены пространственно-временные зависимости температурной аномалии, обусловленной взаимодействием кислоты со скелетом, на оси скважины (r = 0). Расчеты произведены при l z 2 = l z 1, az 2 = az 1 в нулевом и первом приближениях. Предполагалось также, что радиальные размеры зоны реакции значительно превышают толщину пласта R >> h. В противном случае расчеты производились с учетом радиальной теплопроводности. На рис. 5, а изображена зависимость относительной температуры T от безразмерного времени t (числа Фурье Fo). Из рисунка следует, что процесс изменения температуры завершается при безразмерных временах t ≈ 2.
На рис. 5, б приведены зависимости относительной температуры T от безразмерной координаты z при различных безразмерных временах t в нулевом приближении, соответствующем усредненному по толщине пласта значению температуры. Кривые на рисунке позволяют определить размер зоны возмущения температуры, толщина которой приблизительно в два раза превышает толщину пласта. На рис. 5, в осуществлено сопоставление температурных кривых в первом (кривая 1) и нулевом (кривая 2) приближении при безразмерном времени t ≈ 0.3. Сравнение этих кривых показывает, что в нулевом приближении температура в интервале пласта не зависит от z; первое приближение уточняет распределение температуры, поскольку более детально описывает ее зависимость от координаты z в интервале пласта.
Для нулевого приближения в интервале пласта  температура постоянна, как и должно быть в соответствии со «схемой сосредоточенной ёмкости». Первый коэффициент разложения в пределах пласта принимает как отрицательные, так и положительные значения. Благодаря учету поправки, решение в первом приближении более реально отражает распределение температуры в пласте, что выражается в его зависимости от z. Из графиков видно, что в центральной части пласта нулевое приближение описывает распределение температуры с недостатком, а по краям – с избытком. В окружающих средах нулевое приближение всегда даёт избыточное значение температуры.
температура постоянна, как и должно быть в соответствии со «схемой сосредоточенной ёмкости». Первый коэффициент разложения в пределах пласта принимает как отрицательные, так и положительные значения. Благодаря учету поправки, решение в первом приближении более реально отражает распределение температуры в пласте, что выражается в его зависимости от z. Из графиков видно, что в центральной части пласта нулевое приближение описывает распределение температуры с недостатком, а по краям – с избытком. В окружающих средах нулевое приближение всегда даёт избыточное значение температуры.
  
|
| Рис. 5. Пространственно-временные распределения относительной температуры T: а) зависимость температуры в нулевом приближении в пласте от безразмерного времени t (числа Фурье); б) зависимость температуры в нулевом приближении от безразмерной координаты z при различных значениях безразмерного времени (1 – t = 0.1; 2 – 0.5; 3 – 1; 4 – 1.2; 5 – 1.6); в) сопоставление первого (кривая 1) и нулевого (кривая 2) приближений при t = 0.3 |
Из рис. 5 в следует также, что нулевое приближение описывает температурные поля в указанных условиях с точностью, достаточной в большинстве практических случаев.
Произведено сопоставление полученных результатов с теоретическими результатами других исследователей и с экспериментальными данными.
Отметим, что в условиях воздействия на пласты различными реагентами возникают аномалии температуры как в самом пласте, так и в зумпфе скважины. Возникновение аномалий в зумпфе происходит за счет заполнения реагентом, плотность которого, как правило, превышает плотность воды и сопутствующей конвекции замещения.
Термические исследования в скважине 838 Южно-Сургутской площади выполнены через 1 сут. после солянокислотной обработки: 3 – фоновый замер до начала работы компрессора; 4, 5 – замеры при закачке до прорыва газа; 5, 6, 7 – сразу, через 1 ч и через 2.5 ч после прорыва соответственно (рис. 6).
На фоновом замере отмечается значительная температурная аномалия в интервале перфорированных пластов (2 452–2 486 м). Зависимость температуры от глубины в указанном интервале, согласно представленной выше теории, обусловлена действием кислоты, поглощенной пластами, на карбонатную составляющую скелета.
В зумпфе скважины вблизи забоя регистрируется повышенный градиент температуры, свидетельствующий о нагревании забоя выпавшей вследствие конвекции замещения кислотой на забой скважины. По термозамерам при работе компрессора отмечается поток жидкости в оба перфорированных интервала. Из изложенного следует, что использование термометрии позволяет оценивать эффективность солянокислотной обработки призабойной зоны пласта.
 Рис. 6. Термические исследования после кислотной обработки в скважине 838 Южно-Сургутской площади. Обозначения: 1 – интервал перфорации; 2 – ПС; термограммы: 3 – фоновый замер; 4 – замер при продавке; 5 – сразу после прорыва воздуха; 6 – через 1 ч; 7 – через 2.5ч.
Рис. 6. Термические исследования после кислотной обработки в скважине 838 Южно-Сургутской площади. Обозначения: 1 – интервал перфорации; 2 – ПС; термограммы: 3 – фоновый замер; 4 – замер при продавке; 5 – сразу после прорыва воздуха; 6 – через 1 ч; 7 – через 2.5ч.
|
Итак, на основе асимптотического метода разработана теория, позволяющая рассчитывать температурные поля в нефтяных карбонатосодержащих пластах при кислотном воздействии. Это открывает новые перспективы для разработки способов контроля над процессом воздействия и совершенствования технологии кислотного воздействия.
В заключении подводятся итоги проведенного исследования.
|
|
|
12 |



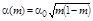 ; 2 –
; 2 –  ; 3 –
; 3 – 