Начало исследования циклов

Хотя циклы и были важной частью основных мировых культур и рели­гий на протяжении сотен лет, рассматривать их как двигатель эконо­мических колебаний стали лишь с начала XIX столетия. По иронии в памяти человечества первым человеком, искавшим в циклах способ понимания экономических изменений, остался не экономист, а астро­ном — сэр Уильям Гершель, открывший планету Уран. В 1801 г. Гер-шель заявил, что может существовать связь между циклами появления пятен на Солнце и погодой, что в свою очередь могло бы оказывать влияние на цену урожая и в итоге на экономику в целом. Примерно в то же время знаменитое семейство Ротшильдов в Европе, работая в обстановке строжайшей секретности, выделило в британских процент­ных ставках три цикла, включая 40-месячный.

В 1870-х годах идея периодичности экономических данных была выдвинута англичанином В. Стенли Джейвонсом и Сэмюэлем Бенне-ром, фермером из Огайо, которые сопоставили экономические данные своих стран с историческими данными о солнечных пятнах. В 1875 г. Беннер написал ныне знаменитый труд «Пророчества Беннера по по­воду будущего роста и падения цен». Он также утверждал, что его цик­лы находятся в зависимости от солнечной активности. Беннер опубли­ковал интересный график, предсказывающий экономические изменения вплоть до 1895 г. (рис. 16.3). Работавший примерно в то же время Кле­мент Джаглар обнаружил 10-12-годичные циклы в процентных ставках и экономике; теперь этот цикл носит его имя.

ГЛАВА 16. анализ циклов фьючерсных рынков 575

Рисунок 16.3. ЭКОНОМИЧЕСКИЕ ЦИКЛЫ, ПРЕДСКАЗАННЫЕ БЕННЕРОМ

Ротшильды тайно использовали свои циклы, до тех пор пока слухи не достигли в 1912 г. Нью-Йорка. Здесь группа инвесторов наняла математиков с целью обнаружения этих закономерностей. С момента воспроизведения формул Ротшильдов началось серьезное использова­ние циклов в инвестициях. В 1923 г. двое экономистов, профессора Крам и Китчин, обнаружили приблизительный 40-месячный цикл в эко­номических данных. Несмотря на то что Ротшильды открыли тот же самый цикл почти на век ранее, с 1923 г. он стал известен как цикл Китчина.

Реальный прогресс в изучении циклов начался с математических достижений в области анализа временных рядов и статистики в конце XIX-XX столетии. Некоторые из этих ключевых аналитических разра­боток — периодограмма, гармонический анализ и спектральный ана­лиз — обсуждаются в этой главе.

Интерес инвестирующей публики к циклам был сильно подогрет двумя анонимными версиями графиков Беннера, всплывшими в 30-е годы. По иронии об обеих этих версиях говорили, что они были найдены в старых столах офисов в штате Пенсильвании, одна — в Кон-неллсвилле, а другая — в Филадельфии. Коннеллсвилльский график стал известен под именем «перегонный» (distillery), поскольку был най­ден в столе, принадлежавшем компании «Overholt Distillery». Филадель­фийская версия графика была опубликована под названием «Предска­зание прошлого поколения» в «Уолл-стрит Джорнэл» 2 февраля 1933 г.

576 ЧАСТЬ 3. осцилляторы и циклы

Этот график моментально стал популярен, поскольку он якобы пред­сказывал Великую Депрессию. Версия графика Беннера, опубликован­ная «Уолл-стрит Джорнэл», тем не менее, очевидно была модифициро­вана таким образом, чтобы лучше соответствовать краху 1929 г., и по­казывала пик в 1929 г., а не в 1926 г., как это было на первоначаль­ном графике.

ОСНОВЫ ТЕОРИИ ЦИКЛОВ

Природа данных

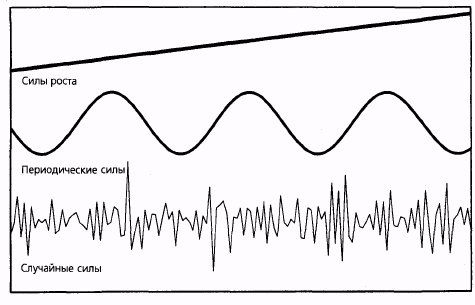
Любой ряд данных может быть разбит на три компонента: (1) силы ро­ста, (2) периодические силы и (3) случайные силы (рис. 16.4). Цикли­ческий анализ занимается поиском периодических или повторяющихся моделей в данных*.

Силы роста заставляют временные ряды медленно расти или снижать­ся с течением времени и фактически являются синонимом тенденции, или тренда. Случайные силы — это факторы, которые вызывают нере­гулярные колебания в данных, они по определению непредсказуемы. Циклический аналитик, обнаружив тренд, вычитает его из данных, что­бы удалить влияние сил роста, и сглаживает данные, чтобы удалить слу­чайные колебания, и, таким образом, находит периодические модели.

Циклическая модель

В начале XX века циклические аналитики стали пользоваться матема­тическим аппаратом для определения циклов. Цикл стали описывать как синусоидальную волну, используя при этом язык физики и статистики. С тех пор говорят, что у цикла есть частота, амплитуда и фаза, так же, как и у электромагнитных волн. Поскольку эта терминология универ­сально используется для описания циклов, важно ее определить.

* Слово «цикл» происходит от греческого слова, означающего круг, которое в своем наиболее общем смысле просто указывает на законченную последо­вательность событий, без подразумевания какой-либо регулярности во времен­ных интервалах. Циклический аналитик, тем не менее, озабочен периодичес­кими событиями, т. е. теми циклами, в которых наблюдается регулярность вре­менных интервалов.

ГЛАВА 16. анализ циклов фьючерсных рынков 577

Рисунок 16.4. ОСНОВНЫЕ КОМПОНЕНТЫ ДАННЫХ

Период и частота

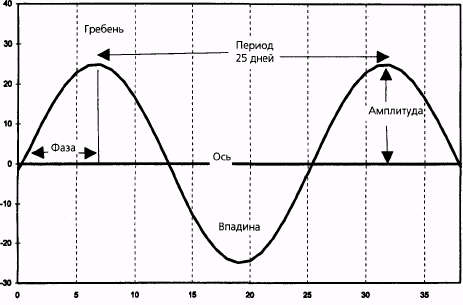
Длина цикла — временной отрезок от одного гребня до другого или от одной впадины до другой — называется его периодом (рис. 16.5). Частота — это количество циклов внутри определенного отрезка дан­ных, она обратно пропорциональна периоду:

частота = длина отрезка данных/период.

Например, для серии данных из 200 точек цикл с периодом 20 имел бы частоту 10 (10 = 200/20). Существует два основных математичес­ких метода анализа циклов — гармонический анализ и спектральный анализ. Первый из них основан,на периоде, а второй — на частоте.

Фаза, гребень и впадина

Фаза — это позиция определенной точки волны во времени. Гребень цикла — его самая высокая точка, а впадина — самая низкая точка (рис. 16.5). Фаза цикла обычно определяется положением гребня внут­ри цикла. Например, если длина цикла (период) равна 10 точкам дан-

578 ЧАСТЬ 3. осцилляторы и циклы

Рисунок 16.5. ИДЕАЛЬНАЯ МОДЕЛЬ ЦИКЛА

ных, а фаза равна 3, то первый гребень данных приходится на третью точку данных, с последующими гребнями, появляющимися в точках 13, 23, 33, 43, 53 и т.д.

Амплитуда и ось

Амплитуда — это сила колебаний, которая измеряется высотой греб­ня волны над ее осью (или глубиной впадины). Ось — это прямая ли­ния, вокруг которой колеблются данные в цикле. Амплитуда в цикли­ческом анализе измеряется от оси до гребня (рис. 16.5). Ось иногда называют точкой перегиба цикла.

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: