 |
Принцип проверки статистических гипотез
|
|
|
|
Генеральная совокупность и ее распределение.






Вариационный ряд. Относительная частота

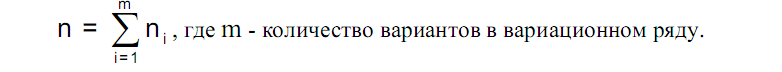
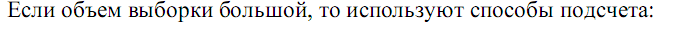

Статистический ряд. Полигон частот. Гистограмма
 Статистическое распределение записывается в виде таблицы: 1 строка – варианты; 2 строка – частоты.
Статистическое распределение записывается в виде таблицы: 1 строка – варианты; 2 строка – частоты.
n – объем выборки(частота).Иногда вместо частот используют относительную частоту:Wi = ni / n; ΣWi = 1 Разность между наибольшим и наименьшим элементами выборки называется размахом выборки, т.е. R = xmax-xmin
При большом объеме выборки ее элементы объединяются в группы. В процессе группированного ряда подсчитываются также накопленные частоты. ñi* - частота i-интервала равна сумме частот: ñ3* = ñ1+*ñ2*+ñ3*
Ŵi*- накопленная относительная частота.
Полигоном частот называется ломаная линия, вершинами которой служат точки с координатами (хi;ni), i=1…k.Для группировки выборки строят гистограмму частот, т.е. ступенчатую фигуру, состоящую из прямоугольников,площадь прямоугольника равна частоте ñi*.Площадь гистограммы равна объему выборки.
Высота прямоугольников равна ñ*i / n.
56.Числовые характеристики статистического распределения 




Распределение X-квадрат
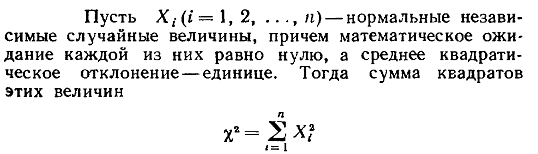

Распределение Стьюдента

Распределение Фишера

Метод моментов точечной оценки неизвестных параметров распределения.



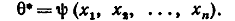


Метод наибольшего правдоподобия

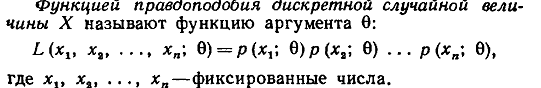

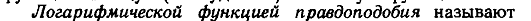
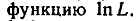

Интервальные оценки параметров.
2 подхода к рассм-ю инт. оценок:
-Байесовский
-Фон-Неймана(«Интерв. подходом»)
Пусть 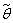 явл-ся точечн. оценкой неизв. параметра
явл-ся точечн. оценкой неизв. параметра 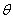 .
. 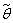 тем ближе к
тем ближе к 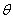 , чем меньше разность между ними:
, чем меньше разность между ними:

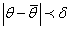 (1), тогда
(1), тогда  явл-ся точностью оценки. Эту точность невозможно опре-ть по соотнош-ю (1). Поступают след. образом:
явл-ся точностью оценки. Эту точность невозможно опре-ть по соотнош-ю (1). Поступают след. образом:  =0.95;0.975;0.99
=0.95;0.975;0.99
|
|
|
Она называется доверительной вероятностью или надежностью и потребуют вып-я (2)
(2) Р(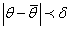 )=
)=  .
.
Т.к. выборка является случайной, то инт.оценка также явл-ся случайной, поэтому можно говорить о вероятности этой инт. оценки. границы дов. интервала также явл-ся СВ.
Общая схема постр-я довер. инт-ла:
1.Из генер. сов-ти с известн. законом распр-я F(x,  ) или f(x,
) или f(x,  ) СВ Х извл-ся выборка объема U, где
) СВ Х извл-ся выборка объема U, где 
неизв. параметр.
2. По выборке опред.точечн. оценку этого параметра.
3. строится ф-я К зависит от 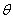 и оценки, назыв-ся статистикой и удовл-я след. св-вам: (К(
и оценки, назыв-ся статистикой и удовл-я след. св-вам: (К( ))
))
4.Задается доверит. вероят-ть  или Ур-нь знач-ти
или Ур-нь знач-ти 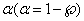
5.Исп-я закон распред-я стат. находят 2 значения К1 и К2, удовл. след. условию: Р(К1<К( )<К2)=
)<К2)= 
К1 и К2 находим из след. условий:
Р(К<К( )<К1)=
)<К1)=  ;
;
Р(К<К( )>К2)=
)>К2)=  ;
;
(К1,К2) наз-ся доверит.интервалом.
Метод наименьших квадратов.
Метод наименьших квадратов (МНК) - метод оценки параметров модели на основании экспериментальных данных, содержащих случайные ошибки. В основе метода лежат следующие рассуждения: при замене точного (неизвестного) параметра модели приблизительным значением необходимо минимизировать разницу между экспериментальными данными и теоретическими (вычисленными при помощи предложенной модели). Это позволяет рассчитать параметры модели с помощью МНК с минимальной погрешностью.
Мерой разницы в методе наименьших квадратов служит сумма квадратов отклонений действительных (экспериментальных) значений от теоретических. Выбираются такие значения параметров модели, при которых сумма квадратов разностей будет наименьшей – отсюда название метода:
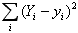 = min
= min
где Y – теоретическое значение измеряемой величины, y – экспериментальное.
При этом полученные с помощью МНК параметры модели являются наиболее вероятными.
Линейная регрессия.
Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.
|
|
|
В классической линейной регрессии предполагается, что наряду со стандартным условием  выполнены также следующие предположения (условия Гаусса-Маркова):
выполнены также следующие предположения (условия Гаусса-Маркова):
1) Гомоскедастичность (постоянная или одинаковая дисперсия) или отсутствие гетероскедастичности случайных ошибок модели: 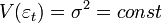
2) Отсутствие автокорреляции случайных ошибок: 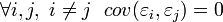
Данные предположения в матричном представлении модели формулируются в виде одного предположения о структуре ковариационной матрицы вектора случайных ошибок: 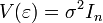
Кроме указанных предположений в классической модели факторы предполагаются детерминированными (нестохастическими). Кроме того, формально требуется, чтобы матрица  имела полный ранг (
имела полный ранг ( ), то есть предполагается, что отсутствует полная коллинеарность факторов.
), то есть предполагается, что отсутствует полная коллинеарность факторов.
При выполнении классических предположений обычный метод наименьших квадратов позволяет получить достаточно качественные оценки параметров модели, а именно, они являются несмещенными, состоятельными и наиболее эффективными оценками.
Принцип проверки статистических гипотез
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области - гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы - гипотезу принимают.
Поскольку критерий К - одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами, и, следовательно, существуют точки, которые их разделяют.
Критическими точками Ккр называют точки, отделяющие критическую область от области принятия гипотезы.
Различают, одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
Правосторонней называют критическую область, определяемую неравенством К>Ккр, где К кр - положительное число.
Левосторонней называют критическую область, определяемую неравенством К<Ккр, где К кр - отрицательное число.
|
|
|
Односторонней называют правостороннюю или левостороннюю критическую областью.
Двусторонней называют критическую область, определяемую неравенствами K<K1, K>K2, где К2>К1.
1. Правила суммы и произведения. Размещения, перестановки
2. Сочетания. Основные свойства чисел сочетаний
3. Пространство элементарных событий. Событие. Случайный эксперимент
4. Операции над случайными событиями
5. Свойства операций над случайными событиями
6. Классическое определение вероятности
7. Частота события. Статистическое определение вероятности
8. Геометрические вероятности
9. Алгебра событий, а-алгебра, вероятность, вероятностное пространство
10. Свойства вероятностей
11. Формула сложения вероятностей
12. Условная вероятность
13. Независимость событий
14. Формула полной вероятности
15. Формула Байеса
16. Схема независимых испытаний Бернулли
17. Наивероятнейшее число наступление события
18. Вероятность наступления события в интервале
19. Теорема Пуассона
20. Локальная теорема Муавра-Лапласа
21. Интегральная теорема Муавра-Лапласа
22. Дискретные случайные величины. Закон распределения дискретной случайной величины
23. Непрерывные случайные величины. Закон распределения непрерывной случайной величины
24. Функция распределения. Свойства функции распределения
25. Функция распределения дискретной случайной величины
26. Функция распределения непрерывной случайной величины
27. Плотность распределения непрерывной случайной величины. Свойства плотности распределения
28. Математическое ожидание, дисперсия и среднеквадратическое отклонение дискретной случайной величины
29. Математическое ожидание, дисперсия и среднеквадратическое отклонение непрерывной случайной величины
30. Свойства математического ожидания
31. Свойства дисперсии
32. Биномиальное распределение дискретной случайной величины
33. Распределение Пуассона дискретной случайной величины
34. Геометрическое распределение дискретной случайной величины
35. Равномерное распределение непрерывной случайной величины
|
|
|
36. Показательное распределение непрерывной случайной величины
37. Нормальное распределение непрерывной случайной величины
38. Правило «трёх сигм»
39. Системы случайных величин
40. Функция распределения системы случайных величин
41. Свойства двумерной функции распределения
42. Плотность распределения системы случайных величин. Свойства плотности распределения
43. Система двух случайных величин. Независимость. Условный закон распределения
44. Система двух случайных величин. Условная плотность непрерывных случайных величин. Теорема умножения плотностей распределения
45. Математическое ожидание и дисперсия системы дискретных случайных величин
46. Математическое ожидание и дисперсия системы непрерывных случайных величин
47. Корреляционный момент и коэффициент корреляции случайных величин
48. Свойства коэффициента корреляции
49. Функции одной дискретной случайной величины
50. Функции одной непрерывной случайной величины. Плотность распределения
51. Функции двух дискретных случайных величин
52. Функции двух непрерывных случайных величин. Формула свертки
53. Генеральная совокупность и ее распределение
54. Вариационный ряд. Относительная частота
55. Статистический ряд. Полигон частот. Гистограмма
56. Числовые характеристики статистического распределения
57. Распределении х-квадрат
58. Распределение Стьюдента
59. Распределение Фишера
60. Метод моментов точечной оценки неизвестных параметров распределения
61. Метод наибольшего правдоподобия
62.Интервальные оценки параметров
63.Метод наименьших квадратов
64.Линейная регрессия
65. Принцип проверки статистических гипотез
|
|
|


