Главная | Обратная связь | Поможем написать вашу работу!

Тестовые задания 2 рубежного контроля по дисциплине «биостатистика» для студентов 3 курса по специальностям «Медико-профилактическое дело» и «Сестринское дело»

~Статистические критерии делятся на:

|дискретные и непрерывные

|эмпирические и критические

|параметрические и непараметрические

|относительные и абсолютные

|простые и сложные

~Статистические критерии, предполагающие наличие нормального распределения переменных:

|непараметрические

|параметрические

|непрерывные

|прерывные

|нормальные

~Статистические критерии, использующие в процессе расчета характеристики распределения:

|непараметрические

|непрерывные

|прерывные

|параметрические

|нормальные

~Статистические критерии, использующие в процессе расчета ранги значений признака:

|параметрические

|непрерывные

|прерывные

|нормальные

|непараметрические

~К параметрическим критериям относится критерий:

|Пирсона

|Стьюдента

|Уилкоксона

|Колмогорова-Смирнова

|Манна-Уитни

~К параметрическим критериям относится критерий:

|Колмогорова-Смирнова

|Манна-Уитни

|Пирсона

|Фишера

|Уилкоксона

~Критерии Стьюдента и Фишера относятся к критериям:

|параметрическим

|непараметрическим

|непрерывным

|прерывным

|нормальным

~Критерии, применение которых не предполагает предварительного вычисления параметров распределения, называются:

|непараметрическими

|параметрическими

|непрерывными

|прерывными

|нормальными

~Порядковый номер значения признака называется:

|частотой

|рангом

|вариантом

|признаком

|уровнем

~Процедура упорядочения объектов исследования:

|соответствие

|классификация

|ранжирование

|систематизация

|выставление

~Аналогом двухвыборочного критерия Стьюдента является критерий:

|Уилкоксона

|Пирсона

|Манна-Уитни

|Фишера

|Колмогорова-Смирнова

~Аналогом парного критерия Стьюдента является критерий:

|Уилкоксона

|Манна-Уитни

|Пирсона

|Фишера

|Колмогорова-Смирнова

~Непараметрический критерий, используемый для сравнения двух независимых выборок:

|Уилкоксона

|Стьюдента

|Манна-Уитни

|Фишера

|Крускала-Уоллиса

~Непараметрический критерий, используемый для сравнения двух зависимых выборок:

|Манна-Уитни

|Стьюдента

|Фишера

|Уилкоксона

|Крускала-Уоллиса

~Критерий Уилкоксона применяется, если объемы выборок удовлетворяют условиям:

|2≤ n≤ 10

| n _1,2≥3 или n₁ =2, n₂ ≥5

|5≤ n≤ 50

| n _1,2≤30

| n _1,2≤3 или n₁ ≠2, n₂ ≥5

~Нулевая гипотеза «Н₀» для критерия Манна-Уитни имеет вид:

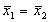
~Альтернативная гипотеза «Н₁» для критерия Манна-Уитни имеет вид:

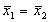
~Нулевая гипотеза «Н₀» для критерия Уилкоксона имеет вид:

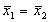
~Альтернативная гипотеза «Н₁» для критерия Уилкоксона имеет вид:

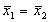
~Формула критерия Манна-Уитни:

~Расчетное значение критерия Уилкоксона определяется как... знаковых рангов.

|разность

|произведение

|сумма

|частное

|частное сумм

~Критерий Манна-Уитни рассчитывается с помощью:

|частот

|вариантов

|рангов

|дисперсии

|среднего

~ Критерий Уилкосона рассчитывается с помощью:

|частот

|вариантов

|рангов

|дисперсии

|среднего

~Дисперсионный анализ предложил ученый:

|Р. Фишер

|К. Пирсон

|Ф. Гальтон

|У. Госсет

|А. Кетле

~Статистический метод, используемый для выявления влияния отдельных факторов на изучаемый признак и оценку степени этого влияния, называется... анализом.

|регрессионным

|корреляционным

|кластерным

|дисперсионным

|дискриминантным

~При дисперсионном анализе проверяется нулевая гипотеза о:

|равенстве среднего некоторому значению

|равенстве дисперсий

|равенстве средних

|различии средних

|различии дисперсий

~Вид нулевой гипотезы «Н₀» при дисперсионном анализе:

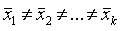
~Вид альтернативной гипотезы «Н₁» при дисперсионном анализе:

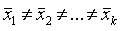
~Дисперсионный анализ может применяться, если для выборок выполнены условия:

|равномерно распределены, их дисперсии равны

|нормально распределены, их дисперсии неравны

|равномерно распределены, их дисперсии неравны

|нормально распределены, их дисперсии равны

|показательно распределены, их дисперсии равны

~Показатель, который оказывает влияние на конечный результат, называется:

|фактором

|аргументом

|откликом

|уровнем

|признаком

~Фактор - это:

|показатель, который оказывает влияние на конечный результат

|показатель, который не оказывает влияния на конечный результат

|значение измеряемого признака

|значение групповой средней

|показатель, который оказывает влияние на промежуточный результат

~Отклик на фактор - это:

|значение измеряемого признака

|показатель, который оказывает влияние на конечный результат

|показатель, который не оказывает влияния на конечный результат

|значение групповой средней

|показатель, который оказывает влияние на промежуточный результат

~Значение измеряемого признака в дисперсионном анализе называется:

|фактором

|откликом

|аргументом

|уровнем

|признаком

~При дисперсионном анализе если фактор оказывает воздействие на величину отклика, то нулевая гипотеза о равенстве средних:

|отвергается

|принимается

|игнорируется

|формулируется заново

|не рассматривается

~При дисперсионном анализе если фактор не оказывает воздействия на величину отклика, то нулевая гипотеза о равенстве средних:

|отвергается

|игнорируется

|формулируется заново

|не рассматривается

|принимается

~В зависимости от количества изучаемых действий на явления дисперсионный анализ делится на:

|простой и сложный

|одинарный и множественный

|однофакторный и многофакторный

|дискретный и непрерывный

|парный и двухвыборочный

~Выборочные данные для однофакторного дисперсионного анализа оформляют в виде:

|диаграммы

|рисунка

|таблицы

|формулы

|схемы

~При дисперсионном анализе общая дисперсия разбивается на:

|простую и сложную

|дискретную и непрерывную

|факторную и остаточную

|абсолютную и относительную

|постоянную и переменную

~Формула факторной дисперсии:

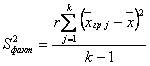
~Формула остаточной дисперсии:

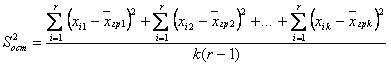
~ Формула общей дисперсии:

~Дисперсия, которая соответствует влиянию фактора на изменение средних значений выборки, называется:

|остаточной

|общей

|факторной

|средней

|простой

~Дисперсия, возникающая по случайными причинами и не влияющая на изменение средних значений выборки, называется:

|остаточной

|факторной

|общей

|средней

|простой

~Сумма факторной и остаточной дисперсий называется:

|частичной

|положительной

|отрицательной

|общей

|выборчной

~При дисперсионном анализе используется критерий:

|Стьюдента

|Пирсона

|Фишера

|Колмогорова-Смирнова

|Манна-Уитни

~Критерий F_расч, используемый при дисперсионном анализе, определяется по формуле:

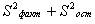
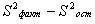
~Аналогом однофакторного дисперсионного анализа является критерий:

|Крускала-Уоллиса

|Манна-Уитни

|Пирсона

|Фишера

|Колмогорова-Смирнова

~Непараметрический критерий, используемый для сравнения трех и более независимых групп:

|Крускала-Уоллиса

|Манна-Уитни

|Пирсона

|Фишера

|Колмогорова-Смирнова

~Критерий Крускала-Уоллиса рассчитывается с помощью:

|частот

|рангов

|вариантов

|дисперсии

|среднего

~Критерий Крускала-Уоллиса асимптотически приближается к распределению:

| t -Стьюдента

| F -Фишера

| χ² -Пирсона

| Ф -Лапласа

| W -Уилкоксона

~ При критерии Крускала-Уоллиса проверяется нулевая гипотеза о:

|равенстве среднего некоторому значению

|равенстве дисперсий

|равенстве средних

|различии средних

|различии дисперсий

Вид нулевой гипотезы «Н₀» критерия Крускала-Уоллиса:

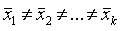
~ Вид альтернативной гипотезы «Н₁» критерия Крускала-Уоллиса имеет вид:

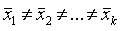
~Формула критерия Крускала-Уоллиса:

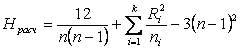
~При двухфакторном дисперсионном анализе формулируется … пары гипотез.

~Для количественной оценки факторов риска развития заболевания используется … анализ.

|регрессионный

|дискриминантный

|кластерный

|корреляционный

|дисперсионный

~Термин «корреляция» ввел:

|Ф. Гальтон

|К. Пирсон

|Р. Фишер

|Ж. Кювье

|Ч. Дарвин

~В статистике термин «корреляция» первым стал использовать:

|Ж. Кювье

|К. Пирсон

|Ф. Гальтон

|Р. Фишер

|Ч. Дарвин

~Количественный метод определения тесноты и направления связи между двумя и более случайными величинами - это... анализ.

|регрессионный

|дискриминантный

|кластерный

|дисперсионный

|корреляционный

~Показатель, характеризующий силу связи и ее направление:

|коэффициент детерминации

|ошибка аппроксимации

|коэффициент вариации

|коэффициент корреляции

|размах вариации

~Коэффициент корреляции характеризует:

|силу и направление связи между признаками

|степень разброса случайной величины от ее среднего значения

|разность между максимальным и минимальным значениями признака

|среднее отклонение расчетных значений от фактических

|среднее значение случайной величины

~ Для оценки силы связи в теории корреляции применяется шкала:

|Чеддока

|Спирмена

|Пирсона

|Фишера

|Стьюдента

~Линейный коэффициент корреляции принимает значения в промежутке:

|[-1, 1]

|[0, 1]

|[-1, 0]

|[0, 10]

|[-10, 0]

~По направлению корреляционную связь различают:

|прямую и обратную

|сильную и слабую

|первичную и вторичную

|абсолютную и относительную

|зависимую и независимую

~Корреляционная связь, при которой увеличение среднего значения одной переменной влечет увеличение среднего значения другой переменной:

|обратная

|сильная

|прямая

|слабая

|умеренная

~ Корреляционная связь, при которой увеличение среднего значения одной переменной влечет уменьшение среднего значения другой переменной:

|прямая

|сильная

|обратная

|слабая

|умеренная

~При прямой связи коэффициент корреляции принимает значения:

|от -1 до 0

|от -1 до 1

|от -10 до 10

|от 0 до 1

|от 0 до 10

~При обратной связи коэффициент корреляции принимает значения:

|от 0 до 1

|от -1 до 1

|от -10 до 10

|от -1 до 0

|от 0 до 10

~Если коэффициент корреляции равен 0, то связь между явлениями:

|присутствует

|частичная

|отсутствует

|функциональная

|обратная

~Если коэффициент корреляции равен «+1» или «–1», то связь между явлениями:

|функциональная

|отсутствует

|присутствует

|частичная

|обратная

~Если 0,1< r_xy <0,3, то связь:

|слабая

|умеренная

|сильная

|отсутствует

|обратная

~Если 0,3< r_xy <0,5, то связь:

|умеренная

|сильная

|отсутствует

|обратная

|слабая

~Если 0,5< r_xy <0,7, то связь:

|умеренная

|отсутствует

|обратная

|слабая

|заметная

~Если 0,7< r_xy <0,9, то связь:

|высокая

|умеренная

|заметная

|обратная

|слабая

~Если 0,9< r_xy <1, то связь:

|умеренная

|заметная

|сильная

|обратная

|высокая

~Связь между признаками слабая, если:

|0,3 < r_xy < 0,5

|0,5 < r_xy < 0,7

|0,1 < r_xy < 0,3

|0,7 < r_xy < 0,9

|0,9< r_xy < 1

~Связь между признаками умеренная, если:

|0,3 < r_xy < 0,5

|0,1 < r_xy < 0,3

|0,5 < r_xy < 0,7

|0,7 < r_xy < 0,9

|0,9< r_xy < 1

~Связь между признаками заметная, если:

|0,5 < r_xy < 0,7

|0,3 < r_xy < 0,5

|0,1 < r_xy < 0,3

|0,7 < r_xy < 0,9

|0,9< r_xy < 1

~Связь между признаками высокая, если:

|0,7 < r_xy < 0,9

|0,5 < r_xy < 0,7

|0,3 < r_xy < 0,5

|0,1 < r_xy < 0,3

|0,9< r_xy < 1

~Связь между признаками сильная, если:

|0,7 < r_xy < 0,9

|0,5 < r_xy < 0,7

|0,9< r_xy < 1

|0,3 < r_xy < 0,5

|0,1 < r_xy < 0,3

~При анализе зависимости между двумя переменными применяют:

|гистограммы

|полигоны

|диаграммы рассеяния

|радиальные диаграммы

|столбиковые диаграммы

~Диаграмма рассеяния, представленная на рисунке, характеризует … связь.

|обратную

|функциональную

|качественную

|прямую

|нормальную

~Диаграмма рассеяния, представленная на рисунке, характеризует … связь.

|прямую

|функциональную

|качественную

|нормальную

|обратную

~ Диаграмма рассеяния, представленная на рисунке, характеризует:

|прямую связь

|обратную связь

|функциональную связь

|отсутствие связи

|наличие связи

~Линейный коэффициент корреляции:

~ :

|коэффициент регрессии

|коэффициент детерминации

|средняя ошибка аппроксимации

|линейный коэффициент корреляции

|коэффициент вариации

~Парный коэффициент корреляции является:

|непараметрическим

|относительным

|абсолютным

|параметрическим

|базисным

~Средняя ошибка коэффициента корреляции:

~ :

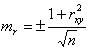
|линейный коэффициент корреляции

|коэффициент детерминации

|средняя ошибка аппроксимации

|средняя ошибка коэффициента корреляции

|коэффициент вариации

~Коэффициент корреляции достоверный, если не менее чем в … раз(-а) превышает свою среднюю ошибку.

~Между стажем работы ткачих и частотой понижения слуха у них установлена корреляционная зависимость, r_xy = 0,8. Сила и направление связи:

|высокая, прямая

|слабая, обратная

|умеренная, прямая

|сильная, обратная

|слабая, прямая

~Между частотой материнской смертности и частотой внебольничного аборта установлена корреляционная зависимость, r_xy = 0,69. Сила и направление связи:

|умеренная, прямая

|слабая, обратная

|заметная, прямая

|сильная, обратная

|высокая, прямая

~Между частотой заболеваемости кариесом детей и содержанием фтора в питьевой воде установлена корреляционная зависимость, r_xy = -0,85. Сила и направление связи:

|умеренная, прямая

|сильная, прямая

|слабая, обратная

|высокая, обратная

|заметная, прямая

~Между частотой заболеваемости инфарктом миокарда и среднемесячной температурой воздуха установлена корреляционная зависимость, r_xy = -0,75. Сила и направление связи:

|умеренная, прямая

|сильная, прямая

|заметная, обратная

|высокая, обратная

|слабая, прямая

~К непараметрическим коэффициентам связи нельзя отнести:

|коэффициент ранговой корреляции Спирмена

|коэффициент контингенции Пирсона

|линейный коэффициент корреляции Пирсона

|коэффициент сопряженности Чупрова

|коэффициент ассоциации Юла

~Коэффициент ранговой корреляции предложен:

|Ф. Гальтоном

|К. Пирсоном

|А. Кетле

|Ч. Дарвиным

|Ч. Спирменом

~Коэффициент ранговой корреляции Спирмена:

~ :

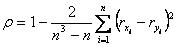
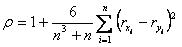
|линейный коэффициент корреляции Пирсона

|коэффициент контингенции Пирсона

|коэффициент сопряженности Чупрова

|коэффициент ранговой корреляции Спирмена

|коэффициент ассоциации Юла

~Коэффициент ранговой корреляции Спирмена принимает значения в промежутке:

|[0; 1]

|[-1; 0]

|[-1; 1]

|[-10; 10]

|[1; 10]

~Коэффициент ранговой корреляции Спирмена используется для определения тесноты связей как между …, так и между … признаками.

|относительными, абсолютными

|простыми, сложными

|базовыми, цепными

|количественными, качественными

|экстенсивными, интенсивными

~Коэффициент ранговой корреляции Спирмена применяется, если объемы выборок удовлетворяют условию:

|1≤ n _1,2≤50

|5≤ n _1,2≤40

|5≤ n _1,2≤30

|4≤ n _1,2≤40

|3≤ n _1,2≤40

~Термин «регрессия» ввел:

|Ф. Гальтон

|Р. Фишер

|К. Пирсон

|А. Кетле

|В. Уэлдон

~Метод статистической обработки данных, позволяющий измерить связь между одной или несколькими причинами и следствием - это … анализ.

|регрессионный

|дисперсионный

|дискриминантный

|корреляционный

|статистический

~По количеству признаков различают регрессию:

|простую, сложную

|парную, множественную

|слабую, сильную

|прямую, обратную

|постоянную, переменную

~По направлению связи различают регрессию:

|парную, множественную

|простую, сложную

|прямую, обратную

|слабую, сильную

|постоянную, переменную

~Если результативный признак рассматривается как функция от одного аргумента, то регрессия:

|одинарная

|парная

|множественная

|простая

|линейная

~Если результативный признак рассматривается как функция от нескольких аргументов, то регрессия:

|парная

|одинарная

|множественная

|простая

|линейная

~Общий вид уравнения парной регрессии:

|y=f(x₁, x₂,…, x_n)

| y=f(x)

|y=ax+b

| y=a+b/x

| y= ax^b

~Общий вид уравнения множественной регрессии:

|y=f(x₁, x₂,…, x_n)

|y=ax+b

| y=a+b/x

| y= ax^b

| y=f(x)

~Линейное уравнение парной регрессии:

| y=e^ax+b

| y=a+b/x

| y=a+b₁x+b₂x²

| у=a+bx

| y=ab^x

~Экспоненциальное уравнение парной регрессии:

| у=a+bx

| y=a+b/x

| y=e^ax+b

| y=a+b₁x+b₂x²

| y=ab^x

~Гиперболическое уравнение парной регрессии:

| y=a+b/x

| y=e^ax+b

| у=a+bx

| y=a+b₁x+b₂x²

| y=ab^x

~Параболическое уравнение парной регрессии:

| y=a+b/x

| y=e^ax+b

| у=a+bx

| y=a+b₁x+b₂x²

| y=ab^x

~Показательное уравнение парной регрессии:

| y=a+b₁x+b₂x²

| y=ab^x

| y=a+b/x

| y=e^ax+b

| у=a+bx

~ у=a+bx - … уравнение парной регрессии.

|экспоненциальное

|линейное

|гиперболическое

|параболическое

|показательное

~ y=a+b₁x+b₂x² - … уравнение парной регрессии.

|линейное

|экспоненциальное

|гиперболическое

|показательное

|параболическое

~ y=a+b/x - … уравнение парной регрессии.

|показательное

|гиперболическое

|параболическое

|линейное

|экспоненциальное

~ y=e^ax⁺^b - … уравнение парной регрессии.

|параболическое

|линейное

|экспоненциальное

|гиперболическое

|показательное

~ y=ab^x - … уравнение парной регрессии.

|экспоненциальное

|гиперболическое

|параболическое

|линейное

|показательное

~Построение уравнения регрессии сводится к оценке:

|независимой переменной

|коэффициентов

|результативного признака

|факторного признака

|зависимой переменной

~Коэффициенты уравнения регрессии определяются с помощью метода:

|наименьших квадратов

|доверительных интервалов

|корреляционного анализа

|статистического наблюдения

|дисперсионного анализа

~Суть метода наименьших квадратов:

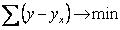
~Формула определения свободного коэффициента линейного уравнения парной регрессии:

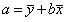
~Формулы определения коэффициентов линейного уравнения парной регрессии:

~Для оценки статистической значимости коэффициентов регрессии используется критерий:

|Фишера

|Пирсона

|Стьюдента

|Манна-Уитни

|Колмогорова-Смирнова

~Нулевая гипотеза критерия Стьюдента при проверке значимости коэффициентов регрессии имеет вид:

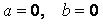
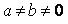
~Альтернативная гипотеза критерия Стьюдента при проверке значимости коэффициентов регрессии имеет вид:

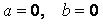
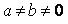
~Проверка значимости уравнения регрессии проводится с помощью критерия:

|Фишера

|Пирсона

|Стьюдента

|Манна-Уитни

|Колмогорова-Смирнова

~При проверке значимости уравнения регрессии определяется:

~Коэффициент детерминации принимает значения в промежутке:

|[-1; 1]

|[-1; 0]

|[0; 1]

|[-10; 10]

|[1; 10]

~Коэффициент … показывает, какая доля признака «у» учтена в анализе и вызвана влиянием на нее факторов, включенных в анализ.

|детерминации

|корреляции

|вариации

|ассоциации

|контингенции

~Уравнение регрессии является качественным, если коэффициент детерминации:

| ≤0,8

| ≥0

| ≤0

| ≥0,8

|=0

~Совокупность значений какого-либо показателя за несколько последовательных моментов или периодов называется:

|законом распределения

|функцией распределения

|выборкой

|динамическим рядом

|вариационным рядом

~… ряд характеризует изменение размеров явления на определенную дату.

|Моментный

|Интервальный

|Гармонический

|Вариационный

|Динамический

~… ряд характеризует изменения размеров явления за определенный период.

|Моментный

|Гармонический

|Интервальный

|Вариационный

|Динамический

~Функция от времени, определяющая основную тенденцию развития показателя во времени:

|тренд

|вариант

|ряд

|экспонента

|дисперсия

~К способам выравнивания динамического ряда не относится:

|укрупнение периодов

|расчет групповой средней

|интервальная оценка

|расчет скользящей средней

|метод наименьших квадратов

~Временной ряд состоит из … элементов.

~Уравнение линейного тренда:

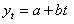
~ Формула свободного коэффициента уравнения линейного тренда:

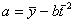
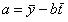
~Формула коэффициентов уравнения линейного тренда:

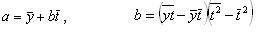
~… показатели характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базовый уровень, до данного (i -го) периода.

|Цепные

|Абсолютные

|Базисные

|Относительные

|Средние

~… показатели характеризуют интенсивность изменения уровня от периода к периоду в пределах изучаемого промежутка времени.

|Базисные

|Абсолютные

|Цепные

|Относительные

|Средние

~Показатель динамики, определяемый как разность между двумя уровнями динамического ряда:

|абсолютный прирост

|темп роста

|темп прироста

|коэффициент роста

|коэффициент опережения

~Показатель динамики, определяемый как отношение двух сравниваемых уровней динамического ряда:

|темп роста

|коэффициент роста

|абсолютный прирост

|темп прироста

|коэффициент опережения

~Показатель динамики, характеризующий скорость изменения признака в единицу времени, выраженную в процентах:

|коэффициент роста

|абсолютный прирост

|темп роста

|темп прироста

|коэффициент опережения

~Показатель динамики, показывающий на сколько процентов уровень данного периода больше (или меньше) базисного уровня:

|коэффициент роста

|темп роста

|темп прироста

|абсолютный прирост

|коэффициент опережения

~Показатель динамики, рассчитываемый в процентах как отношение абсолютного прироста к темпу прироста за тот же период времени:

|значение коэффициента 10% роста

|темп прироста

|абсолютное значение 1% прироста

|абсолютный прирост

|коэффициент опережения

~Показатель динамики, рассчитываемый как отношение темпов роста за одинаковые отрезки времени по двум динамическим рядам:

|абсолютное значение 1% прироста

|коэффициент опережения

|значение коэффициента 10% роста

|темп прироста

|абсолютный прирост

~Средняя величина изменения показателя за интервал времени:

|абсолютное значение 1% прироста

|средний коэффициент роста

|темп прироста

|средний абсолютный прирост

|абсолютный прирост

~Абсолютный базисный прирост:

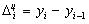
~Абсолютный цепной прирост:

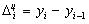
~Базисный коэффициент роста:

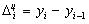
~Цепной коэффициент роста:

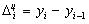
~Абсолютное значение 1% прироста:

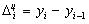
~Темп роста:

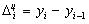
~Базисный темп прироста:

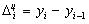
~Цепной темп прироста:

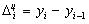
~Коэффициент опережения:

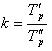
~Средний абсолютный прирост:

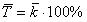
~Средний темп роста:

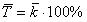
~Средний темп прироста:

~Метод … применяется при сравнении интенсивных показателей в совокупностях, отличающихся по составу.

|дисперсионного анализа

|стандартизации

|выборочного исследования

|корреляционного анализа

|вариации

~Метод … позволяет устранить возможное влияние различий в составе совокупностей по каком

Воспользуйтесь поиском по сайту: