Оценка случайных погрешностей.

Понятие физической величины и единицы ее измерения.

Физи́ческая величина́ — свойство материального объекта или явления, общее в качественном отношении для класса объектов или явлений, но в количественном отношении индивидуальное для каждого из них[1]. Физические величины имеют род, размер, единицу(измерения) и значение.

Единица измерения физической величины (англ. unit of measurement) – физическая величина фиксированного размера, которой условно присвоено числовое значение, равное 1, и применяемая для количественного выражения однородных с ней физических величин. Примечание. На практике широко применяется понятие узаконенные единицы, которое раскрывается как «система единиц и (или) отдельные единицы, установленные для применения в стране в соответствии с законодательными актами».

Международная система СИ.

Согласованная Международная система единиц физических величин была принята в 1960 г. XI Генеральной конференцией по мерам весам. Международная система - СИ (SI), SI - начальные буквы французского наименования Systeme International. В системе предусмотрен перечень из семи основных единиц: метр, килограмм, секунда, ампер, кельвин, кандела, моль и двух дополнительных: радиан, стерадиан, а также даны приставки для образования кратных и дольных единиц.

Понятия об измерении.

Измерение — совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).

 

Прямые и косвенные измерения.

Прямые измерения - это такие измерения, при которых искомое значение физической величины определяется непосредственно путём сравнения с мерой этой величины.

Косвенное измерение — измерение, при котором искомое значение величины находится на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Мерное параллельно или вблизи мерного. Вот...

• сопротивление резистора находим на основании закона Ома подстановкой значений силы тока и напряжения, получаемых в результате прямых измерений. (Проводим прямое измерение напряжения, проводим прямое измерение тока, потом на основании полученных ДВУХ чисел получаем косвенное «измерение» сопротивления)

Методы прямых измерений.

Метод измерения - совокупность приемов использования принципов и средств измерений. Измерения производятся одним из двух методов: методом непосредственной оценкиили методом сравнения с мерой.

Метод непосредственной оценки - метод, при котором значение искомой величины определяют непосредственно по отсчетному устройству измерительного прибора. Пример методанепосредственной оценки - измерение тока амперметром.

Метод сравнения с мерой - метод измерения, при котором измеряемую искомую величину сравнивают с однородной величиной, воспроизводимой мерой. Метод сравнения с мерой имеет ряд разновидностей:

- дифференциальный метод,

- нулевой метод,

- метод замещения и др.

 

При дифференциальном методе на измерительный прибор воздействует разность между измеряемой и образцовой величинами, воспроизводимой мерой. Чем меньше разность, тем точнее результат.

Предельным случаем дифференциального метода является нулевой метод, при котором разность доводится до нуля.

При использовании метода замещения, измеряемая величина замещается известной величиной, воспроизводимой мерой. При этом замещение измеряемой величины производят так, что никаких измерений в схеме не происходит, то есть показания прибора будут одинаковы в обоих случаях

Виды погрешностей.

Выделяют следующие виды погрешностей:

1. абсолютная погрешность;
2. относительна погрешность;
3. приведенная погрешность;
4. основная погрешность;
5. дополнительная погрешность;
6. систематическая погрешность;
7. случайная погрешность;
8. инструментальная погрешность;
9. методическая погрешность;
10. субъективная погрешность;
11. статическая погрешность;
12. динамическая погрешность.

Абсолютная погрешность - это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.

Относительная погрешность - это число, отражающее степень точности измерения.

Приведенная погрешность - это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.

Основная погрешность - это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).

Дополнительная погрешность - это погрешность, которая возникает в условиях несоответствия значений влияющих величин их нормальным значениям, или если влияющая величина переходит границы области нормальных значений.

Систематическая погрешность - это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины. Обычно систематическую погрешность пытаются исключить возможными способами (например, применением методов измерения, снижающих вероятность ее возникновения), если же систематическую погрешность невозможно исключить, то ее просчитывают до начала измерений и в результат измерения вносятся соответствующие поправки. В процессе нормирования систематической погрешности определяются границы ее допустимых значений. Систематическая погрешность определяет правильность измерений средств измерения (метрологическое свойство).

Случайной погрешностью измерения называется погрешность, которая при многократном измерении одного и того же значения не остается постоянной. Например, при измерении валика одним и тем же прибором в одном и том же сечении получаются различные значения измеренной величины.

Инструментальная погрешность - это погрешность, возникающая из-за допущенных в процессе изготовления функциональных частей средств измерения ошибок.

Методическая погрешность - это погрешность, возникающая по следующим причинам:

1) неточность построения модели физического процесса, на котором базируется средство измерения;

2) неверное применение средств измерений.

 

Субъективная погрешность - это погрешность возникающая из-за низкой степени квалификации оператора средства измерений, а также из-за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.

Статическая погрешность - это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.

 

Динамическая погрешность - это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).

 

Оценка случайных погрешностей.

 

Использование функций распределения.

Присутствие случайных погрешностей в результатах измере­ний легко обнаруживается из-за их разброса относительно некото­рого значения. C известными оговорками, результат измерения и его погрешность могут рассматривать­ся как случайные величины.

Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их ин­тегральных или дифференциальных функций распределения.

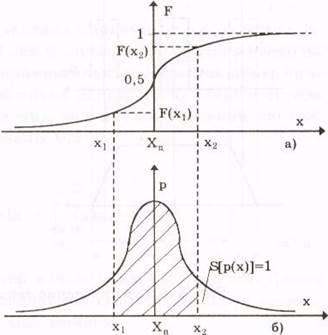
Ин­тегральной функцией распределения F(х) называют функцию, ка­ждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина хi {-∞ < хi ≤ +∞} в i-м опыте принимает значение, меньше х:

 

F(х) = Р{хi < х} = P{-∞ < хi ≤ х}. (1)

 

График интегральной функции распределения показан на рис 2. Она имеет следующие свойства:

• неотрицательная, т.е. F(х)≥0;

• неубывающая, т.е. F(х2)≥ F(х1), если х2 ≥ х1;

• диапазон ее изменения простирается от 0 до 1, т.е. F(-∞) = 0; F(+∞) = 1;

• вероятность нахождения случайной величины х в диапазоне от х1, до х2 Р{х1 < х < х2} = F(х2)- F(х1).

 

Более наглядным является описание свойств результатов изме­рений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей р(х)=dF(х)/dx. Она всегда неотрицательна и подчиняется условию нормирования в виде:

 

Учитывая взаимосвязь F(х) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х1; х2)

Следовательно, рассмотренное выше условие нормирования оз­начает, что вероятность попадания величины х в интервал [-∞; +∞] равна единице, т.е. представляет собой достоверное событие.

Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (х1;х2) равна площади, заключенной под кривой р(х) между абсциссами х1 и х2, (см. рис. 2). Поэто­му по форме кривой плот­ности вероятности р(х) можно судить о том, какие значения случайной вели­чины х наиболее вероятны, а какие наименее.

Результирующая по­грешность зачастую скла­дывается из ряда состав­ляющих с различными плотностями распределе­ния р1(х), р2,(х),..., рn(х).

В связи с этим возникает за­дача определения суммар­ного закона распределения погрешности.

Для суммы независимых непрерывных случайных величин х1, и х2, имеющих распределения р1(х1) и р2(x2), он называется композицией и выражается интегралами свертки:

 

Z = x1 (+) x2

 

Поделиться:

Воспользуйтесь поиском по сайту: