 |
Владимира Сергеевича Артамонова
|
|
|
|
Задания на контрольную работу № 1
Методические указания и контрольные вопросы по курсу
«Начертательная геометрия»
Санкт - Петербург
Рецензенты:
И.А. Шумейко
кандидат технических наук, доцент
(Санкт-Петербургский Государственный технологический университет растительных полимеров);
А.Н. Иванов
кандидат технических наук
(Санкт-Петербургский университет ГПС МЧС России)
Грачев Е.В., Бачурихин H.H, Груданова О.В., Королева И.В. Задания на контрольную работу № 1: Методические указания и контрольные вопросы по курсу «Начертательная геометрия». / Под ред. В.С. Артамонова. – СПб.: Санкт-Петербургский университет ГПС МЧС России, 2009. – 23 с.
Задания на контрольную работу № 1 методические указания и контрольные вопросы по первому разделу составлены в соответствии с учебной программой дисциплины «Начертательная геометрия. Инженерная графика» и предназначена для слушателей заочного обучения УГПС МЧС России. Задания, методические указания и контрольные вопросы позволяют обучающимся усовершенствовать свои знанияв теории построения чертежа и показать уровень усвоения учебного материала.
© Санкт-Петербургский университет ГПС МЧС России, 2009
Введение
Самоконтроль усвоения учебного материала осуществляется при решении рекомендованных программой и методическими указаниями задач и ответов на задачи ивопросы. Текущий контроль преподавателя за работой слушателя-заочника производится по контрольным работам, выполняемым слушателем после изучения соответствующие разделов и тем.
Выполненная слушателем контрольная работа №1 по теории построения чертежа должна содержать эпюры (чертежи) решённых задач и пояснительные записи к ним.
|
|
|
Эпюры контрольных работ выполняются на листах чертежной бумаги формата А4 или A3 и оформляются в соответствии с ГОСТ 2.301-68, ГОСТ 2.302-68, ГОСТ 2.303-68, ГОСТ 2.304-81. Каждый эпюр сопровождается пояснительной запиской, в которой на листе писчей бумаги формата А4 кратко излагаются планы решения задач и последовательность графических построении. Первая страница контрольной работы (титульный лист) выполняется по образцу, выдаваемому на установочном сборе.
Задания на контрольные работы индивидуальные. Слушатель выполняет тот вариант задания, номер которого соответствует сумме двух последних цифр его кода. Если код слушателя 9527, то он в заданиях КР 1 выполняет 9 вариант задания.
Эпюры задач вычерчиваются в заданном масштабе и размещаются в пределах формата листа. Эпюры выполняются c помощью чертежных инструментов карандашом 2T или 2H. Необходимо аккуратно выполнять построения, чтобы избежать неверных результатов. При обводке выполненных чертежей толщина линии принимается в соответствии с ГОСТ 2.303-68. Все видимые линий - сплошной основной линией, линии проекционной связи и линии построений - тонкие сплошные, линии центров и осевые - тонкие штрихпунктирные. Линии невидимых контуров показывать штриховыми линиями. Надписи выполняются стандартным шрифтом размером 3,5 и 5 в соответствии сГОСТ 2.304-68.
Контрольные работы представляются на рецензию в сроки, указанные в учебном графике, в полном объеме (все эпюры и пояснения к ним). Контрольную работу вместе с рецензией возвращают cлушателю, и она хранится у него до экзамена. Замечания преподавателя должны быть приняты слушателем к исполнению. Если работа не зачтена или зачтена не полностью, то на повторную рецензию надо представить снова всю контрольную работу. При сдаче зачета или экзамена слушатель представляет все контрольные работы и рецензии к ним.
|
|
|
Задача 1
Построить линию пересечения треугольников АBС и EDK. Показать видимость их на проекциях. Определить натуральную величину треугольника ABC.
Данные своего варианта выбираются из таблицы 1. Пример выполнения задачи приведен на рисунке 1. Работу выполнять на листе формата А3.
Рекомендации по решению задали 1
На левой половине листа построить оси проекций. По сумме последних двух цифр кода из таблицы 1выбирается номер варианта и соответствующие ему координаты точек A, B, C, D, E, К. По этим координатам определяется положение проекций вершин треугольников (рис. 1) на эпюре. Стороны треугольников и другие вспомогательные линии проводится тонкими сплошными линиями.
Линия пересечения плоскостей треугольников - прямая сплошная. Для ее определения достаточно определить две точки, принадлежащие одновременно двум заданным треугольникам. Задача в такой постановке имеет несколько равнозначных решений. Можно такую линию пересечения построить по точкам пересечений сторон одного треугольника с плоскостью другого. Можно использовать вспомогательные секущие проецирующие плоскости. Можно построить следы плоскостей. Можно решать задачу преобразованием плоскостей проекций. Анализ возможных путей решения поставленной задачи показывает, что первый наиболее рационален. Именно так построены проекции линий пересечения плоскостей треугольников в приведенном примере.
Видимость сторон пересекающихся треугольников определяется с помощью конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными основными линиями, а невидимые - штриховыми линиями.
Натуральная величина треугольника ABC определяется путем преобразования проекций. Вданном случае наиболее удобен способ плоскопараллельного перемещения треугольника ABC. В треугольнике ABC надо показать линию его пересечения с треугольником EDK.
После выполнения построений необходимо обвести все линии, буквы, цифры и надписи в соответствий с назначением и требованиями ГОСТа.
Заканчивается выполнение работы заполнением основной надписи.
Таблица 1. Данные к задаче 1 (размеры и координаты, мм)
| № вари-анта | xA | yA | zA | xB | yB | zB | xC | yC | zC | xD | yD | zD | xE | yE | zE | xK | yK | zK |
|
|
|

Рис. 1
Задача 2
Через прямую DE провести плоскость, перпендикулярную плоскости треугольника АВС. Построить линию переселения этик плоскостей и определить их видимости. Определить расстояние от точки D до плоскости треугольника ABC.
Данные для своего варианта взять из таблицы N2 по последней цифре кода.
Пример выполнения задачи приведён на рисунке 8.
Работу выполнять на листе формата А4.
Решение задачи следует начинать с анализа условий и возможных путей решения.
|
|
|
Чтобы построить плоскость, перпендикулярную другой плоскости, надо провести её через перпендикуляр к этой плоскости. Кроме того, искомая плоскость должна содержать в себе и заданную прямую. Следовательно, первое, что потребуется выполнить - это построить перпендикуляр к плоскости ABC, опущенный ив любой точки прямой DE (например из точки D). Плоскость, проходящая через перпендикуляр и прямую DE и будет искомой.
Перпендикуляр ив точки D к плоскости треугольника ABC можно провести используя горизонталь и фронталь, так как горизонтальная проекция, перпендикуляра перпендикулярна горизонтальной проекций горизонтали, а фронтальная проекция перпендикулярна фронтальной проекции фронтали.
Линию пересечения плоскости треугольника ABC ипостроенной перпендикулярной к ней можно построить, как в первой задаче, или любым другим способом.
Видимость плоскостей устанавливают с помощью конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям.
Определить расстояние от точки D до плоскости треугольника ABC можно способом прямоугольного треугольника (на эпюре не показано).
Таблица 2
| № вари-анта | Значения координат, мм | ||||||||||||||
| xA | yA | zA | xB | yB | zB | xC | yC | zC | xD | yD | zD | xE | yE | zE | |
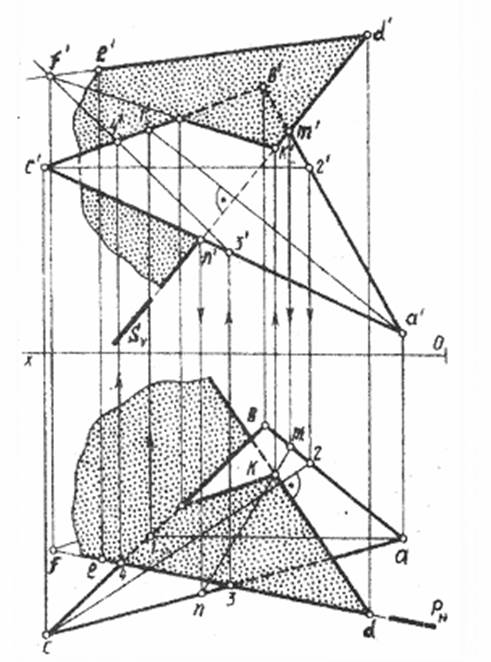
Рис. 2
Задача 3
Определить точки пересечения прямой линии с поверхностью пирамиды.
Данные для своего варианта ваять из таблицы 3. Пример выполнения задачи приведён на рисунке 3. Работу выполнять на листе формата А4.
Рекомендации по решению задачи
По координатам, взятым из таблицы для своего варианта, на эпюре обозначают проекции точек А, В, С, D, S и отроят проекции пирамиды SABCD. Затем строят проекции прямой линии МN.
Решение задачи выполняется в три этапа.
1. Через прямую MN проводят вспомогательную проецирующую плоскость Т.
2. Определяют проекции линии пересечения вспомогательной проецирующей плоскости с поверхностью пирамиды (в примере линия 1 2 3 4 1).
|
|
|
3. Находят точки пересечения проекции прямой MN с проекциями линий пересечения поверхности пирамиды и вспомогательной плоскости.
В заключение определяют видимость прямой и видимые отрезки проводят сплошной основной линией, а невидимые - штриховой.
Задача может иметь одно из трёх решений: прямая пересекает поверхность пирамиды в двух точках, в одной точке (касается) или не пересекает поверхность.
Таблица 3 Данные к задаче 3 (размеры и координаты, мм)
| № вари-анта | xA | yA | zA | xB | yB | zB | xC | yC | zC | xD | yD | zD | xs | ys | zs | xM | yM | zM | xN | yN | zN |
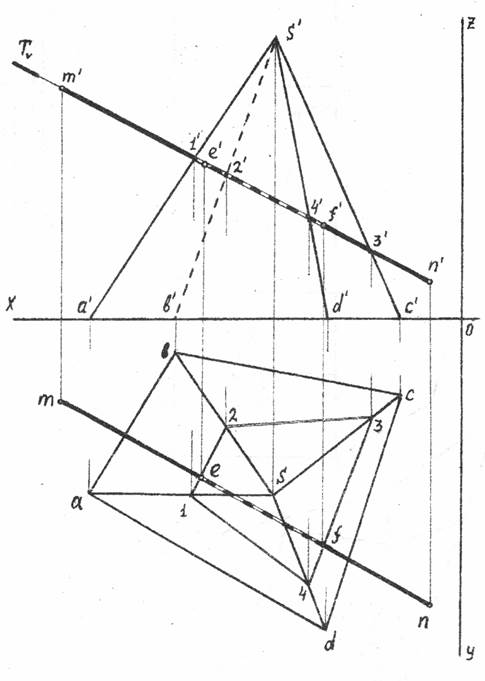
Рис.3
Задача 4
Построить линию переселения пирамиды с прямой призмой.
Данные своего варианта взять из таблицы 4.
Пример выполнении задачи приведен на рисунке 4.
Работу выполнять на листе формата А4.
Выполнение задания начинают с построения координационных осей X, Y, Z так, чтобы размеры фронтальной и горизонтальной плоскостей проекций были примерно одинаковы. Затем, по числовым значениям координат, которые берутся из таблицы в соответствии с номером варианта, строятся проекции точек А, В, С, D и соединяются тонкими линиями. Таким образом получают две проекции пирамиды. После этого обозначают проекции точек E, G, K, U. На горизонтальной плоскости проекции последовательно соединяют проекции точек k, g, u, е тонкими линиями, в результате чего образуется горизонтальная проекция основания призмы. Фронтальную проекцию приемы получают путём построения перпендикуляров к оси X в точках e1, k1, u1, g1 высотой h, которые являются проекциями боковых рёбер призмы. Невидимые рёбра проводятся штриховыми линиями. Соединяя концы крайних проекций ребер призмы прямой линией, параллельной оси X, получают фронтальную проекцию верхнего основания призмы.
Построение линии пересечения гранных тел можно осуществить двумя путями. Либо определить точки пересечения рёбер одного многогранника с гранями другого и рёбер второго с гранями первого, либо построить линии пересечения граней, как плоскостей, одного многогранника с гранями другого. Выбор пути решения делается после анализа условий задачи.
Анализ условий данной - задачи показывает, что боковые грани призмы являются горизонтально проецирующими плоскостями. Поэтому горизонтальные проекции точек - пересечения пирамиды ABCD с гранями призмы ЕКGU определяются чрезвычайно просто. Точнее, они становятся известными уже в процессе построения задания. Это точки 1, 2, 3, 4, 5, 6, 7, 8. Из этого следует, что и горизонтальные проекции линии пересечения пирамиды с призмой тоже известны. Это проекции граней призмы в пределах контура пирамиды - линия 1, 2, 3, 1 и линия 4, 5, б, 7, 8, 4.
Таким образом, после анализа условии задачи решение задачи сводится к построению фронтальных проекций точек 1, 2, 3, 4, 5, 7 путём проведения линий проекционной связи до соответствующих фронтальных проекций рёбер пирамиды.
Остается определить точки пересечения ребра Е призмы с гранями пирамиды. Решение задачи на определение точки пересечения прямой линии с плоскостью известно.
В данном случае, для упрощения решения, вспомогательную горизонтально проецирующую плоскость S целесообразно провести через ребро Е и вершину пирамиды D. На горизонтальной плоскости проекций горизонтальный след этой плоскости Sн изобразится прямой линией, проходящей через точки е и d.
Второй шаг алгоритма определения точки пересечения прямой с плоскостью заключается в определении линии пересечения заданной и вспомогательной плоскостей. Горизонтальные проекций линий пересечения граней пирамиды DBC и DAB со вспомогательной плоскостью Sн в данном случае совпадают с горизонтальным следом вспомогательной плоскости Sн. Отсюда следует, что отрезок прямой линии dn есть горизонтальная проекция линии пересечения грани DВС со вспомогательной плоскостью S. Фронтальная проекция линии пересечения этих плоскостей проходит через фронтальные проекции точек d’ и n’.
Третий шаг алгоритма определения точки пересечения прямой с плоскостью это определение точки пересечения заданной прямой линии с линией пересечения плоскостей. В данном случае легко убедиться, что фронтальная проекция ребра призмы е’ пересекается с фронтальной проекцией линии пересечения граней DBC и вспомогательной плоскости S - линией d’n’ в точке 6’. В точке 6 (её проекции 6 и 6') ребро Е пересекается с гранью DBC. Аналогично определяется и фронтальная проекция точки В - точке 8’.
Затем соединяют фронтальные проекции точек пересечения рёбер с гранями в правильной последовательности прямыми линиями. При выполнении этой части задачи надо убедиться, что соединяемые точки принадлежат одной грани, а последовательность определяется их положением на горизонтальной проекции линии пересечения. Например, точки 5, 6, 7 принадлежат одной грани DBC, так как точка 5 находится на ребре DС, точка 6 на линии DN, точка 7 на ребре DB. Через эти точки и надо провести прямые, но нельзя соединять прямой точки 5' и 7’, потому что на горизонтальной проекции линии пересечения этого отрезка нет. А есть отрезки 5-6 и 6-7. Следовательно, на фронтальной плоскости проекции надо соединить прямыми линиями точки 5’ и 6’, а затем точки 6’ и 7 '. Подобным образом строятся и другие проекции отрезков ломаной замкнутой линии пересечения этих гранных плоскостей.
После построения фронтальной проекции линии пересечения призмы к пирамиды необходимо определить видимость отрезков этой ломаной линии с помощью конкурирующих точек. Видимые отрезки прямых линий надо провести сплошной основной линией, а невидимые штриховой. Линии проекционной связи и другие вспомогательные линии - тонкими сплошными линиями. Точки желательно изобразить кружками, которые легко выполнить с помощью балеринки.
Заканчивая работу, следует проверить результаты решения задачи и заполнить основную надпись. Надо иметь в виду, что от правильности решения этой задачи зависят результаты выполнения следующей задачи.

Рис. 4
Таблица 4 Данные к задаче 4 (координаты и размеры, мм)
| № вари-анта а | xA | yA | zA | xB | yB | zB | xC | yC | zC | xD | yD | zD | xS | yS | zS | xM | yM | zM | xN | yN | zN | xE | yE | zE | A |
Задача 5
Построить развертки пересекающихся многогранников - прямой призмы с пирамидой, линию пересечения которых определяли в задаче 4. На развертках показать линию их пересечения.
Пример выполнения задачи приведен на рис. 5
Работу выполнять, на листе формата A3.
Указания к решению задачи 5.
Проекции пересекающихся многогранников, которые были построены в задаче 4, надо перевести на кальку формата A3. На этой кальке выполняются вспомогательные построения для определения натуральных размеров рёбер многогранников. Сами развёртки многогранников строятся на листе ватмана формата A3.
Развёртку призмы можно получить различными способами. В данном случае, ввиду того, что призма прямая, можно выполнять развёртку в следующей последовательности:
а) Провести горизонтальную прямую;
6) От произвольной точки G этой прямой отложить отрезки GU, UE, ЕК, КG, равные длинам сторон основания призмы;
в) Из точек G, U, E, K, G провести перпендикуляры к прямой G -G, равные высоте призмы, и соединить их концы прямой линией, параллельной G -G. Прямоугольник GG1G1G является разверткой боковой поверхности призмы.
г) К развёртке боковой поверхности призмы пристраивают многоугольники её оснований.
При построении наразвертке линии пересечения приемы с пирамидой, состоящей из замкнутых ломаных линий 123 и 45678, используют вертикальные прямые. Например, для определения положения
точки 1 на развёртке поступают так: на отрезке gu от точки G вправо откладывают отрезок G10, равный отрезку G1 на горизонтальной проекции пересекающихся многогранников (задача 4). Из точки 10 проводят перпендикуляр к отрезку GU и на нем откладывают аппликату точки 1 с фронтальной проекции пересекающихся призмы и пирамиды. Остальные точки строятся аналогично.
Развертка пирамиды выполняется после определения натуральных размеров ребер, которое производилось на кальке. Намечают положение вершины пирамиды D, проводят ребро DA или любое другое, cтроят грань DАC, затем грань DBC и т.д. К одному из ребер основания пристраивают многоугольник основания. На ребрах и гранях пирамиды (на развертке) определяют положение вершин пространственной ломаной линии пересечения пирамиды с призмой.
Листы с планом решения задачи и кальку с результатами определения натуральных величин ребер многогранников представлять вместе с чертежами.
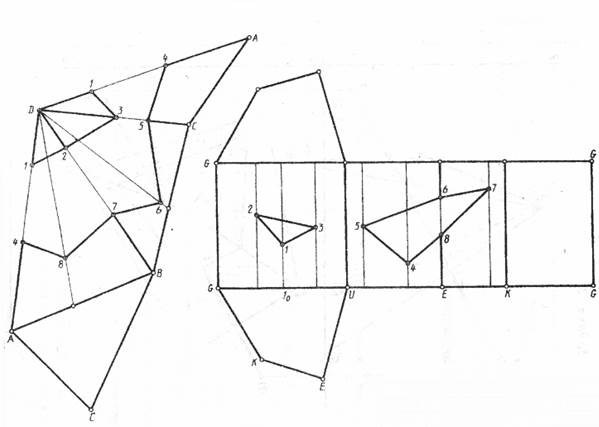
Рис. 5
Задача 6
Построить линию пересечения конуса вращения плоскостью ABC общего положения.
Данные для своего варианта взять из таблицы 5
Пример выполнения задачи приведен на рис.6.
Работу выполнять на листе формата A3 совместно с задачей 7 или отдельно на формате А4.
Указания к решению задачи
В левой половине листа формата A3 намечаются оси координат. Из таблицы 5 согласно своему варианту берутся величины, которыми задаются на эпюре поверхность конуса вращения и плоскость ABC.
Определяется центр (точка К) и проводится окружность радиуса R основания конуса вращения в плоскости уровня. На расстоянии h от точки К (на фронтальной плоскости проекций) отмечается вершина конуса S. Строится фронтальная проекция конуса. По координатам определяется положение проекций точек А, В и С. Для наглядности проекции точек соединяются прямыми линиями. Получается, что секущая плоскость задается прямыми АВ и ВC.
Наиболее простой путь решения задачи заключается в применении одного из способов преобразования проекций с целью преобразования секущей плоскости в проецирующую. В примере использован способ замены плоскостей проекций.
Новую фронтальную плоскость проекции V1 ставят перпендикулярно секущей плоскости ABC. Это достигается тем, что новую ось проекций X, располагают перпендикулярно горизонтальной проекции горизонтали плоскости ABC. Тогда не плоскости проекции V1 секущая плоскость ABC проецируется в виде прямой линии, а проекция линии пересечения конуса плоскостью - в виде отрезка этой прямой в пределах контура конуса (отрезок 11 21).
Сечение конуса плоскостью пол углом к оси конуса представляет собой эллипс. Имея проекцию сечений конуса плоскостью АВС на дополнительной плоскости проекций V1, строят основные проекции сечения на плоскостях H, V, где линия пересечения будет эллипсом.
Таблица 5 Данные к задаче 6 (координаты и размеры, мм)
| № вари-анта | xk | yk | zk | xA | yA | zA | xB | yB | zB | xC | yC | zC | R | h |
|
|
|


