Задача 4. Определение кинематических характеристик плоского движения

 

Кривошип OA длиной 0,2 м вращается рав­номерно с угловой скоростью ω_OA = 10 с^–1 и при­водит в движение шатун АВ длиной 1 м. Пол­зун В движется по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также скорость и ускорение ползуна в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с вертикалью угол 45° (рисунок 16.1).

Решение.

1. Определение скоростей. Вычис­лим скорость точки А как точки вра­щающегося кривошипа:

.

 

Она направлена перпендикулярно ОА (рисунок 17.1).

 

 

Рисунок 16.1 Рисунок 17.1 Рисунок 18.1

 

Скорость v_B ползуна направлена по направляющей вертикально.

Для шатуна АВ, совершающего плоское движение, теперь известны направления скоростей двух его то­чек: А и В. Восставляя перпендику­ляры к векторам этих скоростей, на­ходим точку Р их пересечения — МЦС шатуна.

Используя известную формулу для скоростей точек при плоском движении, получаем ; .

Из треугольника АВР имеем | АР | = 1 м; | ВР | = м, и тогда

 

.

 

2. Определение ускорений. Вычислим сначала ускоре­ние точки А как точки кривошипа: .

Здесь вращательное ускорение , так как , поскольку .

Тогда полное ускорение точки А равно центростремительному

и направлено к оси вращения — точке О (рисунок 18.1).

Для вычисления ускорения точки В воспользуемся тео­ремой о сложении ускорений, взяв точку А в качестве полюса:

. (1)

Центростремительное ускорение точки В в относи­тельном вращении вокруг точки А по модулю равно , и направлено от точки В к полю­су — точке А.

Модуль вращательного ускорения определяется по формуле 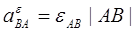и пока не может быть вычислен, поскольку неизвестна величина углового ускорения . Направление вектора также не может быть определе­но однозначно, так как неизвестно направление углового ускорения, т. е. неизвестно, ускоренным или замедлен­ным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление совпадет с направле­нием , а вектор направим перпендикулярно от­резку ВА по ходу углового ускорения.

Вектор ускорения точки В направлен по вертикальной прямолинейной направляющей. Будем пока считать дви­жение ползуна ускоренным и направим ускорение в ту же сторону, что и скорость (рисунок 17.1, 18.1).

Теперь в равенстве (1) все ускорения имеют определен­ное направление, и мы можем записать это уравнение в проекциях на выбранные оси:

 

.

 

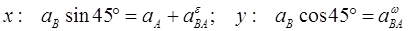Из последнего уравнения получаем , тогда из первого уравнения

.

Отсюда следует, что

.

Отрицательные знаки у величин и показывают, что их истинные направления противоположны принятым.

 

№ вар.	ОА	АВ	α	ωOA
	0,5	1,1
	0,4	1,2
	0,3	1,3
	0,2	1,4
	0,95	1,5
	0,85	1,6
	0,75	1,7
	0,65	1,8
	0,55	1,9
	0,45
	0,35	1,1
	0,25	1,2
	0,9	1,3
	0,8	1,4
	0,7	1,5
	0,6	1,6
	0,5	1,7
	0,4	1,8
	0,3	1,9
	0,2	1,9

 

 

Вопросы для защиты задачи

 

1. Какое движение тела называется плоским и как оно задается?

2. Как определить скорость любой точки плоской фигуры?

3. Способы определения мгновенного центра скоростей.

4. Как определить скорость любой точки плоской фигуры, если известен мгновенный центр скоростей?

5. Как определить ускорение любой точки плоской фигуры

Третий раздел теоретической механики «Динамика»

Задача 5.Динамика точки.

 

Материальной точке сообщается начальная скорость v ₀ = 7 м/с, в результате чего она проходит по горизон­тальной шероховатой плоскости расстояние l = 10,1 м и падает с нее. Коэффициент трения скольжения f = 0,2. Определить скорость v, длину полета L, глубину падения Н точки в мо­мент t = 5 с после начала движения. Сопротивление среды не учитывать (рис. 51).

 

Рис. 51 Рис. 52

 

Решение. Рассмотрим движение точки на прямолинейном участке АВ (рис. 52). Определим скорость точки в кон­це этого участка. Начало осей коор­динат совместимо с началом движе­ния. Начальные условия при t = 0 имеют вид

 

 

На основании принципа освобождаемости от связей рассматриваем точку как свободную, на которую действует сила тяжести mg, нормальная ре­акция N и сила трения F_mp.

Дифференциальные уравнения движения материаль­ной точки в декартовых осях:

,

 

в данном случае с учетом того, что и 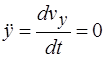, принимают вид

 

 

Отсюда N = mg. Используя закон Кулона для силы трения F_mp = fN, получаем F_mp = fmg. Тогда

. (*)

 

Разделим переменные t и v_x в уравнении (•) и проин­тегрируем его, пользуясь неопределенными интегралами

 

.

 

Учитывая начальное условие, определим постоянную интегрирования С ₁ = v ₀. Тогда формула изменения скоро­сти точки на участке АВ принимает вид

 

. (**)

 

Если же пользоваться определенными интегралами, то необходимость в постоянной интегрирования отпадает. Из (*) получаем

 

.

 

Здесь нижние пределы интегралов соответствуют на­чальным условиям, а верхние — произвольному моменту времени.

Из последнего уравнения находим , дела­ем подстановку и получаем то же решение: .

Для того чтобы вычислить время t ₁ преодоления ма­териальной точкой пути АВ и ее скорость в момент про­хождения точки В, необходимо использовать условие | АВ | = l = 10,1 м.

При этом возможны два варианта дальнейшего реше­ния задачи.

1. Перепишем уравнение (**), учитывая, что v_x =dx/dt,

 

.

 

Разделив здесь переменные и проинтегрировав (напри­мер, с использованием определенных интегралов) это уравнение, получим

 

,

откуда

.

 

Из последнего уравнения можно определить время, когда величина х будет равна l. Решая квадратное уравне­ние или , отыски­ваем два значения: t с и t₁ = 5,1 с. Второе значение времени физически не реализуется, так как предполагает дальнейшее движение точки по горизонтали, а затем воз­врат ее в точку B, что невозможно, поскольку после точки В материальная точка перестает взаимодействовать с по­верхностью и начинает падать.

Таким образом, время t ₁= 2 с и, подставляя его в фор­мулу (**), находим скорость точки в конце участка АВ: м/с.

 

Рассмотрим далее криволи­нейное движение точки на участ­ке ВС (рис. 53). Начало отсчета времени совме­стим с моментом начала падения. Начальные условия в выбранных осях координат принимают вид:

при t = 0

х = 0; = 3,1 м/с; у = 0; = 0.

 

Рис. 53

 

На точку действует только сила тяжести mg. Запи­шем дифференциальные уравнения движения точки:

,

или

.

 

Разделив переменные и проинтегрировав эти уравне­ния, получим

 

v_x = C ₃; v_y = gt + C ₄.

 

В соответствии с начальными условиями постоянные интегрирования равны С ₃ = v ₁ и С ₄ = 0.

Тогда имеем v_x = v ₁ = const, v_y = gt.

Рассматриваемое время свободного падения точки, от­считываемое от положения В, равно t ₂ = t – t ₁ = 3 с.

Вычислим скорость v ₂ точки в момент t ₂ = 3 с (поло­жение С на траектории)

v _{2 x} = v ₁= 3,1 м/с; v _{2 y} = gt ₂ = 29,4 м/с;

м/с.

Дифференциальные уравнения движения точки на уча­стке ВС представим в следующем виде:

.

 

Разделяя переменные и интегрируя эти уравнения, получаем

.

 

Постоянные интегрирования определяем по заданным начальным условиям (при t = 0 х = 0; у = 0), а именно: С ₅ = С ₆ = 0.

Уравнения движения точки имеют вид х = v ₁ t, у = gt ²/2.

При заданном t ₂ = 3 с находим дальность полета L = x (t ₂) = 9,3 м и глубину падения Н = y (t ₂) = 44,1 м.

Ответ: v = 29,6 м/с; L = 9,3 м; Н = 44,1 м.

№ вар.	v 0	l	f	t
			0,2.
		8,1	0,2.
		8,2	0,2.
		8,3	0,2.
		8,4	0,2.
		8,5	0,2.
		8,6	0,2.
		8,7	0,2.
		8,8	0,2.
		8,9	0,2.
			0,2.
		9,1	0,2.
		9,2	0,2.
		9,3	0,2.
		9,4	0,2.
		9,5	0,2.
		9,6	0,2.
		9,7	0,2.
		9,8	0,2.
		9,9	0,2.

Вопросы для защиты задачи

 

1. Сформулируйте законы динамики.

2. Запишите дифференциальные уравнения движения матери­альной точки в проекциях на оси прямоугольной декартовой системы координат.

3. Запишите дифференциальные уравнения движения материальной точки в проекциях на естественные оси.

4. Сущность первой задачи динамики и порядок ее решения.

5. Сущность второй задачи динамики и порядок ее решения.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: