 |
Математическое ожидание функций дискретных случайных переменных
|
|
|
|
Пусть g(x) – некоторая функция от Х. Тогда ее математическое ожидание будет иметь вид:
Вернемся к примеру с игральными костями. Пусть 
.
| Х | р | g(X) | g(X)p | Х | р | X2 | X2p |
| х1 | p1 | g(х1) | g(х1)p1 | 1/36 | 4/36 | ||
| х2 | p2 | g(х2) | g(х2)p2 | 2/36 | 9/36 | ||
| х3 | p3 | g(х3) | g(х3)p3 | 3/36 | 16/36 | ||
| … | … | … | … | 4/36 | 25/36 | ||
| … | … | … | … | 5/36 | 36/36 | ||
| … | … | … | … | 6/36 | 49/36 | ||
| … | … | … | … | 5/36 | 64/36 | ||
| … | … | … | … | 4/36 | 81/36 | ||
| … | … | … | … | 3/36 | 100/36 | ||
| … | … | … | … | 2/36 | 121/36 | ||
| xn | pn | g(xn) | g(xn)pn | 1/36 | 144/36 | ||
|
Задание 5. Рассчитайте математическое ожидание E(X2) для случайной величины Х в задании 1
Решение
| Х | р | X2 | X2p |
| 6/36 | |||
| 10/36 | 10/36 | ||
| 8/36 | 32/36 | ||
| 6/36 | 54/36 | ||
| 4/36 | 64/36 | ||
| 2/36 | 50/36 | ||
|
Задание 6. Рассчитайте математическое ожидание E(X2) для случайной величины Х в задании 2
Решение
| Х | р | X2 | X2p |
| 1/36 | 1/36 | ||
| 3/36 | 12/36 | ||
| 5/36 | 45/36 | ||
| 7/36 | 112/36 | ||
| 9/36 | 225/36 | ||
| 11/36 | 396/36 | ||
|
Свойства математического ожидания
1. 
2. 
3. 
4. 
Пусть 
, тогда 
.
Задание 7. Пусть Х – сумма очков, выпавшая при бросании двух костей. Рассчитайте возможные значения для Y, если 
и далее рассчитайте E(Y). Покажите, что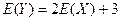 
.
Решение
 Зел.
Кр.
| ||||||
| Х | р |
| Yp |
| 1/36 | 7/36 | ||
| 2/36 | 18/36 | ||
| 3/36 | 33/36 | ||
| 4/36 | 52/36 | ||
| 5/36 | 75/36 | ||
| 6/36 | 102/36 | ||
| 5/36 | 95/36 | ||
| 4/36 | 84/36 | ||
| 3/36 | 69/36 | ||
| 2/36 | 50/36 | ||
| 1/36 | 27/36 | ||
|
|
|
|
Для оценки колеблемости значений признака относительно средней используются характеристики рассеяния. Они различаются формой средней и способами оценки отклонений от ее отдельных вариантов. К таким показателям относят: среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
_______________________________________________________________________
Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений отдельных вариантов от их средней величины:
_______________________________________________________________________
Среднее линейное отклонение выражено в тех же единицах измерения, что и варианты или их средняя. Оно дают абсолютную меру вариации. Чтобы избежать равенства нулю суммы отклонений, используют либо абсолютные значения отклонений, либо их четные степени, например квадраты. В последнем случае мера вариации называется дисперсией и обозначается 
.
Дисперсия генеральной совокупности дискретных случайных величин является полезной мерой разброса вероятностного распределения. Она определяется как математическое ожидание квадрата разности между величиной Х и ее средним, т.е. 
, где 
– среднее генеральной совокупности.
Применительно к примеру с игральными костями:
| Х | р | 
|
| 
|
| 1/36 | -5 | 25/36 | ||
| 2/36 | -4 | 32/36 | ||
| 3/36 | -3 | 27/36 | ||
| 4/36 | -2 | 16/36 | ||
| 5/36 | -1 | 5/36 | ||
| 6/36 | ||||
| 5/36 | -1 | 5/36 | ||
| 4/36 | -2 | 16/36 | ||
| 3/36 | -3 | 27/36 | ||
| 2/36 | -4 | 32/36 | ||
| 1/36 | -5 | 25/36 | ||
Дисперсия 
Стандартное отклонение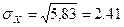 
|
_______________________________________________________________________
Среднее квадратическое отклонение – это арифметическое значение корня квадратного из ее выборочной дисперсии:
_______________________________________________________________________
Среднее квадратическое отклонение показывает, насколько в среднем отклоняются конкретные значения признака от их среднего. Выражаются в единицах измерения, поэтому легко интерпретируются. Большое значение среднего квадратического отклонения показывает большой разброс значений в представленной совокупности по сравнению со средним по выборке значением.
|
|
|
_______________________________________________________________________
Выборочной дисперсией (вариацией) называется среднее арифметическое квадратов отклонений наблюдаемых значений случайной величины от выборочного среднего значения:
_______________________________________________________________________
Причина вариации – различные условия существования отдельных единиц совокупности.
Свойства вариации:
1) если 
, то 
2) если 
, то 
3) 
4) если 
, то 
Дисперсия характеризует отклонение (разброс, рассеяние, вариацию) значений переменной относительно среднего по выборке значения / ожидаемого значения. Дисперсия характеризует колеблемость / изменчивость случайной величины. Чем больше вариация, тем дальше от средней находятся возможные значения случайной величины.
Если сравниваются две случайные величины, то из них, которая имеет большую дисперсию и большее среднее квадратическое отклонение, более вариабельна.
Задание 8. Дисперсия случайной величины Х равна 8. Найти дисперсию следующих величин: 1) Х–4; 2) -9Х; 3) 4Х–3.
Решение
(Х) = 5
(Х–4) = (Х) + (-4) = 5–0=5
(-9Х) = 81 (Х) = 81х5 = 405
(4Х–3) = 16 (Х) + (-3) = 80.
_______________________________________________________________________
Коэффициент вариации – это отношение среднего квадратического отклонения к среднему значению по выборке, выраженное в процентах:
_______________________________________________________________________
Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Для разных выборок, взятых в одной и той же генеральной совокупности, выборочные средние и выборочные дисперсии будут различны, т.е. выборочные характеристики являются случайными величинами.
Расчет коэффициентов корреляции основан на сумме произведений отклонений индивидуальных значений признаков 
и 
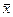от их средних значений 
и 
: 
. Эта величина, деленная на число единиц исследуемой совокупность n, называется ковариацией:
Свойства ковариации:
1) если , то 
2) если 
, то 
3) если , то 
Ковариация характеризует сопряженность вариации двух признаков, представляет собой статистическую меру взаимодействия двух случайных переменных и позволяет выразить связь одним числом.
|
|
|
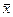При наличии прямой связи большие значения должны сочетаться с большими значениями , следовательно, отклонения в числители показателя будут положительными. Для малых значений и эти отклонения будут отрицательными, а их произведения положительными, следовательно, и ковариация будет величиной положительной. При наличии обратной связи отклонения значений и от их средних значений и будут иметь разные знаки, и ковариация будет представлена отрицательной величиной.
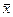При отсутствии связи сочетание знаков отклонений значений и от их средних значений и будет беспорядочным, при суммировании произведения отклонений взаимно погасят друг друга и ковариация будет близко к нулю.
Ковариация характеризует одновременно и степень зависимости переменных, и их рассеяние. Ковариация – величина размерная, т.е. измеряется в единицах измерения, что затрудняет ее использование для оценки степени зависимости переменных. Этих недостатков лишен коэффициент корреляции.
Задание 9. Имеются данные о расходах на продукты питания по 16 домохозяйствам:
| n | ||||||||||||||||
| X | 3,7 | 4,1 | 5,0 | 3,9 | 3,5 | 4,2 | 6,5 | 8,2 | 5,3 | 4,0 | 8,3 | 7,0 | 9,5 | 4,4 | 10,2 | 9,8 |
Необходимо рассчитать коэффициент вариации; среднее квадратическое отклонение и выборочную дисперсию (вариацию).
Решение
| n | S | Ср. | ||||||||||||||||
| X | 3,7 | 4,1 | 5,0 | 3,9 | 3,5 | 4,2 | 6,5 | 8,2 | 5,3 | 4,0 | 8,3 | 7,0 | 8,5 | 4,4 | 3,9 | 5,8 | 86,3 | 5,39 |
| -1,69 | -1,29 | -0,39 | -1,49 | -1,89 | -1,19 | 1,11 | 2,81 | -0,09 | -1,39 | 2,91 | 1,61 | 3,11 | -0,99 | -1,49 | 0,41 | ||
| 2,86 | 1,66 | 0,15 | 2,22 | 3,57 | 1,42 | 1,23 | 7,89 | 0,008 | 1,93 | 8,47 | 2,59 | 9,67 | 0,98 | 2,22 | 0,17 | 47,038 | 2,94 |
Вариация
= 2,94 (тыс. руб.) – чем больше вариация, тем дальше от средней находятся возможные значения случайной величины
Среднее квадратическое отклонение
= 
=1,71 (тыс. руб.) – показывает, насколько в среднем отклоняются конкретные значения признака от их среднего.
|
|
|
Коэффициент вариации
= (1,71/ 6,1) х 100 = 28,03 – так как коэффициент вариации не превышает 33%, то данная совокупность однородна.
|
|
|
