 |
Нормирование капиталовложений
|
|
|
|
До этого момента предполагалось, что фирма обладает достаточными фондами, чтобы инвестировать в любой проект, который имеет положительную NPV. Однако из-за внешних ограничений (жесткое нормирование) или внутренних факторов (мягкое нормирование) доступные фонды для инвестиций могут быть ограничены. В таком случае, выбор надо уже делать между проектами с положительной NPV.
Для этого более применим индекс рентабельности инвестиций (PI), чем оценка NPV. В то время, как NPV показывает стоимость инвестиций, PI выражает эту стоимость с позиции удельного веса необходимых первоначальных затрат. Таким образом, при нехватке фондов проект с более высоким PI был бы предпочтительнее, так как прибыль с каждого вложенного рубля будет больше, чем у проекта с низким PI.
Пример 6. Компания имеет 100 000$, которые она может инвестировать. Рассматриваются следующие инвестиционные проекты:
| Проект | IC | NPV | PI |
| A | 50 000 | 80 000 | |
| B | 30 000 | 45 000 | |
| C | 20 000 | 40 000 | |
| D | 30 000 | 42 000 | |
| E | 20 000 | 32 000 |
Какие проекты будут отобраны? Какая суммарная NPV будет получена?
Будут выбраны проекты в следующем порядке: C, A, E. Оставшиеся 10 000$ будут вложены в проект B. Суммарная NPV составит: ((40 000 + 80 000 + 32 000 + (45 000 / 3)) = 167 000).
| Проект | IC | NPV | PI |
| A | 50 000 | 80 000 | 1,6 |
| B | 30 000 | 45 000 | 1,5 |
| C | 20 000 | 40 000 | 2,0 |
| D | 30 000 | 42 000 | 1,4 |
| E | 20 000 | 32 000 | 1,6 |
Основное упрощение в этом примере состоит в том, что проекты делимы (как в случае с проектом B). На практике это не всегда так и не все доступные фонды могут быть потрачены, если выбраны только "целые" проекты. Столкнувшись с неделимыми проектами, возможны различные группировки, которые соответствуют бюджету расходов. Таким образом, инвестор должен собрать портфель проектов, выбирая такие, которые дают максимальную NPV.
|
|
|
Пример 7. Решим эту задачу, используя данные примера 6.
Возможные группировки проектов:
| Комбинации | NPV, тыс. $. | Общий NPV, тыс. $. |
| A, B, C | 80 + 45 + 40 | 165 |
| A, B, E | 80 + 45 + 32 | 157 |
| A, C, D | 80 + 40 + 42 | 162 |
| A, C, E | 80 + 40 + 32 | 152 |
| A, D, E | 80 + 42 + 32 | 154 |
| B, C, D, E | 45 + 40 + 42 + 32 | 159 |
Таким образом, там где нельзя выбрать проект B частично, наиболее предпочтительной является первая комбинация, хотя она и дает меньшую суммарную NPV, чем в примере 6.
Таким образом, в условиях нормирования капитала, выбор проектов с наибольшими PI обеспечит фирме максимальную NPV. В случае если проекты неделимы, метод "портфеля" используется для выбора лучшей группы проектов, хотя недостаток неделимости означает, что общая NPV не достигнет своего наибольшего возможного значения.
Более сложным методом отбора проектов при существовании одного или нескольких ограничений на объемы возможных инвестиций является линейное программирование (LP).
Линейное программирование – это метод пришедший из области операционных исследований и подразумевающий обычно использование вычислительной техники. С помощью этого метода можно вычислить оптимальные решения, когда цель (максимизация NPV) должна быть достигнута при соблюдении определенных условий (в нашем случае в условиях нормирования капитала). В более сложных формах линейное программирование может просчитать пути достижения множества целей при задании нескольких исходных условий, в том числе и ограничений с вероятностными исходами. Линейное программирование также применимо, когда инвестиционный проект должен удовлетворять требованиям по минимальной ликвидности (сроку окупаемости) и доходности.
Чтобы использовать линейное программирование, следует сформулировать ряд целей и ограничений, которые определяют необходимое количество информации для принятия решения. Определенным препятствием на пути применения LP является необходимость четкого определения значений ключевых переменных, влияющих на конечное решение.
|
|
|
Пример 8. У компании есть 3 инвестиционных проекта. NPV всех проектов положительна. Однако компания не может принять все проекты по причине недостаточности ресурсов. На этот и следующий год доступны по 200 000$, причем не потраченные суммы не могут быть перенесены на следующий год.
| Проект | NPV, тыс. $. | IC, тыс. $. | |
| в 1-ый год | во 2-ой год | ||
| X | 180 | 60 | 80 |
| Y | 370 | 100 | 100 |
| Z | 540 | 140 | 140 |
Данный пример может быть (в силу простоты) решен 2-мя путями:
а) путем ручного перебора всех комбинаций:
| Комбинация | Общая NPV, тыс. $ | IC, тыс. $. | Осуществимы? | |
| в 1-ый год | во 2-ой год | |||
| Один X | 190 | 60 | 80 | Да |
| Один Y | 370 | 100 | 100 | Да |
| Один Z | 540 | 140 | 140 | Да |
| X и Y | 550 | 160 | 180 | Да |
| X и Z | 720 | 200 | 220 | Нет |
| Y и Z | 910 | 240 | 240 | Нет |
| X, Y и Z | 1090 | 300 | 320 | Нет |
Заметим, что если рассматривается только текущий год, будет выбрана комбинация X и Z (требуемые капиталовложения 200 000$ и общая NPV – 720 000$). Но если принять во внимание следующий год, комбинация X и Z превышает допустимые фонды (требуемые капиталовложения 220 000$). Поэтому лучший вариант, который осуществим за 2 года – это комбинация X и Y проектов с суммарной NPV – 550 000$.
б) сформулировать задачу линейного программирования:
1) Цель (целевая функция) –  (максимизация значения NPV);
(максимизация значения NPV);
2) Ограничения:
·  (1-ый год);
(1-ый год);
·  (2-ый год).
(2-ый год).
3) Также необходимо наложить такие ограничения, чтобы ответы на эту задачу имели смысл. Для этого решения должны быть или "0", или "1". Не может быть отрицательных решений (нельзя инвестировать отрицательную сумму в проект), решения должны быть целыми числами (нельзя вложить в часть проекта) и решения не могут превышать "1" (нельзя инвестировать более одного раза в один и тот же проект). Поэтому вводятся следующие ограничения:
·  ;
;
·  ;
;
·  .
.
Сформулированная задача решается с помощью компьютерной программы (здесь используется MS Excel):
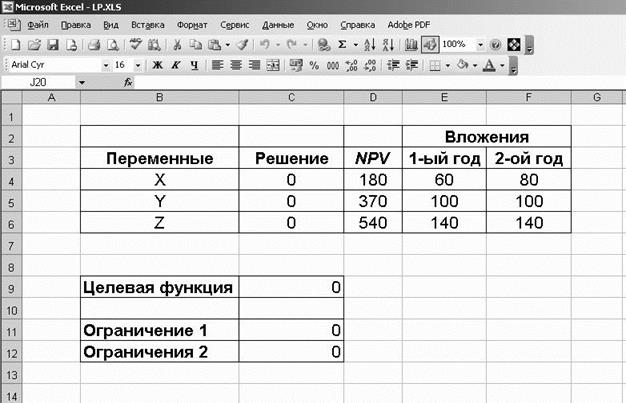
Рис. 10.1 Условие задачи примера 8[2]
Для решения задачи необходимо выполнить пункт меню "Сервис - Поиск решения" и заполнить необходимые пункты появившейся формы, после чего нажать "Выполнить":
|
|
|

Рис. 10.2 Использование поиска решения

Рис. 10.3 Решение примера 8
Результат решения задачи линейного программирования согласуется с вариантом ручного перебора всех возможных комбинаций проектов. В таком простом примере преимущества применения LP не столь очевидны, как в случае, если бы мы рассматривали множество проектов со множеством ограничений.
Контрольные вопросы:
1) Какое воздействие оказывает налогообложение на денежные потоки инвестиционного проекта?
2) Какое воздействие оказывает амортизация на денежные потоки инвестиционного проекта?
3) Как учитывается инфляция в инвестиционном проектировании?
4) Как соотносятся между собой реальная и номинальная ставка дисконтирования?
5) Как сравниваются проекты с разными сроками жизни? Раскройте содержание метода самовозобновления проекта.
6) Как сравниваются проекты с разными сроками жизни? Раскройте содержание метода эквивалентных годовых денежных потоков.
7) Как сравниваются проекты с разными сроками жизни? Раскройте содержание метода условной продажи более долгосрочного проекта.
8) В чем заключается проблема нормирования капиталовложений в инвестиционном проектировании?
9) Как для решения проблемы нормирования инвестиций используется индекс рентабельности?
10) Как формулируется задача линейного программирования для решения проблемы нормирования капиталовложений?
|
|
|


