 |
Общая постановка блочно-симметричных задач дискретного программирования
|
|
|
|
Ряд прикладных задач: проектирования модульного программного обеспечения и массивов базы данных информационных систем, распределение программных модулей и массивов базы данных по узлам вычислительных сетей, выбор проектов в условиях ограниченных ресурсов можно сформулировать в виде нового класса задач – блочно-симметричных моделей дискретного программирования. В отличие от традиционных моделей модели этого класса позволяют формулировать задачи с несколькими типами переменных различной природы, проводить декомпозицию сложных задач на блоки с единой целевой функцией и разрабатывать эффективные алгоритмы, имеющие полиномиальную вычислительную сложность.
Рассмотрим общую постановку блочно-симметричных задач дискретного программирования [126, 127].
Постановка задачи. Пусть задано множество объектов  и множество объектов
и множество объектов  с элементами различных типов, а также взаимосвязи между элементам этих множеств, которые определяются матрицей
с элементами различных типов, а также взаимосвязи между элементам этих множеств, которые определяются матрицей
 ,
,  ,
,  ,
,
Элементы которой целочисленные и булевы. Необходимо объединить элементы множество  в непересекающиеся подмножества
в непересекающиеся подмножества  , а элементы множества
, а элементы множества 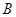 - непересекающейся подмножества
- непересекающейся подмножества  , таким образом, чтобы доставить экстремум целевой функции
, таким образом, чтобы доставить экстремум целевой функции  .
.
Для формализованной постановки задачи введем следующие переменные. Пусть  - булева матрица, где
- булева матрица, где  , если
, если  -й элемент распределяется в
-й элемент распределяется в  -ю группу,
-ю группу,  в противном случае. Аналогично
в противном случае. Аналогично  , где
, где  , если
, если  -й элемент распределяется в
-й элемент распределяется в  -ю группу и
-ю группу и  в противном случае. В общем случае матрицы переменных
в противном случае. В общем случае матрицы переменных  и
и  могут быть целочисленными [136].
могут быть целочисленными [136].
Определим на множестве  функцию
функцию  , зависящую от распределения элементов множеств
, зависящую от распределения элементов множеств  и
и 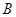 по подмножествам
по подмножествам  и
и  . Соответственно на множестве
. Соответственно на множестве  - функции
- функции  , а на множестве
, а на множестве 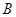 - функции
- функции  , определяющие ограничения на множествах
, определяющие ограничения на множествах  и
и 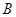 .
.
|
|
|
Блочно-симметричная задача дискретного программирования формулируется следующим образом:
 ,(2.1.1)
,(2.1.1)
при ограничениях
 (2.1.2)
(2.1.2)
 (2.1.3)
(2.1.3)
В множестве ограничений (2.1.2) и (2.1.3) в зависимости от постановок задач знаки неравенств могут меняться на противоположеные.
В общем случае двухиндексные матрицы – переменных  и
и  и заданная матрица
и заданная матрица  могут быть целочисленными.
могут быть целочисленными.
Рассмотрим задачу при условии, когда переменные  ,
,  и
и  - булевы матрицы. В качестве функции
- булевы матрицы. В качестве функции  часто используют функцию вида
часто используют функцию вида 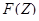 , где
, где
 (2.1.4)
(2.1.4)
Рассмотрим выражение (2.1.4), которое представляет собой произведение матриц переменных  и
и  и заданной матрицы
и заданной матрицы  , на которой определена целевая функция. В отличие от традиционных постановок задач дискретного программирования в данной постановке имеются два типа переменных
, на которой определена целевая функция. В отличие от традиционных постановок задач дискретного программирования в данной постановке имеются два типа переменных  и
и  , переменные
, переменные 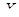 и
и  симметричны относительно заданной матрицы
симметричны относительно заданной матрицы  .
.
В задаче (2.1.1) -(2.1.3) можно выделить множество ограничений вида (2.1.2), которые зависят от переменной  , и множество ограничений вида (2.1.3), которые зависят от переменной
, и множество ограничений вида (2.1.3), которые зависят от переменной  .
.
Функционал вида  можно представить следующим образом:
можно представить следующим образом:
 (2.1.5)
(2.1.5)
 (2.1.6)
(2.1.6)
 (2.1.7)
(2.1.7)
 (2.1.8)
(2.1.8)
 (2.1.9)
(2.1.9)
В постановке задачи (2.1.5) - (2.1.9) выделим блок функции (2.1.6), (2.1.7), зависящий только от переменной  , и блок функций (2.1.8), (2.1.9), зависящий только от переменной
, и блок функций (2.1.8), (2.1.9), зависящий только от переменной  , объединенных единым функционалом вида (2.1.5). Заметим, что в ряде постановок задач может быть блок ограничений вида
, объединенных единым функционалом вида (2.1.5). Заметим, что в ряде постановок задач может быть блок ограничений вида
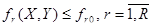 (2.1.10)
(2.1.10)
зависящий от переменных  и
и  .
.
В этом случае можно выделить блок функционала цели вида (2.1.5), (2.1.10).
Отсюда следует.
Определение 2.1. Блочно-симметричной задачей дискретного программирования назовем задачу вида (2.1.5) - (2.1.9), где переменные  и
и  и значения функций
и значения функций  ,
,  ,
,  - целые, либо булевые
- целые, либо булевые
Рассмотрим выражение (2.1.4). из него следует что переменные  и
и  симметричны относительно заданной матрицы
симметричны относительно заданной матрицы  и функция (2.1.4) может быть определена как слева направо, так и наоборот, т.е.
и функция (2.1.4) может быть определена как слева направо, так и наоборот, т.е.
|
|
|
 (2.1.11)
(2.1.11)
На основе общей постановки определим основные свойства сформулированного класса задач, отличающие его от традиционных постановок задач дискретного программирования.
Свойство 1. В блочно-симметричной задаче имеется два типа переменных  и
и  различного содержания, определенных как целочисленные (булевы) матрицы на заданной матрице
различного содержания, определенных как целочисленные (булевы) матрицы на заданной матрице  .
.
В общем случае переменных может быть и больше в зависимости от постановок задач.
Свойство 2. Блочность задачи заключается в выделении в постановке отдельных блоков функций вида (2.1.5), (2.1.10); (2.1.6), (2.1.7) и (2.1.8), (2.1.9), которые соответственно зависят от переменных  и
и  .
.
Как видно из указанных соотношении каждый из блоков имеет свою целевую функцию и координируется общим функционалом вида (2.1.5).
Свойство 3. Блочно-симметричную задачу в большинстве случаев можно представить в матричной форме вида (2.1.11).
Матричная форма постановки блочно-симметричных задач позволяет использовать аппарат теории матриц и разрабатывать эффективные алгоритмы решения задач этого класса.
Свойство 4. Симметричность задачи заключается в возможности вычисления (2.1.11) как слева направо, так и обратном направлении.
Указанные свойства и особенности блочно-симметричных задач ДП позволяют синтезировать алгоритмы, обеспечивающих решение практических задач большой размерности.
В ряде постановок задач функционал (2.1.1) можно представить в виде вектора функций  . В этом случае формулируется многокритериальная блочно-симметричная задача дискретного программирования.
. В этом случае формулируется многокритериальная блочно-симметричная задача дискретного программирования.
Анализ постановки, свойств и особенности блочно-симметричных задач позволил разработать и предложить подход и схему метода решения общей задачи на основе следующего утверждения.
Утверждение. Распределение элементов множества  по непересекающим подмножествам
по непересекающим подмножествам  соответствует логическому сложению строк матриц
соответствует логическому сложению строк матриц  , а распределение элементов множества
, а распределение элементов множества 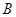 по непересекающимся подмножествам
по непересекающимся подмножествам  - логическому сложению столбцов матрицы
- логическому сложению столбцов матрицы  . [132, 133] Результаты данного утверждения позволяют просто вычислить оценки и направления поиска решения для разработки эффективных алгоритмов.
. [132, 133] Результаты данного утверждения позволяют просто вычислить оценки и направления поиска решения для разработки эффективных алгоритмов.
|
|
|
Введем понятие базиса решения задач. Под базисом понимается заранее заданный состав элементов подмножеств  и
и  .
.
В матрице  базис находится как некоторая матрица
базис находится как некоторая матрица 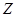 элементы которых определены. Данную матрицу путем перестановки номеров строки столбцов матрицы
элементы которых определены. Данную матрицу путем перестановки номеров строки столбцов матрицы  и их перенумировки всегда можно определить в левом верхнем углу. Такое представление упрощает процедуру оценок и определения направления поиска решения.
и их перенумировки всегда можно определить в левом верхнем углу. Такое представление упрощает процедуру оценок и определения направления поиска решения.
Для решения блочно-симметричной задачи дискретного программирования при условии, когда  ,
,  и
и  - булевы матрицы, разработана и предложена эффективная схема решения задачи. Схема поиска решения состоит из следующих основных этапов:
- булевы матрицы, разработана и предложена эффективная схема решения задачи. Схема поиска решения состоит из следующих основных этапов:
1. В булевой матрице  выделим подматрицу
выделим подматрицу  ,
,  ,
,  и определим её как базис решения задачи.
и определим её как базис решения задачи.
2. Определим матрицу  ,
,  ,
,  направления поиска решения
направления поиска решения  путем логического сложения небазисных строк матрицы
путем логического сложения небазисных строк матрицы  со строками базиса и вычислим значения оценок только по позициям базиса.
со строками базиса и вычислим значения оценок только по позициям базиса.
3. В соответствии с полученными оценками осуществим распределение элементов множества  по множествам
по множествам  . В результате зафиксируем решение
. В результате зафиксируем решение  и промежуточную. Матрицу
и промежуточную. Матрицу  ,
,  ,
,  .
.
4. Определим матрицу  ,
,  ,
,  .
.  направления поиска решения
направления поиска решения  путем логического сложения небазисных столбцов промежуточной матрицы
путем логического сложения небазисных столбцов промежуточной матрицы  со столбцами базиса и вычислим значения оценок только по позициям базиса матрицы
со столбцами базиса и вычислим значения оценок только по позициям базиса матрицы  .
.
5. В соответствии с полученными оценками матрицы  распределим элементы множества
распределим элементы множества 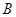 по множествам
по множествам  . В результате фиксируем решение
. В результате фиксируем решение  и целевую матрицу
и целевую матрицу 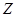 , на которой определено значение целевой функции
, на которой определено значение целевой функции  .
.
6. Следует отметить, что поиск решения задачи может осуществляться как в прямом направлении по схеме  , так и в обратном направлении по схеме
, так и в обратном направлении по схеме  .
.
При заданном базисе решение данного класса задач имеет полиноминальную вычислительную сложность.
|
|
|


