 |
И коэффициента полезного действия трансформатора
|
|
|
|
Приборы и принадлежности: трансформатор школьный, два амперметра
 (1 А) и
(1 А) и  (5 А), два вольтметра
(5 А), два вольтметра  (300 В) и
(300 В) и  (15 В), два ключа, реостат, соединительные провода.
(15 В), два ключа, реостат, соединительные провода.
Цель работы: 1) практическое ознакомление с явлением
электромагнитной индукции;
2) ознакомление с работой трансформатора;
3) определение коэффициента трансформации трансформатора;
4) определение коэффициента полезного действия трансформатора;
Теоретическое введение
В 1831 г. английский физик М. Фарадей открыл, что во всяком замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток индукционным.
Электродвижущая сила индукции  , возникающая в контуре, прямо пропорциональна скорости изменения во времени магнитного потока Ф через поверхность S, ограниченную контуром:
, возникающая в контуре, прямо пропорциональна скорости изменения во времени магнитного потока Ф через поверхность S, ограниченную контуром:

Знак “-” объясняется правилом Э. Ленца. В 1834 г. профессор Петербургской Академии Э. Ленц установил, что: индукционный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного потока, пронизывающего контур.
Частным случаем явления электромагнитной индукции являются явления самоиндукции и взаимной индукции.
Взаимной индукцией называется возбуждение тока в контуре при изменении тока в другом (соседнем) контуре.
Контур, в котором изменяется ток, индуцирует ток не только в других, соседних, контурах, но и в самом себе. Это явление называется самоиндукцией. Электродвижущая сила самоиндукции прямо пропорциональна скорости изменения тока и зависит от индуктивности L контура:
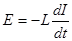
На явлении взаимной индукции и самоиндукции основана работа трансформатора.
|
|
|
Трансформатор представляет собой две индуктивно связанные между собой цепи – две катушки, надетые на один сердечник. Трансформатор был изобретен в 1876 г. П.Н. Яблочковым. Трансформатор позволяет трансформировать, т.е. изменять в определенное число раз, силу тока и напряжение.
 |


~ 
 ~
~ 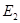
Рис 1
Повышающий трансформатор применяют, например, при передаче электрической энергии на далекие расстояния. На месте потребления напряжение снова понижают.
Принципиальная схема трансформатора показана на рис 1. Первичная 1 и вторичная 2 катушки (обмотки), имеющие соответственно  и
и  витков, надеты на замкнутый сердечник. Если первичную катушку включить в цепь переменного тока, то ток, проходя по ней, создаст переменный магнитный поток, который практически весь сосредоточен внутри сердечника и полностью пронизывает витки первичной и вторичной катушки. Тогда во второй катушке появится э.д.с. взаимной индукции, равная
витков, надеты на замкнутый сердечник. Если первичную катушку включить в цепь переменного тока, то ток, проходя по ней, создаст переменный магнитный поток, который практически весь сосредоточен внутри сердечника и полностью пронизывает витки первичной и вторичной катушки. Тогда во второй катушке появится э.д.с. взаимной индукции, равная 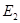 :
:
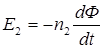 , (1)
, (1)
а в первичной катушке появится э.д.с. самоиндукции  :
:
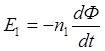 (2)
(2)
Отношение этих э.д.с. равно:
 (3)
(3)
Величина  называется коэффициентом трансформации и показывает во сколько раз э.д.с. во вторичной обмотке больше (или меньше) э.д.с. в первичной обмотке.
называется коэффициентом трансформации и показывает во сколько раз э.д.с. во вторичной обмотке больше (или меньше) э.д.с. в первичной обмотке.
При разомкнутой вторичной обмотке ( ) сила тока в первичной обмотке будет иметь наименьшее значение, поэтому напряжения на зажимах обмоток
) сила тока в первичной обмотке будет иметь наименьшее значение, поэтому напряжения на зажимах обмоток  и
и  мало будут отличаться от э.д.с.
мало будут отличаться от э.д.с.  и
и 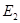 . На этом основании отношение (3) можно записать:
. На этом основании отношение (3) можно записать:
 (4)
(4)
Коэффициентом полезного действия трансформатора называется отношение полезной мощности к потребляемой:

Полезная мощность равна:
 (5)
(5)
Потребляемая мощность:
 (6)
(6)
где  и
и  - углы сдвига фаз между соответствующим током и напряжением. Из-за малости этих углов сдвигом фаз можно пренебречь. Тогда кпд трансформатора определится формулой:
- углы сдвига фаз между соответствующим током и напряжением. Из-за малости этих углов сдвигом фаз можно пренебречь. Тогда кпд трансформатора определится формулой:
 (7)
(7)
Коэффициент полезного действия трансформатора зависит от тока  . С увеличением
. С увеличением  кпд увеличивается. Коэффициент полезного действия трансформатора можно сделать достаточно высоким, если снизить потери, возникающие при передаче энергии из цепи первичной обмотки в цепь вторичной обмотки.
кпд увеличивается. Коэффициент полезного действия трансформатора можно сделать достаточно высоким, если снизить потери, возникающие при передаче энергии из цепи первичной обмотки в цепь вторичной обмотки.
|
|
|
Эти потери связаны с выделением джоулевого тепла в обмотках трансформатора, с затратами на перемагничивание материала сердечника и с нагревом сердечника вихревыми потоками.
В сердечнике трансформатора, находящимся в переменном магнитном поле, возникают вихревые токи. Чтобы уменьшить вихревые токи сердечник изготавливают из отдельных изолированных друг от друга листов. Это увеличивает электрическое сопротивление сердечника, не ухудшая его магнитные свойства. Этот же результат достигается применением ферритов, имеющих высокое удельное сопротивление.
Порядок выполнения работы
1. Собрать цепь согласно схеме (рис 2).
2. Не замыкая ключ 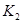 , включить трансформатор в цепь переменного тока (замкнуть ключ
, включить трансформатор в цепь переменного тока (замкнуть ключ  ).
).
3. Записать показания вольтметров  и
и  .
.
4. По формуле (4) рассчитать коэффициент трансформации  .
.
5. Замкнуть ключ 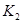 , установить реостатом ток
, установить реостатом ток  .
.
6. Записать показания амперметра 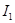 и вольтметра
и вольтметра  в первичной цепи, а также вольтметра
в первичной цепи, а также вольтметра  и амперметра
и амперметра  во вторичной цепи.
во вторичной цепи.
7. По формуле (7) рассчитать кпд.
8. Пункты 5,6,7, повторить для других значений токов  (значения токов
(значения токов  указывает преподаватель).
указывает преподаватель).
9. Данные опытов занести в таблицу.
Таблица
| № | 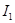 , А , А
|  , В , В
|  , А , А
|  , В , В
| 
| 
|
    1 1
| ||||||
  2 2
| ||||||
  3 3
| ||||||
  4 4
|
Контрольные вопросы
1. В чем заключается явление электромагнитной индукции, самоиндукции, взаимной индукции?
2. Записать и сформулировать уравнение Фарадея.
3. Сформулировать правило Ленца.
4. Устройство и работа трансформатора.
5. Для чего применяется трансформатор?
6. Что называется коэффициентом трансформации и коэффициент полезного действия трансформатора?
7. Можно ли трансформировать постоянный ток?
8. Почему сердечник трансформатора набирают из отдельных листов стали?
 |
~

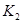
Рис 2.
Литература
1. Курс общей физики А.С. Шубин
|
|
|
2. Курс физики Р.И. Грабовский
ЛАБОРАТОРНАЯ РАБОТА № 2.7
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА 
МЕТОДОМ МАГНЕТРОНА
Приборы и принадлежности: электронная лампа, соленоид, микроамперметр, вольтметр, реостат, источник постоянного тока, УИП-1, ключ.
Цель работы: экспериментально определить удельный заряд электрона.
Теоретическое введение
Удельным зарядом электрона называется отношение заряда электрона  к его массе
к его массе 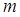 :
:  .
.
В настоящей работе отношение  для электрона определяется при помощи метода, получившего название «метода магнетрона». Это название связано с тем, что применяемая в работе конфигурация электрического и магнитного полей очень напоминает конфигурацию полей в магнетронах – генераторах электромагнитных колебаний в области сверхвысоких частот.
для электрона определяется при помощи метода, получившего название «метода магнетрона». Это название связано с тем, что применяемая в работе конфигурация электрического и магнитного полей очень напоминает конфигурацию полей в магнетронах – генераторах электромагнитных колебаний в области сверхвысоких частот.
В качестве магнетрона можно использовать двухэлектродную электронную лампу с цилиндрическим анодом и катодом, расположенным вдоль оси цилиндрического анода так, что электрическое поле направлено по радиусу.
Движение электронов в этом случае происходит в кольцевом пространстве, заключенном между катодом и анодом двухэлектродной электронной лампы. Лампа помещается внутри соленоида, создающего магнитное поле, параллельное катоду.
Рассмотрим траекторию электронов, движущихся под действием рассматриваемой комбинации электрического и магнитного полей.
Электроны, испускаемые раскаленным катодом, под действием электрического поля между катодом и анодом движутся по радиальным траекториям к аноду при отсутствии магнитного поля ( ).
).
Если по соленоиду пропустить ток, то на движущийся электрон со стороны магнитного поля будет действовать сила Лоренца
 , (1)
, (1)
где  - заряд электрона;
- заряд электрона;
В – индукция магнитного поля;
 - скорость электрона;
- скорость электрона;
 - угол между
- угол между  и
и  .
.
 Так как
Так как 
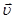
 , а
, а  , формула (1) примет вид:
, формула (1) примет вид:
 (1а)
(1а)
Сила Лоренца всегда направлена перпендикулярно скорости движения заряда и поэтому она работы не совершает. Она изменяет только направление скорости  , а величина скорости и кинетическая энергия заряда при его движении в магнитном поле не изменяются.
, а величина скорости и кинетическая энергия заряда при его движении в магнитном поле не изменяются.
|
|
|
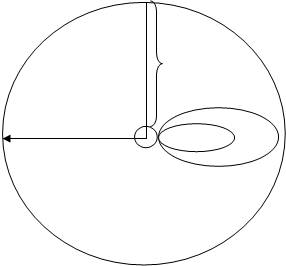 По мере увеличения индукции магнитного поля (усиления силы тока соленоида) траектории электронов будут все более искривляться, а при некотором “критическом” значении индукции магнитного поля электроны перестанут достигать анода и по замкнутым траекториям будут возвращаться обратно на катод (рис 1).
По мере увеличения индукции магнитного поля (усиления силы тока соленоида) траектории электронов будут все более искривляться, а при некотором “критическом” значении индукции магнитного поля электроны перестанут достигать анода и по замкнутым траекториям будут возвращаться обратно на катод (рис 1).
b - 




 |


Рис 1
Под действием силы Лоренца электроны приобретают нормальное ускорение. На основании 2 закона Ньютона можно записать
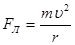 (2)
(2)
Приравнивая правые части уравнений (1а) и (2), получим:
 , (3)
, (3)
где  - масса электрона;
- масса электрона;
 - радиус кривизны траектории электрона в магнитном поле.
- радиус кривизны траектории электрона в магнитном поле.
При критическом значении индукции магнитного поля радиус кривизны траектории электрона равен:
 , (4)
, (4)
где b – радиус цилиндра анода
 - радиус нити катода.
- радиус нити катода.
Так как  << b, то
<< b, то 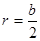 (5)
(5)
Из формулы (3), учитывая равенство (5), найдем удельный заряд  электрона для критического значения индукции
электрона для критического значения индукции 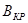 магнитного поля:
магнитного поля:
 =
=  (6)
(6)
При движении электронов в электрическом поле от катода к аноду совершается работа  , где
, где  - разность потенциалов между катодом и анодом. Эта работа равна кинетической энергии электрона:
- разность потенциалов между катодом и анодом. Эта работа равна кинетической энергии электрона:
 (7)
(7)
Отсюда найдем скорость электрона 
Подставив это выражение в формулу (6), найдем:
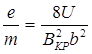 (8)
(8)
Индукция В магнитного поля, создаваемого током соленоида, в СИ определяется по формуле:
 , (9)
, (9)
где  =
= 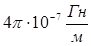 - магнитная постоянная;
- магнитная постоянная;
 = 1 - магнитная проницаемость среды;
= 1 - магнитная проницаемость среды;
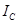 - сила тока, протекающего по соленоиду;
- сила тока, протекающего по соленоиду;
N – число витков соленоида;
 - длина соленоида;
- длина соленоида;
 и
и  - углы, между осью соленоида и радиусом – вектором, проведенном из рассматриваемой точки к концам соленоида.
- углы, между осью соленоида и радиусом – вектором, проведенном из рассматриваемой точки к концам соленоида.



Рис 2
Подставив значение  в формулу (8), получим расчетную формулу для
в формулу (8), получим расчетную формулу для  :
:
 (10)
(10)
Принципиальная схема установки, изображена на рис 3, состоит из трех электрических цепей: анодной цепи, цепи катода и цепи соленоида. Анодная цепь состоит из анода, микроамперметра, потенциометра  , вольтметра, катода и питается от источника постоянного тока.
, вольтметра, катода и питается от источника постоянного тока.
Цепь соленоида состоит из соленоида, миллиамперметра, реостата  , ключа К1
, ключа К1  и питается от источника постоянного тока (0-400 В). Для накала катода лампы подается напряжение 2,15 В от УИП.
и питается от источника постоянного тока (0-400 В). Для накала катода лампы подается напряжение 2,15 В от УИП.
Порядок выполнения работы
1. Собрать электрическую цепь по схеме (рис 3).
2. Цепь соленоида ключом  разомкнуть (
разомкнуть ( ).
).
3. Замкнуть ключом 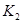 анодную цепь и реостатом
анодную цепь и реостатом  подать на анод лампы напряжение (
подать на анод лампы напряжение ( В).
В).
4. Записать величину анодного тока  .
.
5. Включить с помощью ключа  цепь соленоида.
цепь соленоида.
6. С помощью реостата  увеличивать ток в цепи соленоида от
увеличивать ток в цепи соленоида от  =0 до
=0 до 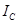 =200 мА через
=200 мА через  =20 мА и записывать в таблицу соответствующие им значения тока
=20 мА и записывать в таблицу соответствующие им значения тока  .
.
|
|
|
7. По полученным данным построить график зависимости 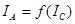 (рис 4), из него найти критическое значение тока (
(рис 4), из него найти критическое значение тока ( ) соленоида.
) соленоида.
8. Измерив длину  соленоида и диаметр его поперечного сечения, найти
соленоида и диаметр его поперечного сечения, найти  и
и  .
.
9. Рассчитать по формуле (10)  . Значения N и b указаны на панели прибора.
. Значения N и b указаны на панели прибора.
10. Повторить опыты для других значений 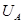 .
.
Контрольные вопросы
1. В чем заключается метод измерения удельного заряда, примененный в данной работе?
2. Объясните устройство и принцип действия магнетрона.
3. Какие силы действуют на заряд в электрическом поле? В магнитном поле?
4. Запишите формулу для силы Лоренца. Укажите, как определить направление ее действия?
5. Выведите формулу (10).
6. Используя табличные данные о заряде и массе электрона, определите значение удельного заряда электрона и, сравнив его с полученным Вами в лабораторной работе, оцените, насколько корректно Вы выполнили лабораторную работу.
Литература
1. Курс общей физики А.С. Шубин
2. Курс физики Р.И. Грабовский


А 

0 – 400 В 6 В
К
 |  |
 2,15 В
2,15 В
Рис 3.



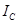
Рис 4
ЛАБОРАТОРНАЯ РАБОТА № 2.8
ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ
НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
Приборы и принадлежности: магнит, компас, секундомер
Теория метода и описание установки
Магнитное поле Земли представляет собою как бы огромный магнит, полюса которого лежат вблизи географических полюсов: вблизи северного географического полюса расположен южный магнитный S, а вблизи южного географического – северный магнитный N (рис. 1)
 |
Рис 1.
Магнитное поле Земли на экваторе направлено горизонтально (точка В), а у магнитных полюсов – вертикально (точка А). В остальных точках земной поверхности магнитное поле Земли направлено под некоторым углом (точка К).
Величину проекции напряженности земного магнитного поля  на горизонтальную плоскость называют горизонтальной составляющей магнитного поля Земли
на горизонтальную плоскость называют горизонтальной составляющей магнитного поля Земли  . Направление этой составляющей принимается за направление магнитного меридиана, а вертикальная плоскость, проходящая через него, называется плоскостью магнитного меридиана. Угол
. Направление этой составляющей принимается за направление магнитного меридиана, а вертикальная плоскость, проходящая через него, называется плоскостью магнитного меридиана. Угол  между направлением магнитного поля Земли и горизонтальной плоскостью называют углом наклонения, а угол
между направлением магнитного поля Земли и горизонтальной плоскостью называют углом наклонения, а угол  между географическим и магнитным меридианами - угол склонения.
между географическим и магнитным меридианами - угол склонения.
Магнитная стрелка, которая может вращаться лишь около вертикальной оси, будет отклоняться в горизонтальной плоскости только под действием горизонтальной составляющей напряженности  магнитного поля Земли.
магнитного поля Земли.
Существуют постоянные магниты, магнитное поле которых создается молекулярными токами. Поле прямолинейного магнита подобно полю соленоида. Как и катушка с током, полосовой магнит характеризуется некоторым магнитным моментом  . Напряженность магнитного поля на достаточно большом расстоянии от системы с магнитным моментом
. Напряженность магнитного поля на достаточно большом расстоянии от системы с магнитным моментом  (контур с током, постоянный магнит) определяется формулой (в системе СИ):
(контур с током, постоянный магнит) определяется формулой (в системе СИ):
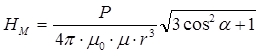 , (1)
, (1)
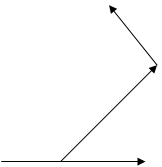 что иллюстрируется рисунком 1
что иллюстрируется рисунком 1 



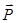
 Рис 1
Рис 1
Возьмем магнит в форме призматического стержня и подвесим его на тонкой и длинной нити так, чтобы он занимал горизонтальное положение (рис 2).
S N Магнит устанавливается в направлении
магнитного меридиана (упругость нити пренебрежимо мала).
Если стержень вывести из положения равновесия (в горизонтальной плоскости), то на него будет действовать вращающий момент М
 , (2)
, (2)
Рис 2 где  - горизонтальная составляющая напряженности магнитного поля Земли, а
- горизонтальная составляющая напряженности магнитного поля Земли, а  - угол отклонения от положения равновесия. Под воздействием механического момента возникают крутильные колебания. Пренебрегая трением и упругостью нити, можно записать уравнение:
- угол отклонения от положения равновесия. Под воздействием механического момента возникают крутильные колебания. Пренебрегая трением и упругостью нити, можно записать уравнение:
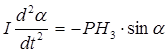
или  ,
,
где I – момент инерции магнита. При малых углах  .
.
Введя подстановку  , получим:
, получим:
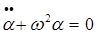 (3)
(3)
Уравнение (3) – это дифференциальное уравнение гармонического колебательного движения. Его решение имеет вид:
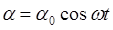 , (4)
, (4)
где  - амплитуда колебаний;
- амплитуда колебаний;
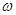 - циклическая частота.
- циклическая частота.
Период колебаний равен:
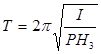 (5)
(5)
Момент инерции призматического магнита относительно оси, проходящей через центр тяжести перпендикулярно к его длине, вычисляется по формуле:
 , (6)
, (6)
где  - длина магнита;
- длина магнита;
 - ширина магнита
- ширина магнита
 - масса магнита.
- масса магнита.
В уравнение (5) входит еще неизвестная величина Р. Рассмотрим второй опыт, который позволит найти связь между  и Р.
и Р.
Возьмем скамью со шкалой и с помощью буссоли, прикрепленной на ее конце, установим ее перпендикулярно магнитному меридиану. После этого возьмем магнит, который должен подвешиваться на нити, и расположим его на скамье так, как показано на рисунке 3.

 Н
Н

N

 S N
S N
Рис 3. S
Стрелка буссоли при этом отклонится на некоторый угол  , отсчитываемый по
, отсчитываемый по
шкале буссоли. Из рисунка видно, что
 , (7)
, (7)
где  - напряженность магнитного поля, создаваемого постоянным магнитом в месте расположения буссоли. Из уравнения (1) найдем
- напряженность магнитного поля, создаваемого постоянным магнитом в месте расположения буссоли. Из уравнения (1) найдем  , принимая
, принимая  и
и  :
:

Отсюда 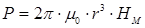 (8)
(8)
Решая совместно уравнения (5), (6), (7) и (8), найдем  :
:
 (9)
(9)
Чтобы исключить ошибку, зависящую от несовпадения магнитной оси буссоли с ее геометрической осью, угол  отсчитывают от обеих концов стрелки. Для исключения ошибки на неточность установления буссоли магнит поворачивают около вертикальной оси на
отсчитывают от обеих концов стрелки. Для исключения ошибки на неточность установления буссоли магнит поворачивают около вертикальной оси на 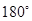 и повторяют измерения угла
и повторяют измерения угла  . Из четырех полученных значений находят среднее, которым пользуются в дальнейших вычислениях.
. Из четырех полученных значений находят среднее, которым пользуются в дальнейших вычислениях.
|
|
|


