 |
Длинна дуги кривой заданной в явном виде.
|
|
|
|
БИНОМИАЛЬНЫМ ДИФФЕРЕНЦИАЛОМ НАЗЫВАЕТСЯ ВЫРАЖЕНИЕ ВИДА
 , "a,bÎR, m,n,p Î Q.
, "a,bÎR, m,n,p Î Q.
I. р – целое, р  0.
0.
р<0, p Î -N, нужно делать замену переменной t=  , где S=НОК(m,n).
, где S=НОК(m,n).
II. p – дробное, но 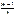 – целое. Пусть р = r/s, t=
– целое. Пусть р = r/s, t= 
III. p – дробное,  – дробное,
– дробное, 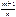 +р – целое,
+р – целое,
p= r/s, t=  =
=  .
.
Определённый интеграл. Задачи, приводящие к понятию определённого интеграла. Определение определённого интеграла.
Задача о площади криволинейной трапеции: Рассмотрим плоскую фигуру ограниченную y=f(x), разобьём её точками a=x0<x1<…<xn=b,  . В каждом из частичных сегментов выберем точку «кси итая».
. В каждом из частичных сегментов выберем точку «кси итая».
 . Обозначим через
. Обозначим через  если существует конечный предел интегральной суммы
если существует конечный предел интегральной суммы  при лямбда
при лямбда  , то этот предел – площадь криволинейной трапеции.
, то этот предел – площадь криволинейной трапеции.
Опр.: Пусть дана ф-я f(x) на [a,b]. Разобьём отрезок точками a=x0<x1<…<xn=b,  . В каждом из частичных сегментов выберем точку «кси итая». Обозначим через
. В каждом из частичных сегментов выберем точку «кси итая». Обозначим через  . Если существует конечный предел
. Если существует конечный предел  , то он наз определённым интегралом от f(x).
, то он наз определённым интегралом от f(x).
Условия существования определённого интеграла. Свойства определённого интеграла.
Теор.: (необходимое условие существования определённого интеграла) для того чтобы существовал определённый интеграл необходимо чтобы ф-я была непрерывна на интервале интегрирования.
Док-во: (метод от противного) пусть ф-я интегрируемая но не ограниченная на [a,b]….
Теор.: (дост. условие существования определённого интеграла) Если ф-я непрерывна на [a,b], то она интегрируема на нем.
Свойства определенного интеграла.
1) 
2) 
3) 
4) Если f(x) £ j(x) на отрезке [a, b] a < b, то 
5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что
|
|
|

7) Для произвольных чисел a, b, c справедливо равенство:

8) 
Вычисление определённого интеграла с помощью формулы Ньютона-Лейбница. Замена переменной и интегрирование по частям в определённом интеграле.
Теорема: (Теорема Ньютона – Лейбница)Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то  .
.
Замена переменных.
Пусть задан интеграл  , где f(x) – непрерывная функция на отрезке [a, b].
, где f(x) – непрерывная функция на отрезке [a, b].
Введем новую переменную в соответствии с формулой x = j(t).
Тогда если
1) j(a) = а, j(b) = b
2) j(t) и j¢(t) непрерывны на отрезке [a, b]
3) f(j(t)) определена на отрезке [a, b], то  , тогда
, тогда 
Интегрирование по частям.
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям: 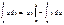
Вычисление площадей с помощью определённого интеграла. Вычисление площадей в параметрической форме.
Пусть кривая задана параметрически, тогда 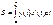 .
.
Вычисление площади фигуры в полярных координатах.
Пусть дан сектор АВО, ограниченный кривой АВ и двумя радиус векторами.  >0 и непрерывная на
>0 и непрерывная на  . Разобьем сектор на n произвольных частей углами
. Разобьем сектор на n произвольных частей углами  . Выберем в каждом сегменте точку «кси итая» r=r(«кси итая»). S=0.5*R2*l. Значит площадь сегмента =
. Выберем в каждом сегменте точку «кси итая» r=r(«кси итая»). S=0.5*R2*l. Значит площадь сегмента = 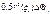 . Площадь всего сектора это сумма этих площадей. Тогда переходим к интегралу:
. Площадь всего сектора это сумма этих площадей. Тогда переходим к интегралу:  .
.
Объём цилиндра. Объём тела по площадям параллельных сечений.
Пусть имеется тело ограниченное сверху и снизу некоторой квадрируемой областью с высотой H, тогда V=Sоснов*H.
Пусть тело ограничено некоторой замкнутой поверхностью. Примем какую-нибудь прямую за ось ОХ. И пересечём тело плоскостями перпендикулярными оси ОХ. Тогда в сечении получатся плоские фигуры, площади которых зависят от Х. Разобьем отрезок [a,b] на n произвольных частей точками 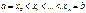 . Через каждую точку проведём сечение параллельное некоторой плоскости P. В каждом частичном сегменте возьмём некоторую точку «кси итая». S(«кси итая»)-площадь,
. Через каждую точку проведём сечение параллельное некоторой плоскости P. В каждом частичном сегменте возьмём некоторую точку «кси итая». S(«кси итая»)-площадь,  , тогда
, тогда  .
.  , далее объём равен пределу и далее интегралу
, далее объём равен пределу и далее интегралу  .
.
|
|
|
Объём тела вращения
Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса  , то объем тела вращения может быть легко найден по полученной выше формуле:
, то объем тела вращения может быть легко найден по полученной выше формуле:

Длина дуги кривой.
Длина ломаной линии, которая соответствует дуге, может быть найдена как  .
.
Тогда длина дуги равна  .
.
Из геометрических соображений: 
В то же время 
Тогда можно показать что  Т.е.
Т.е. 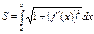
Длинна дуги кривой заданной в явном виде.
Теор.: Пусть кривая АВ задана вуравнением y=f(x), где f(x) и f’(x) – непрерывные на отрезке [a,b] функции, тогда длинна дуги:  (для доказательства нужно разбить кривую точками).
(для доказательства нужно разбить кривую точками).
|
|
|


