Главная | Обратная связь | Поможем написать вашу работу!

Алгоритм Флойда – Уоршелла

Двоичное дерево поиска

Двоичное дерево поиска представляет собой бинарное дерево, обладающее следующим свойством. Значение любого из узлов L₁, L₂, L₃, …, L_n левого поддерева, выходящего из некоторого корня K, всегда меньше значения самого этого корня: Value(L_i) < Value(K), тогда как отношение узлов R₁, R₂, R₃, …, R_n правого поддерева к корню определяется нестрогим неравенством: Value(R_i) >= Value(K). Ниже изображен пример двоичного дерева поиска.

Здесь из корня, значение которого 10, выходят два поддерева, причем все левые элементы меньше правых и самого корня, а правые, соответственно, больше. Такое следование продолжается и на следующих уровнях.

Алгоритм поиска по такой конструкции будет достаточно эффективен, ведь максимальное количество шагов, которое может понадобиться для обнаружения нужного элемента, равно количеству уровней самого бинарного дерева поиска. Поиск элемента в двоичном дереве состоит из следующих шагов:

· если дерево не содержит в себе элементов, то остановить поиск

· иначе сравнить искомый элемент (ключ) с корнем:

o если значение ключа равно значению корня – поиск завершен, иначе

o если значение ключа больше значения корня – искать в правой части, иначе

o если значение ключа меньше значения корня – искать в левой части.

Эти действия выполняются до того момента, когда элемент будет найден, либо окажется что он вовсе отсутствует.

Рассмотренный метод для изображенного на рисунке выше бинарного дерева поиска, будет работать по такому сценарию. Допустим, значение ключа равно 13, и нужно найти узел с тем же значением. Вначале сравнивается ключ с корнем, значение которого 10. Так как 13 больше 10, поэтому далее для поиска следует выбрать правую ветку дерева, ведь элементы в ней больше 10, что известно из основного свойства бинарного дерева поиска. Далее поиск как бы переходит на новое дерево, которое является поддеревом изначального дерева. Тут ключ 13 сравнивается с узлом 16. Первое значение меньше, следовательно, поиск продолжается в левой части, и именно там расположен искомый элемент.

Помимо операции поиска, на двоичном дереве поиска эффективно применять операции добавления и удаления элемента. К тому же во многих ситуациях целесообразным оказывается обычное двоичное дерево переделать в дерево поиска, отсортировав его элементы одним из алгоритмов сортировки.

Двоичное дерево поиска

· если дерево не содержит в себе элементов, то остановить поиск

· иначе сравнить искомый элемент (ключ) с корнем:

o если значение ключа равно значению корня – поиск завершен, иначе

o если значение ключа больше значения корня – искать в правой части, иначе

o если значение ключа меньше значения корня – искать в левой части.

Эти действия выполняются до того момента, когда элемент будет найден, либо окажется что он вовсе отсутствует.

Двоичное дерево поиска

· если дерево не содержит в себе элементов, то остановить поиск

· иначе сравнить искомый элемент (ключ) с корнем:

o если значение ключа равно значению корня – поиск завершен, иначе

o если значение ключа больше значения корня – искать в правой части, иначе

o если значение ключа меньше значения корня – искать в левой части.

Эти действия выполняются до того момента, когда элемент будет найден, либо окажется что он вовсе отсутствует.

Поиск в ширину

Поиск в ширину (обход по уровням) – один из алгоритмов обхода графа. Метод лежит в основе некоторых других алгоритмов близкой тематики. Поиск в ширину подразумевает поуровневое исследование графа: вначале посещается корень – произвольно выбранный узел, затем – все потомки данного узла, после этого посещаются потомки потомков и т.д. Вершины просматриваются в порядке возрастания их расстояния от корня.

Пусть задан граф G=(V, E) и корень s, с которого начинается обход. После посещения узла s, следующими за ним будут посещены смежные с s узлы (множество смежных с s узлов обозначим как q; очевидно, что q⊆V, то есть q – некоторое подмножество V). Далее, эта процедура повториться для вершин смежных с вершинами из множества q, за исключением вершины s, т. к. она уже была посещена. Так, продолжая обходить уровень за уровнем, алгоритм обойдет все доступные из s вершины множества V. Алгоритм прекращает свою работу после обхода всех вершин графа, либо в случае выполнения наличествующего условия.

Рассматривая следующий пример, будем считать, что в процессе работы алгоритма каждая из вершин графа может быть окрашена в один из трех цветов: черный, белый или серый. Изначально все вершины белые. В процессе обхода каждая из вершин, по мере обнаружения, окрашивается сначала в серый, а затем в черный цвет. Определенный момент обхода описывает следующие условие: если вершина черная, то все ее потомки окрашены в серый или черный цвет.

Имеем смешанный граф (см. рис.) с |V| = 4 и |E| = 5. Выполним обход его вершин, используя алгоритм поиска в ширину. В качестве стартовой вершины возьмем узел 3. Сначала он помечается серым как обнаруженный, а затем черным, поскольку обнаружены смежные с ним узлы (1 и 4), которые, в свою очередь, в указанном порядке помечаются серым. Следующим в черный окрашивается узел 1, и находятся его соседи – узел 2, который становится серым. И, наконец, узлы 4 и 2, в данном порядке, просматриваются, обход в ширину завершается.

Алгоритм поиска в ширину работает как на ориентированных, так и на неориентированных графах. Дать понять это был призван смешанный граф, используемый в примере. Стоит отметить, в неориентированном связном графе данный метод обойдет все имеющиеся узлы, а в смешанном или орграфе это необязательно произойдет. К тому же, до сих пор рассматривался обход всех вершин, но вполне вероятно, достаточным окажется, например просмотр определенного их количества, либо нахождение конкретной вершины. В таком случае придется немного приспособить алгоритм, а не изменять его полностью или вовсе отказаться от использования такового.

Теперь перейдем к более формальному описанию алгоритма поиска в ширину. Основными объектами – тремя структурами данных, задействованными в программе, будут:

· матрица смежности графа GM;

· очередь queue;

· массив посещенных вершин visited.

Две первые структуры имеют целочисленный тип данных, последняя – логический. Посещенные вершины, заносятся в массив visited, что предотвратит зацикливание, а очередь queue будет хранить задействованные узлы. Напомним, что структура данных «очередь» работает по принципу «первый пришел – первый вышел». Рассмотрим разбитый на этапы процесс обхода графа:

1. массив visited обнуляется, т. е. ни одна вершина графа еще не была посещена;

2. в качестве стартовой, выбирается некоторая вершина s и помещается в очередь (в массив queue);

3. вершина s исследуется (помечается как посещенная), и все смежные с ней вершины помещаются в конец очереди, а сама она удаляется;

4. если на данном этапе очередь оказывается пустой, то алгоритм прекращает свою работу; иначе посещается вершина, стоящая в начале очереди, помечается как посещенная, и все ее потомки заносятся в конец очереди;

5. пункт 4 выполняется пока это возможно.

Поиск в ширину, начиная со стартовой вершины, постепенно уходит от нее все дальше и дальше, проходя уровень за уровнем. Получается, что по окончанию работы алгоритма будут найдены все кратчайшие пути из начальной вершины до каждого доступного из нее узла.

Для реализации алгоритма на ЯП потребуется: умение программно задавать граф, а также иметь представление о такой структуре данных, как очередь.

Код программы на C++:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

#include "stdafx.h"#include <iostream> using namespace std; const int n=4; int i, j; //матрица смежности графа int GM[n][n] = { {0, 1, 1, 0}, {0, 0, 1, 1}, {1, 0, 0, 1}, {0, 1, 0, 0} }; //поиск в ширину void BFS(bool *visited, int unit) { int *queue=new int[n]; int count, head; for (i=0; i<n; i++) queue[i]=0; count=0; head=0; queue[count++]=unit; visited[unit]=true; while (head<count) { unit=queue[head++]; cout<<unit+1<<" "; for (i=0; i<n; i++) if (GM[unit][i] &&!visited[i]) { queue[count++]=i; visited[i]=true; } } delete []queue; } //главная функция void main() { setlocale(LC_ALL, "Rus"); int start; cout<<"Стартовая вершина >> "; cin>>start; bool *visited=new bool[n]; cout<<"Матрица смежности графа: "<<endl; for (i=0; i<n; i++) { visited[i]=false; for (j=0; j<n; j++) cout<<" "<<GM[i][j]; cout<<endl; } cout<<"Порядок обхода: "; BFS(visited, start-1); delete []visited; system("pause>>void"); }

В двух этих программах используется граф, изображенный на предыдущем рисунке, точнее его матрица смежности. На ввод может поддаваться только одно из 4 значений, т. к. в качестве стартовой возможно указать лишь одну из 4 имеющихся вершин (программы не предусматривают некорректных входных данных):

Входные данные	Выходные данные
	1 2 3 4
	2 3 4 1
	3 1 4 2
	4 2 3 1

Граф представлен матрицей смежности, и относительно эффективности это не самый лучший вариант, так как время, затраченное на ее обход, оценивается в O(|V|²), а сократить его можно до O(|V|+|E|), используя список смежности.

Поиск в глубину

Поиск в глубину (англ. depth-first search, DFS) – это рекурсивный алгоритм обхода вершин графа. Если метод поиска в ширину производился симметрично (вершины графа просматривались по уровням), то данный метод предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность дальнейшего продвижения, означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина). Отсутствие последнего свидетельствует об одной из двух возможных ситуаций: либо все вершины графа уже просмотрены, либо просмотрены все те, что доступны из вершины, взятой в качестве начальной, но не все (несвязные и ориентированные графы допускают последний вариант).

Рассмотрим то, как будет вести себя алгоритм на конкретном примере. Приведенный далее неориентированный связный граф имеет в сумме 5 вершин. Сначала необходимо выбрать начальную вершину. Какая бы вершина в качестве таковой не была выбрана, граф в любом случае исследуется полностью, поскольку, как уже было сказано, это связный граф без единого направленного ребра.
Пусть обход начнется с узла 1, тогда порядок последовательности просмотренных узлов будет следующим: 1 2 3 5 4. Если выполнение начать, например, с узла 3, то порядок обхода окажется иным: 3 2 1 5 4.

Алгоритм поиска в глубину базируется на рекурсии, т. е. функция обхода, по мере выполнения, вызывает сама себя, что делает код в целом довольно компактным. Псевдокод алгоритма:

Заголовок функции DFS(st)
Вывести (st)
visited[st] ← посещена;
Для r=1 до n выполнять
Если (graph[st, r] ≠ 0) и (visited[r] не посещена) то DFS(r)

Здесь DFS (depth-firstsearch) – название функции. Единственный ее параметр st – стартовый узел, передаваемый из главной части программы как аргумент. Каждому из элементов логического массива visited заранее присваивается значение false, т. е. каждая из вершин изначально будет значиться как не посещенная. Двумерный массив graph – это матрица смежности графа. Большую часть внимания следует сконцентрировать на последней строке. Если элемент матрицы смежности, на каком то шаге равен 1 (а не 0) и вершина с тем же номером, что и проверяемый столбец матрицы при этом не была посещена, то функция рекурсивно повторяется. В противном случае функция возвращается на предыдущую стадию рекурсии.

Код программы на C++:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

#include "stdafx.h"#include <iostream> using namespace std; const int n=5; int i, j; bool *visited=new bool[n]; //матрица смежности графа int graph[n][n] = { {0, 1, 0, 0, 1}, {1, 0, 1, 1, 0}, {0, 1, 0, 0, 1}, {0, 1, 0, 0, 1}, {1, 0, 1, 1, 0} }; //поиск в глубину void DFS(int st) { int r; cout<<st+1<<" "; visited[st]=true; for (r=0; r<=n; r++) if ((graph[st][r]!=0) && (!visited[r])) DFS(r); } //главная функция void main() { setlocale(LC_ALL, "Rus"); int start; cout<<"Матрица смежности графа: "<<endl; for (i=0; i<n; i++) { visited[i]=false; for (j=0; j<n; j++) cout<<" "<<graph[i][j]; cout<<endl; } cout<<"Стартовая вершина >> "; cin>>start; //массив посещенных вершин bool *vis=new bool[n]; cout<<"Порядок обхода: "; DFS(start-1); delete []visited; system("pause>>void"); }

Для простоты понимания результата, выдаваемого двумя программами, взят неориентированный граф, приводимый ранее в качестве примера, и представленный матрицей смежности graph

Алгоритм Беллмана — Форда

История алгоритма связана сразу с тремя независимыми математиками: Лестером Фордом, Ричардом Беллманом и Эдвардом Муром. Форд и Беллман опубликовали алгоритм в 1956 и 1958 годах соответственно, а Мур сделал это в 1957 году. И иногда его называют алгоритмом Беллмана – Форда – Мура. Метод используется в некоторых протоколах дистанционно-векторной маршрутизации, например в RIP (Routing Information Protocol – Протокол маршрутной информации).

Также как и алгоритм Дейкстры, алгоритм Беллмана — Форда вычисляет во взвешенном графе кратчайшие пути от одной вершины до всех остальных. Он подходит для работы с графами, имеющими ребра с отрицательным весом. Но спектр применимости алгоритма затрагивает не все такие графы, ввиду того, что каждый очередной проход по пути, составленному из ребер, сумма весов которых отрицательна (т. е. по отрицательному циклу), лишь улучшает требуемое значение. Бесконечное число улучшений делает невозможным определение одного конкретного значения, являющегося оптимальным. В связи с этим алгоритм Беллмана — Форда не применим к графам, имеющим отрицательные циклы, но он позволяет определить наличие таковых, о чем будет сказано позже.

Решить задачу, т. е. найти все кратчайшие пути из вершины s до всех остальных, используя алгоритм Беллмана — Форда, это значит воспользоваться методом динамического программирования: разбить ее на типовые подзадачи, найти решение последним, покончив тем самым с основной задачей. Здесь решением каждой из таких подзадач является определение наилучшего пути от одного отдельно взятого ребра, до какого-либо другого. Для хранения результатов работы алгоритма заведем одномерный массив d[]. В каждом его i-ом элементе будет храниться значение кратчайшего пути из вершины s до вершины i (если таковое имеется). Изначально, присвоим элементам массива d[] значения равные условной бесконечности (например, число заведомо большее суммы всех весов), а в элемент d[s] запишем нуль. Так мы задействовали известную и необходимую информацию, а именно известно, что наилучший путь из вершины s в нее же саму равен 0, и необходимо предположить недоступность других вершин из s. По мере выполнения алгоритма, для некоторых из них, это условие окажется ложным, и вычисляться оптимальные стоимости путей до этих вершин из s.

Задан граф G=(V, E), n=|V|, а m=|E|. Обозначим смежные вершины этого графа символами v и u (vÎV и uÎV), а вес ребра (v, u) символом w. Иначе говоря, вес ребра, выходящего из вершины v и входящего в вершину u, будет равен w. Тогда ключевая часть алгоритма Беллмана — Форда примет следующий вид:

Для i от 1 до n-1 выполнять
Для j от 1 до m выполнять
Если d[v] + w(v, u) < d[u] то
d[u] < d[v] + w(v, u)

На каждом n-ом шаге осуществляются попытки улучшить значения элементов массива d[]: если сумма, составленная из веса ребра w(v, u) и веса хранящегося в элементе d[v], меньше веса d[u], то она присваивается последнему.

Код программы на C++:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

#include "stdafx.h"#include <iostream>#define inf 100000 using namespace std; struct Edges{ int u, v, w; }; const int Vmax=1000; const int Emax=Vmax*(Vmax-1)/2; int i, j, n, e, start; Edges edge[Emax]; int d[Vmax]; //алгоритм Беллмана-Форда void bellman_ford(int n, int s) { int i, j; for (i=0; i<n; i++) d[i]=inf; d[s]=0; for (i=0; i<n-1; i++) for (j=0; j<e; j++) if (d[edge[j].v]+edge[j].w<d[edge[j].u]) d[edge[j].u]=d[edge[j].v]+edge[j].w; for (i=0; i<n; i++) if (d[i]==inf) cout<<endl<<start<<"->"<<i+1<<"="<<"Not"; else cout<<endl<<start<<"->"<<i+1<<"="<<d[i]; } //главная функция void main() { setlocale(LC_ALL, "Rus"); int w; cout<<"Количество вершин > "; cin>>n; e=0; for (i=0; i<n; i++) for (j=0; j<n; j++) { cout<<"Вес "<<i+1<<"->"<<j+1<<" > "; cin>>w; if (w!=0) { edge[e].v=i; edge[e].u=j; edge[e].w=w; e++; } } cout<<"Стартовая вершина > "; cin>>start; cout<<"Список кратчайших путей:"; bellman_ford(n, start-1); system("pause>>void"); }

Здесь граф представлен упрощенным списком ребер, который формируется по мере ввода пользователем матрицы весов. Основная часть алгоритма Беллмана – Форда (проверка условия) выполняется m*(n-1) раз, т. к. число повторений внешнего цикла равно n-1, а внутреннего – m. Отказ от n-ой итерации целесообразен, поскольку алгоритм справляется со своей задачей за n-1 шаг, но запуск внешнего цикла n раз позволит выявить наличие отрицательного цикла в графе. Проверить это можно, например, при помощи следующей модификации:

1 2 3 4 5 6 7 8 9 10 11 12

bool x=true; for (i=0; i<n; i++) { if (i!=n-1) for (j=0; j<e; j++) if (d[edge[j].v]+edge[j].w<d[edge[j].u]) d[edge[j].u]=d[edge[j].v]+edge[j].w; if (i==n-1) for (j=0; j<e; j++) if (d[edge[j].v]+edge[j].w<d[edge[j].u]) x=false; } if (!x) cout<<endl<<"Граф содержит отриц. циклы"<<endl;

Здесь внешний цикл выполняется n раз (в C++ принято начальным указывать значение 0, поэтому для данного кода n-1 раз), и если на n-ой стадии будет возможно улучшение, то это свидетельствует о наличие отрицательного цикла.

Алгоритм Дейкстры

Алгоритм голландского ученого Эдсгера Дейкстры находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных. С его помощью, при наличии всей необходимой информации, можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города до каждого из многих других, или в какие страны выгодней экспортировать нефть и тому подобное. Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом, т. е. если, например, некоторая система предусматривает убыточные для Вашей фирмы маршруты, то для работы с ней следует воспользоваться отличным от алгоритма Дейкстры методом.

Для программной реализации алгоритма понадобиться два массива: логический visited – для хранения информации о посещенных вершинах и численный distance, в который будут заноситься найденные кратчайшие пути. Итак, имеется граф G=(V, E). Каждая из вершин входящих во множество V, изначально отмечена как не посещенная, т. е. элементам массива visited присвоено значение false. Поскольку самые выгодные пути только предстоит найти, в каждый элемент вектора distance записывается такое число, которое заведомо больше любого потенциального пути (обычно это число называют бесконечностью, но в программе используют, например максимальное значение конкретного типа данных). В качестве исходного пункта выбирается вершина s и ей приписывается нулевой путь: distance[s]=0, т. к. нет ребра из s в s (метод не предусматривает петель). Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть таковыми будут t и u] и поочередно исследуются, а именно вычисляется стоимость маршрута из s поочередно в каждую из них:

· distance[t]=distance[s]+весинцидентного s и t ребра;

· distance[u]=distance[s]+ весинцидентного s и u ребра.

Но вполне вероятно, что в ту или иную вершину из s существует несколько путей, поэтому цену пути в такую вершину в массиве distance придется пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а наименьшее ставиться в соответствие вершине.

После обработки смежных с s вершин она помечается как посещенная: visited[s]=true, и активной становится та вершина, путь из s в которую минимален. Допустим, путь из s в u короче, чем из s в t, следовательно, вершина u становиться активной и выше описанным образом исследуются ее соседи, за исключением вершины s. Далее, u помечается как пройденная: visited[u]=true, активной становится вершина t, и вся процедура повторяется для нее. Алгоритм Дейкстры продолжается до тех пор, пока все доступные из s вершины не будут исследованы.

Теперь на конкретном графе проследим работу алгоритма, найдем все кратчайшие пути между истоковой и всеми остальными вершинами. Размер (количество ребер) изображенного ниже графа равен 7 (|E|=7), а порядок (количество вершин) – 6 (|V|=6). Это взвешенный граф, каждому из его ребер поставлено в соответствие некоторое числовое значение, поэтому ценность маршрута необязательно определяется числом ребер, лежащих между парой вершин.

Из всех вершин входящих во множество V выберем одну, ту, от которой необходимо найти кратчайшие пути до остальных доступных вершин. Пусть таковой будет вершина 1. Длина пути до всех вершин, кроме первой, изначально равна бесконечности, а до нее – 0, т. к. граф не имеет петель.

У вершины 1 ровно 3 соседа (вершины 2, 3, 5), и чтобы вычислить длину пути до них нужно сложить вес дуг, лежащих между вершинами: 1 и 2, 1 и 3, 1 и 5 со значением первой вершины (с нулем):

· 2←1+0

· 3←4+0

· 5←2+0

Как уже отмечалось, получившиеся значения присваиваются вершинам, лишь в том случае если они «лучше» (меньше) тех которые значатся на настоящий момент. А так как каждое из трех чисел меньше бесконечности, они становятся новыми величинами, определяющими длину пути из вершины 1 до вершин 2, 3 и 5.

Далее, активная вершина помечается как посещенная, статус «активной» (красный круг) переходит к одной из ее соседок, а именно к вершине 2, поскольку она ближайшая к ранее активной вершине.

У вершины 2 всего один не рассмотренный сосед (вершина 1 помечена как посещенная), расстояние до которого из нее равно 9, но нам необходимо вычислить длину пути из истоковой вершины, для чего нужно сложить величину приписанную вершине 2 с весом дуги из нее в вершину 4:

· 4←1+9

Условие «краткости» (10<∞) выполняется, следовательно, вершина 4 получает новое значение длины пути.

Вершина 2 перестает быть активной, также как и вершина 1 удаляется из списка не посещённых. Теперь тем же способом исследуются соседи вершины 5, и вычисляется расстояние до них.

Когда дело доходит до осмотра соседей вершины 3, то тут важно не ошибиться, т. к. вершина 4 уже была исследована и расстояние одного из возможных путей из истока до нее вычислено. Если двигаться в нее через вершину 3, то путь составит 4+7=11, а 11>10, поэтому новое значение игнорируется, старое остается.

Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5. Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими. Так, например, будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и всеми остальными вершинами, рассматриваемого графа:

1→1=0
1→2=1
1→3=4
1→4=10
1→5=2
1→6=10

В программе, находящей ближайшие пути между вершинами посредством метода Дейкстры, граф будет представлен в виде не бинарной матрицы смежности. Вместо единиц в ней будут выставлены веса ребер, функция нулей останется прежней: показывать, между какими вершинами нет ребер или же они есть, но отрицательно направленны.

Код программы на C++:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

#include "stdafx.h"#include <iostream> using namespace std; const int V=6; //алгоритм Дейкстры void Dijkstra(int GR[V][V], int st) { int distance[V], count, index, i, u, m=st+1; bool visited[V]; for (i=0; i<V; i++) { distance[i]=INT_MAX; visited[i]=false; } distance[st]=0; for (count=0; count<V-1; count++) { int min=INT_MAX; for (i=0; i<V; i++) if (!visited[i] && distance[i]<=min) { min=distance[i]; index=i; } u=index; visited[u]=true; for (i=0; i<V; i++) if (!visited[i] && GR[u][i] && distance[u]!=INT_MAX && distance[u]+GR[u][i]<distance[i]) distance[i]=distance[u]+GR[u][i]; } cout<<"Стоимость пути из начальной вершины до остальных:\t\n"; for (i=0; i<V; i++) if (distance[i]!=INT_MAX) cout<<m<<" > "<<i+1<<" = "<<distance[i]<<endl; else cout<<m<<" > "<<i+1<<" = "<<"маршрут недоступен"<<endl; } //главная функция void main() { setlocale(LC_ALL, "Rus"); int start, GR[V][V]={ {0, 1, 4, 0, 2, 0}, {0, 0, 0, 9, 0, 0}, {4, 0, 0, 7, 0, 0}, {0, 9, 7, 0, 0, 2}, {0, 0, 0, 0, 0, 8}, {0, 0, 0, 0, 0, 0}}; cout<<"Начальная вершина >> "; cin>>start; Dijkstra(GR, start-1); system("pause>>void"); }

Алгоритм Флойда – Уоршелла

Наиболее часто используемое название, метод получил в честь двух американских исследователей Роберта Флойда и Стивена Уоршелла, одновременно открывших его в 1962 году. Реже встречаются другие варианты наименований: алгоритм Рой – Уоршелла или алгоритм Рой – Флойда. Рой – фамилия профессора, который разработал аналогичный алгоритм на 3 года раньше коллег (в 1959 г.), но это его открытие осталось безвестным. Алгоритм Флойда – Уоршелла – динамический алгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных.

Для реализации алгоритма Флойда – Уоршелла сформируем матрицу смежности D[][] графа G=(V, E), в котором каждая вершина пронумерована от 1 до |V|. Эта матрица имеет размер |V|´|V|, и каждому ее элементу D[i][j] присвоен вес ребра, идущего из вершины i в вершину j. По мере выполнения алгоритма, данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины i в вершину j (отказ от выделения специального массива для этой цели сохранит память и время). Теперь, перед составлением основной части алгоритма, необходимо разобраться с содержанием матрицы кратчайших путей. Поскольку каждый ее элемент D[i][j] должен содержать наименьший из имеющихся маршрутов, то сразу можно сказать, что для единичной вершины он равен нулю, даже если она имеет петлю (отрицательные циклы не рассматриваются), следовательно, все элементы главной диагонали (D[i][i]) нужно обнулить. А чтобы нулевые недиагональные элементы (матрица смежности могла иметь нули в тех местах, где нет непосредственного ребра между вершинами i и j) сменили по возможности свое значение, определим их равными бесконечности, которая в программе может являться, например, максимально возможной длинной пути в графе, либо просто – большим числом.Ключевая часть алгоритма, состоя из трех циклов, выражения и условного оператора, записывается довольно компактно:

Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если D[i][k]+D[k][j]<D[i][j] то D[i][j] ←D[i][k]+D[k][j]

Кратчайший путь из вершины i в вершину j может проходить, как только через них самих, так и через множество других вершин k∈(1, …, |V|). Оптимальным из i в j будет путь или не проходящий через k, или проходящий. Заключить о наличии второго случая, значит установить, что такой путь идет из i до k, а затем из k до j, поэтому должно заменить, значение кратчайшего пути D[i][j] суммой D[i][k]+D[k][j].Рассмотрим полный код алгоритма Флойда – Уоршелла на C++ и Паскале, а затем детально разберем последовательность выполняемых им действий.

Код программы на C++:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

#include "stdafx.h"#include <iostream> using namespace std; const int maxV=1000; int i, j, n; int GR[maxV][maxV]; //алгоритм Флойда-Уоршелла void FU(int D[][maxV], int V) { int k; for (i=0; i<V; i++) D[i][i]=0; for (k=0; k<V; k++) for (i=0; i<V; i++) for (j=0; j<V; j++) if (D[i][k] && D[k][j] && i!=j) if (D[i][k]+D[k][j]<D[i][j] || D[i][j]==0) D[i][j]=D[i][k]+D[k][j]; for (i=0; i<V; i++) { for (j=0; j<V; j++) cout<<D[i][j]<<"\t"; cout<<endl; } } //главная функция void main() { setlocale(LC_ALL, "Rus"); cout<<"Количество вершин в графе > "; cin>>n; cout<<"Введите матрицу весов ребер:\n"; for (i=0; i<n; i++) for (j=0; j<n; j++) { cout<<"GR["<<i+1<<"]["<<j+1<<"] > "; cin>>GR[i][j]; } cout<<"Матрица кратчайших путей:"<<endl; FU(GR, n); system("pause>>void"); }

Положим, что в качестве матрицы смежности, каждый элемент которой хранит вес некоторого ребра, была задана следующая матрица:

Количество вершин в графе, представлением которого является данная матрица, равно 3, и, причем между каждыми двумя вершинами существует ребро. Вот собственно сам этот граф:

Задача алгоритма: перезаписать данную матрицу так, чтобы каждая ячейка вместо веса ребра из i в j, содержала кратчайший путь из i в j. Для примера взят совсем маленький граф, и поэтому не будет не чего удивительного, если матрица сохранит свое изначальное состояние. Но результат тестирования программы показывает замену двух значений в ней. Следующая схема поможет с анализом этого конкретного примера.

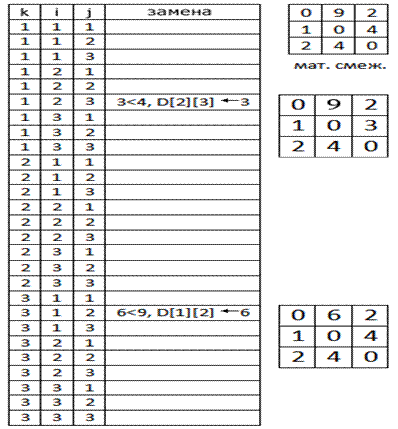
В данной таблице показаны 27 шагов выполнения основной части алгоритма. Их столько по той причине, что время выполнения метода равно O(|V|³). Наш граф имеет 3 вершины, а 3³=27. Первая замена происходит на итерации, при которой k=1, i=2, а j=3. В тот момент D[2][1]=1, D[1][3]=2, D[2][3]=4. Условие истинно, т. е. D[1][3]+D[3][2]=3, а 3<4, следовательно, элемент матрицы D[2][3] получает новое значение. Следующий шаг, когда условие также истинно привносит изменения в элемент, расположенный на пересечении второй строки и третьего столбца.

Список ребер

Список, в каждой строке которого записаны две смежные вершины и вес, соединяющего их ребра, называется списком ребер графа. Возьмем связный граф G=(V, E), и множество ребер E разделим на два класса d и k, где d – подмножество, включающее только неориентированные ребра графа G, а k – ориентированные. Предположим, что некоторая величина p соответствует количеству всех ребер, входящих в подмножество d, а s – тоже относительно k. Тогда для графа G высота списка ребер будет равна s+p*2. Иными словами, количество строк в списке ребер всегда должно быть равно величине, получающейся в результате сложения ориентированных ребер с неориентированными, увеличенными вдвое. Это утверждение следует из сказанного ранее, а именно, что данный способ представления графа предусматривает хранение в каждой строке двух смежных вершин, а неориентированное ребро, соединяющее вершины v и u, идет как из v в u, так и из u в v.

Рассмотрим смешанный граф, в котором 5 вершин, 4 ребра и каждому ребру поставлено в соответствие некоторое целое значение (для наглядности оно составлено из номеров вершин):

В нем 3 направленных ребра и 1 ненаправленное. Подставив значения в формулу, получим высоту списка ребер: 3+1*2=5.

Так выглядит список ребер для приведенного графа. Это таблица размером n×3, где n= s+p*2=3+1*2=5. Элементы первого столбца располагаются в порядке возрастания, в то время как порядок элементов второго столбца зависит от первого, а третьего от двух предыдущих.

Программная реализация списка ребер похожа на реализацию списка смежности. Так же как и в последней, в ней изначально необходимо организовать ввод данных, которые при помощи специальной функции будут распределяться по массивам. Второй шаг – вывести получившийся список смежности на экран.

В списке смежности хранились только смежные вершины, а здесь, помимо ни

12 Следующая ⇒

Воспользуйтесь поиском по сайту: